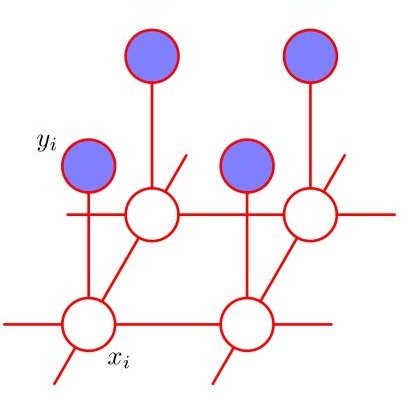
Generative models for learning combinatorial structures have transformative impacts in many applications. However, existing approaches fail to offer efficient and accurate learning results. Because of the highly intractable nature of the gradient estimation of the learning objective subject to combinatorial constraints. Existing gradient estimation methods would easily run into exponential time/memory space, or incur huge estimation errors due to improper approximation. We develop NEural Lovasz Sampler (Nelson), a neural network based on Lov\'asz Local Lemma (LLL). We show it guarantees to generate samples satisfying combinatorial constraints from the distribution of the constrained Markov Random Fields model (MRF) under certain conditions. We further present a fully differentiable contrastive-divergence-based learning framework on constrained MRF (Nelson-CD). Meanwhile, Nelson-CD being fully differentiable allows us to take advantage of the parallel computing power of GPUs, resulting in great efficiency. Experimental results on three real-world combinatorial problems reveal that Nelson learns to generate 100% valid structures. In comparison, baselines either time out on large-size data sets or fail to generate valid structures, whereas Nelson scales much better with problem size. In addition, Nelson outperforms baselines in various learning metrics, such as log-likelihood and MAP scores.
相關內容
In recent years, Reinforcement Learning (RL) has been applied to real-world problems with increasing success. Such applications often require to put constraints on the agent's behavior. Existing algorithms for constrained RL (CRL) rely on gradient descent-ascent, but this approach comes with a caveat. While these algorithms are guaranteed to converge on average, they do not guarantee last-iterate convergence, i.e., the current policy of the agent may never converge to the optimal solution. In practice, it is often observed that the policy alternates between satisfying the constraints and maximizing the reward, rarely accomplishing both objectives simultaneously. Here, we address this problem by introducing Reinforcement Learning with Optimistic Ascent-Descent (ReLOAD), a principled CRL method with guaranteed last-iterate convergence. We demonstrate its empirical effectiveness on a wide variety of CRL problems including discrete MDPs and continuous control. In the process we establish a benchmark of challenging CRL problems.
Many real-world systems can be described by mathematical formulas that are human-comprehensible, easy to analyze and can be helpful in explaining the system's behaviour. Symbolic regression is a method that generates nonlinear models from data in the form of analytic expressions. Historically, symbolic regression has been predominantly realized using genetic programming, a method that iteratively evolves a population of candidate solutions that are sampled by genetic operators crossover and mutation. This gradient-free evolutionary approach suffers from several deficiencies: it does not scale well with the number of variables and samples in the training data, models tend to grow in size and complexity without an adequate accuracy gain, and it is hard to fine-tune the inner model coefficients using just genetic operators. Recently, neural networks have been applied to learn the whole analytic formula, i.e., its structure as well as the coefficients, by means of gradient-based optimization algorithms. We propose a novel neural network-based symbolic regression method that constructs physically plausible models based on limited training data and prior knowledge about the system. The method employs an adaptive weighting scheme to effectively deal with multiple loss function terms and an epoch-wise learning process to reduce the chance of getting stuck in poor local optima. Furthermore, we propose a parameter-free method for choosing the model with the best interpolation and extrapolation performance out of all models generated through the whole learning process. We experimentally evaluate the approach on the TurtleBot 2 mobile robot, the magnetic manipulation system, the equivalent resistance of two resistors in parallel, and the anti-lock braking system. The results clearly show the potential of the method to find sparse and accurate models that comply with the prior knowledge provided.
Using gradient descent (GD) with fixed or decaying step-size is a standard practice in unconstrained optimization problems. However, when the loss function is only locally convex, such a step-size schedule artificially slows GD down as it cannot explore the flat curvature of the loss function. To overcome that issue, we propose to exponentially increase the step-size of the GD algorithm. Under homogeneous assumptions on the loss function, we demonstrate that the iterates of the proposed \emph{exponential step size gradient descent} (EGD) algorithm converge linearly to the optimal solution. Leveraging that optimization insight, we then consider using the EGD algorithm for solving parameter estimation under both regular and non-regular statistical models whose loss function becomes locally convex when the sample size goes to infinity. We demonstrate that the EGD iterates reach the final statistical radius within the true parameter after a logarithmic number of iterations, which is in stark contrast to a \emph{polynomial} number of iterations of the GD algorithm in non-regular statistical models. Therefore, the total computational complexity of the EGD algorithm is \emph{optimal} and exponentially cheaper than that of the GD for solving parameter estimation in non-regular statistical models while being comparable to that of the GD in regular statistical settings. To the best of our knowledge, it resolves a long-standing gap between statistical and algorithmic computational complexities of parameter estimation in non-regular statistical models. Finally, we provide targeted applications of the general theory to several classes of statistical models, including generalized linear models with polynomial link functions and location Gaussian mixture models.
Many existing reinforcement learning (RL) methods employ stochastic gradient iteration on the back end, whose stability hinges upon a hypothesis that the data-generating process mixes exponentially fast with a rate parameter that appears in the step-size selection. Unfortunately, this assumption is violated for large state spaces or settings with sparse rewards, and the mixing time is unknown, making the step size inoperable. In this work, we propose an RL methodology attuned to the mixing time by employing a multi-level Monte Carlo estimator for the critic, the actor, and the average reward embedded within an actor-critic (AC) algorithm. This method, which we call \textbf{M}ulti-level \textbf{A}ctor-\textbf{C}ritic (MAC), is developed especially for infinite-horizon average-reward settings and neither relies on oracle knowledge of the mixing time in its parameter selection nor assumes its exponential decay; it, therefore, is readily applicable to applications with slower mixing times. Nonetheless, it achieves a convergence rate comparable to the state-of-the-art AC algorithms. We experimentally show that these alleviated restrictions on the technical conditions required for stability translate to superior performance in practice for RL problems with sparse rewards.
Producing thousands of simulations of the dark matter distribution in the Universe with increasing precision is a challenging but critical task to facilitate the exploitation of current and forthcoming cosmological surveys. Many inexpensive substitutes to full $N$-body simulations have been proposed, even though they often fail to reproduce the statistics of the smaller, non-linear scales. Among these alternatives, a common approximation is represented by the lognormal distribution, which comes with its own limitations as well, while being extremely fast to compute even for high-resolution density fields. In this work, we train a generative deep learning model, mainly made of convolutional layers, to transform projected lognormal dark matter density fields to more realistic dark matter maps, as obtained from full $N$-body simulations. We detail the procedure that we follow to generate highly correlated pairs of lognormal and simulated maps, which we use as our training data, exploiting the information of the Fourier phases. We demonstrate the performance of our model comparing various statistical tests with different field resolutions, redshifts and cosmological parameters, proving its robustness and explaining its current limitations. When evaluated on 100 test maps, the augmented lognormal random fields reproduce the power spectrum up to wavenumbers of $1 \ h \ \rm{Mpc}^{-1}$, and the bispectrum within 10%, and always within the error bars, of the fiducial target simulations. Finally, we describe how we plan to integrate our proposed model with existing tools to yield more accurate spherical random fields for weak lensing analysis.
We consider the problem of learning a target function corresponding to a deep, extensive-width, non-linear neural network with random Gaussian weights. We consider the asymptotic limit where the number of samples, the input dimension and the network width are proportionally large. We derive a closed-form expression for the Bayes-optimal test error, for regression and classification tasks. We contrast these Bayes-optimal errors with the test errors of ridge regression, kernel and random features regression. We find, in particular, that optimally regularized ridge regression, as well as kernel regression, achieve Bayes-optimal performances, while the logistic loss yields a near-optimal test error for classification. We further show numerically that when the number of samples grows faster than the dimension, ridge and kernel methods become suboptimal, while neural networks achieve test error close to zero from quadratically many samples.
Computational chemistry has become an important tool to predict and understand molecular properties and reactions. Even though recent years have seen a significant growth in new algorithms and computational methods that speed up quantum chemical calculations, the bottleneck for trajectory-based methods to study photoinduced processes is still the huge number of electronic structure calculations. In this work, we present an innovative solution, in which the amount of electronic structure calculations is drastically reduced, by employing machine learning algorithms and methods borrowed from the realm of artificial intelligence. However, applying these algorithms effectively requires finding optimal hyperparameters, which remains a challenge itself. Here we present an automated user-friendly framework, HOAX, to perform the hyperparameter optimization for neural networks, which bypasses the need for a lengthy manual process. The neural network generated potential energy surfaces (PESs) reduces the computational costs compared to the ab initio-based PESs. We perform a comparative investigation on the performance of different hyperparameter optimiziation algorithms, namely grid search, simulated annealing, genetic algorithm, and bayesian optimizer in finding the optimal hyperparameters necessary for constructing the well-performing neural network in order to fit the PESs of small organic molecules. Our results show that this automated toolkit not only facilitate a straightforward way to perform the hyperparameter optimization but also the resulting neural networks-based generated PESs are in reasonable agreement with the ab initio-based PESs.
Offline model selection (OMS), that is, choosing the best policy from a set of many policies given only logged data, is crucial for applying offline RL in real-world settings. One idea that has been extensively explored is to select policies based on the mean squared Bellman error (MSBE) of the associated Q-functions. However, previous work has struggled to obtain adequate OMS performance with Bellman errors, leading many researchers to abandon the idea. Through theoretical and empirical analyses, we elucidate why previous work has seen pessimistic results with Bellman errors and identify conditions under which OMS algorithms based on Bellman errors will perform well. Moreover, we develop a new estimator of the MSBE that is more accurate than prior methods and obtains impressive OMS performance on diverse discrete control tasks, including Atari games. We open-source our data and code to enable researchers to conduct OMS experiments more easily.
Graph Neural Networks (GNNs), which generalize deep neural networks to graph-structured data, have drawn considerable attention and achieved state-of-the-art performance in numerous graph related tasks. However, existing GNN models mainly focus on designing graph convolution operations. The graph pooling (or downsampling) operations, that play an important role in learning hierarchical representations, are usually overlooked. In this paper, we propose a novel graph pooling operator, called Hierarchical Graph Pooling with Structure Learning (HGP-SL), which can be integrated into various graph neural network architectures. HGP-SL incorporates graph pooling and structure learning into a unified module to generate hierarchical representations of graphs. More specifically, the graph pooling operation adaptively selects a subset of nodes to form an induced subgraph for the subsequent layers. To preserve the integrity of graph's topological information, we further introduce a structure learning mechanism to learn a refined graph structure for the pooled graph at each layer. By combining HGP-SL operator with graph neural networks, we perform graph level representation learning with focus on graph classification task. Experimental results on six widely used benchmarks demonstrate the effectiveness of our proposed model.
Graph neural networks (GNNs) are a popular class of machine learning models whose major advantage is their ability to incorporate a sparse and discrete dependency structure between data points. Unfortunately, GNNs can only be used when such a graph-structure is available. In practice, however, real-world graphs are often noisy and incomplete or might not be available at all. With this work, we propose to jointly learn the graph structure and the parameters of graph convolutional networks (GCNs) by approximately solving a bilevel program that learns a discrete probability distribution on the edges of the graph. This allows one to apply GCNs not only in scenarios where the given graph is incomplete or corrupted but also in those where a graph is not available. We conduct a series of experiments that analyze the behavior of the proposed method and demonstrate that it outperforms related methods by a significant margin.