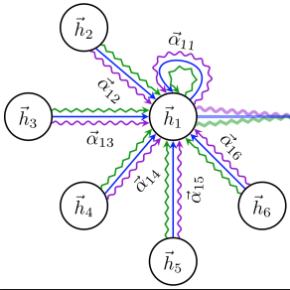
Oversmoothing in Graph Neural Networks (GNNs) refers to the phenomenon where increasing network depth leads to homogeneous node representations. While previous work has established that Graph Convolutional Networks (GCNs) exponentially lose expressive power, it remains controversial whether the graph attention mechanism can mitigate oversmoothing. In this work, we provide a definitive answer to this question through a rigorous mathematical analysis, by viewing attention-based GNNs as nonlinear time-varying dynamical systems and incorporating tools and techniques from the theory of products of inhomogeneous matrices and the joint spectral radius. We establish that, contrary to popular belief, the graph attention mechanism cannot prevent oversmoothing and loses expressive power exponentially. The proposed framework extends the existing results on oversmoothing for symmetric GCNs to a significantly broader class of GNN models, including random walk GCNs, Graph Attention Networks (GATs) and (graph) transformers. In particular, our analysis accounts for asymmetric, state-dependent and time-varying aggregation operators and a wide range of common nonlinear activation functions, such as ReLU, LeakyReLU, GELU and SiLU.
相關內容
Session types provide a typing discipline for message-passing systems. However, their theory often assumes an ideal world: one in which everything is reliable and without failures. Yet this is in stark contrast with distributed systems in the real world. To address this limitation, we introduce a new asynchronous multiparty session types (MPST) theory with crash-stop failures, where processes may crash arbitrarily and cease to interact after crashing. We augment asynchronous MPST and processes with crash handling branches, and integrate crash-stop failure semantics into types and processes. Our approach requires no user-level syntax extensions for global types, and features a formalisation of global semantics, which captures complex behaviours induced by crashed/crash handling processes. Our new theory covers the entire spectrum, ranging from the ideal world of total reliability to entirely unreliable scenarios where any process may crash, using optional reliability assumptions. Under these assumptions, we demonstrate the sound and complete correspondence between global and local type semantics, which guarantee deadlock-freedom, protocol conformance, and liveness of well-typed processes by construction, even in the presence of crashes.
We consider the movable antenna (MA) array-enabled wireless communication with coordinate multi-point (CoMP) reception, where multiple destinations adopt the maximal ratio combination technique to jointly decode the common message sent from the transmitter equipped with the MA array. Our goal is to maximize the effective received signal-to-noise ratio, by jointly optimizing the transmit beamforming and the positions of the MA array. Although the formulated problem is highly non-convex, we reveal that it is fundamental to maximize the principal eigenvalue of a hermite channel matrix which is a function of the positions of the MA array. The corresponding sub-problem is still non-convex, for which we develop a computationally efficient algorithm. Afterwards, the optimal transmit beamforming is determined with a closed-form solution. In addition, the theoretical performance upper bound is analyzed. Since the MA array brings an additional spatial degree of freedom by flexibly adjusting all antennas' positions, it achieves significant performance gain compared to competitive benchmarks.
We propose a new method, called a deep-genetic algorithm (deep-GA), to accelerate the performance of the so-called deep-BSDE method, which is a deep learning algorithm to solve high dimensional partial differential equations through their corresponding backward stochastic differential equations (BSDEs). Recognizing the sensitivity of the solver to the initial guess selection, we embed a genetic algorithm (GA) into the solver to optimize the selection. We aim to achieve faster convergence for the nonlinear PDEs on a broader interval than deep-BSDE. Our proposed method is applied to two nonlinear parabolic PDEs, i.e., the Black-Scholes (BS) equation with default risk and the Hamilton-Jacobi-Bellman (HJB) equation. We compare the results of our method with those of the deep-BSDE and show that our method provides comparable accuracy with significantly improved computational efficiency.
Determining the optimal fidelity for the transmission of quantum information over noisy quantum channels is one of the central problems in quantum information theory. Recently, [Berta-Borderi-Fawzi-Scholz, Mathematical Programming, 2021] introduced an asymptotically converging semidefinite programming hierarchy of outer bounds for this quantity. However, the size of the semidefinite programs (SDPs) grows exponentially with respect to the level of the hierarchy, thus making their computation unscalable. In this work, by exploiting the symmetries in the SDP, we show that, for fixed input and output dimensions of the given quantum channel, we can compute the SDP in polynomial time in terms of the level of the hierarchy. As a direct consequence of our result, the optimal fidelity can be approximated with an accuracy of $\epsilon$ in a time that is polynomial in $1/\epsilon$.
Decades of research indicate that emotion recognition is more effective when drawing information from multiple modalities. But what if some modalities are sometimes missing? To address this problem, we propose a novel Transformer-based architecture for recognizing valence and arousal in a time-continuous manner even with missing input modalities. We use a coupling of cross-attention and self-attention mechanisms to emphasize relationships between modalities during time and enhance the learning process on weak salient inputs. Experimental results on the Ulm-TSST dataset show that our model exhibits an improvement of the concordance correlation coefficient evaluation of 37% when predicting arousal values and 30% when predicting valence values, compared to a late-fusion baseline approach.
Backdoor (Trojan) attack is a common threat to deep neural networks, where samples from one or more source classes embedded with a backdoor trigger will be misclassified to adversarial target classes. Existing methods for detecting whether a classifier is backdoor attacked are mostly designed for attacks with a single adversarial target (e.g., all-to-one attack). To the best of our knowledge, without supervision, no existing methods can effectively address the more general X2X attack with an arbitrary number of source classes, each paired with an arbitrary target class. In this paper, we propose UMD, the first Unsupervised Model Detection method that effectively detects X2X backdoor attacks via a joint inference of the adversarial (source, target) class pairs. In particular, we first define a novel transferability statistic to measure and select a subset of putative backdoor class pairs based on a proposed clustering approach. Then, these selected class pairs are jointly assessed based on an aggregation of their reverse-engineered trigger size for detection inference, using a robust and unsupervised anomaly detector we proposed. We conduct comprehensive evaluations on CIFAR-10, GTSRB, and Imagenette dataset, and show that our unsupervised UMD outperforms SOTA detectors (even with supervision) by 17%, 4%, and 8%, respectively, in terms of the detection accuracy against diverse X2X attacks. We also show the strong detection performance of UMD against several strong adaptive attacks.
The notion of group invariance helps neural networks in recognizing patterns and features under geometric transformations. Indeed, it has been shown that group invariance can largely improve deep learning performances in practice, where such transformations are very common. This research studies affine invariance on continuous-domain convolutional neural networks. Despite other research considering isometric invariance or similarity invariance, we focus on the full structure of affine transforms generated by the generalized linear group $\mathrm{GL}_2(\mathbb{R})$. We introduce a new criterion to assess the similarity of two input signals under affine transformations. Then, unlike conventional methods that involve solving complex optimization problems on the Lie group $G_2$, we analyze the convolution of lifted signals and compute the corresponding integration over $G_2$. In sum, our research could eventually extend the scope of geometrical transformations that practical deep-learning pipelines can handle.
We consider the problem of explaining the predictions of graph neural networks (GNNs), which otherwise are considered as black boxes. Existing methods invariably focus on explaining the importance of graph nodes or edges but ignore the substructures of graphs, which are more intuitive and human-intelligible. In this work, we propose a novel method, known as SubgraphX, to explain GNNs by identifying important subgraphs. Given a trained GNN model and an input graph, our SubgraphX explains its predictions by efficiently exploring different subgraphs with Monte Carlo tree search. To make the tree search more effective, we propose to use Shapley values as a measure of subgraph importance, which can also capture the interactions among different subgraphs. To expedite computations, we propose efficient approximation schemes to compute Shapley values for graph data. Our work represents the first attempt to explain GNNs via identifying subgraphs explicitly and directly. Experimental results show that our SubgraphX achieves significantly improved explanations, while keeping computations at a reasonable level.
Graph Neural Networks (GNNs) have recently become increasingly popular due to their ability to learn complex systems of relations or interactions arising in a broad spectrum of problems ranging from biology and particle physics to social networks and recommendation systems. Despite the plethora of different models for deep learning on graphs, few approaches have been proposed thus far for dealing with graphs that present some sort of dynamic nature (e.g. evolving features or connectivity over time). In this paper, we present Temporal Graph Networks (TGNs), a generic, efficient framework for deep learning on dynamic graphs represented as sequences of timed events. Thanks to a novel combination of memory modules and graph-based operators, TGNs are able to significantly outperform previous approaches being at the same time more computationally efficient. We furthermore show that several previous models for learning on dynamic graphs can be cast as specific instances of our framework. We perform a detailed ablation study of different components of our framework and devise the best configuration that achieves state-of-the-art performance on several transductive and inductive prediction tasks for dynamic graphs.
We propose a novel single shot object detection network named Detection with Enriched Semantics (DES). Our motivation is to enrich the semantics of object detection features within a typical deep detector, by a semantic segmentation branch and a global activation module. The segmentation branch is supervised by weak segmentation ground-truth, i.e., no extra annotation is required. In conjunction with that, we employ a global activation module which learns relationship between channels and object classes in a self-supervised manner. Comprehensive experimental results on both PASCAL VOC and MS COCO detection datasets demonstrate the effectiveness of the proposed method. In particular, with a VGG16 based DES, we achieve an mAP of 81.7 on VOC2007 test and an mAP of 32.8 on COCO test-dev with an inference speed of 31.5 milliseconds per image on a Titan Xp GPU. With a lower resolution version, we achieve an mAP of 79.7 on VOC2007 with an inference speed of 13.0 milliseconds per image.