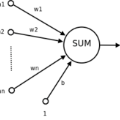
Partial differential equations have a wide range of applications in modeling multiple physical, biological, or social phenomena. Therefore, we need to approximate the solutions of these equations in computationally feasible terms. Nowadays, among the most popular numerical methods for solving partial differential equations in engineering, we encounter the finite difference and finite element methods. An alternative numerical method that has recently gained popularity for numerically solving partial differential equations is the use of artificial neural networks. Artificial neural networks, or neural networks for short, are mathematical structures with universal approximation properties. In addition, thanks to the extraordinary computational development of the last decade, neural networks have become accessible and powerful numerical methods for engineers and researchers. For example, imaging and language processing are applications of neural networks today that show sublime performance inconceivable years ago. This dissertation contributes to the numerical solution of partial differential equations using neural networks with the following two-fold objective: investigate the behavior of neural networks as approximators of solutions of partial differential equations and propose neural-network-based methods for frameworks that are hardly addressable via traditional numerical methods. As novel neural-network-based proposals, we first present a method inspired by the finite element method when applying mesh refinements to solve parametric problems. Secondly, we propose a general residual minimization scheme based on a generalized version of the Ritz method. Finally, we develop a memory-based strategy to overcome a usual numerical integration limitation when using neural networks to solve partial differential equations.
相關內容
ZX-diagrams are a powerful graphical language for the description of quantum processes with applications in fundamental quantum mechanics, quantum circuit optimization, tensor network simulation, and many more. The utility of ZX-diagrams relies on a set of local transformation rules that can be applied to them without changing the underlying quantum process they describe. These rules can be exploited to optimize the structure of ZX-diagrams for a range of applications. However, finding an optimal sequence of transformation rules is generally an open problem. In this work, we bring together ZX-diagrams with reinforcement learning, a machine learning technique designed to discover an optimal sequence of actions in a decision-making problem and show that a trained reinforcement learning agent can significantly outperform other optimization techniques like a greedy strategy or simulated annealing. The use of graph neural networks to encode the policy of the agent enables generalization to diagrams much bigger than seen during the training phase.
We develop a novel approach for efficiently applying variational quantum linear solver (VQLS) in context of structured sparse matrices. Such matrices frequently arise during numerical solution of partial differential equations which are ubiquitous in science and engineering. Conventionally, Pauli basis is used for linear combination of unitary (LCU) decomposition of the underlying matrix to facilitate the evaluation the global/local VQLS cost functions. However, Pauli basis in worst case can result in number of LCU terms that scale quadratically with respect to the matrix size. We show that by using an alternate basis one can better exploit the sparsity and underlying structure of matrix leading to number of tensor product terms which scale only logarithmically with respect to the matrix size. Given this new basis is comprised of non-unitary operators, we employ the concept of unitary completion to design efficient quantum circuits for computing the global/local VQLS cost functions. We compare our approach with other related concepts in the literature including unitary dilation and measurement in Bell basis, and discuss its pros/cons while using VQLS applied to Heat equation as an example.
An equation based reduced order model applicable to generalized heat equation and thermal simulations of power electronics systems developed in commercial CFD tools, is presented in this work. The model considers the physics of heat transfer between multiple objects in different mediums and presents a set of equations that can be applied to a wide range of heat transfer scenarios including conduction, natural and forced convection problems. A few case studies including heat transfer in a power electronic system are simulated in Ansys Icepak and the temperatures from the simulations are compared with the temperatures predicted by the models. The models are observed to be highly accurate when compared with the simulations. The predictive model described in this work reduces large complex simulations down to a few parameters which tremendously improves the computation speed, uses very low physical disk space and enables fast evaluation of thermal performance of the system for any changes in the input parameters.
The list-labeling problem is one of the most basic and well-studied algorithmic primitives in data structures, with an extensive literature spanning upper bounds, lower bounds, and data management applications. The classical algorithm for this problem, dating back to 1981, has amortized cost $O(\log^2 n)$. Subsequent work has led to improvements in three directions: \emph{low-latency} (worst-case) bounds; \emph{high-throughput} (expected) bounds; and (adaptive) bounds for \emph{important workloads}. Perhaps surprisingly, these three directions of research have remained almost entirely disjoint -- this is because, so far, the techniques that allow for progress in one direction have forced worsening bounds in the others. Thus there would appear to be a tension between worst-case, adaptive, and expected bounds. List labeling has been proposed for use in databases at least as early as PODS'99, but a database needs good throughput, response time, and needs to adapt to common workloads (e.g., bulk loads), and no current list-labeling algorithm achieve good bounds for all three. We show that this tension is not fundamental. In fact, with the help of new data-structural techniques, one can actually \emph{combine} any three list-labeling solutions in order to cherry-pick the best worst-case, adaptive, and expected bounds from each of them.
For robustness toward model misspecification, the generalized posterior inference approach modifies the likelihood term by raising it to the power of a learning rate, thereby adjusting the spread of the posterior. This paper proposes a computationally efficient strategy for selecting an appropriate learning rate. The proposed approach builds upon the generalized posterior calibration (GPC) algorithm introduced by Syring and Martin (2019) [Biometrika, Volume 106, Issue 2, pp. 479-486], which is designed to select the learning rate to achieve the nominal frequentist coverage. This algorithm, which evaluates the coverage probability based on bootstrap samples, suffers from high computational costs due to the need for repeated posterior simulations for bootstrap samples. To address this limitation, the study proposes an algorithm that combines elements of the GPC algorithm with the sequential Monte Carlo (SMC) sampler. By leveraging the similarity between the learning rate in generalized posterior inference and the inverse temperature in SMC sampling, the proposed algorithm efficiently calibrates the posterior distribution with less computational cost. For demonstration, the proposed algorithm was applied to several statistical learning models.
It is shown how to efficiently and accurately compute and optimize a range of cross validation criteria for a wide range of models estimated by minimizing a quadratically penalized smooth loss. Example models include generalized additive models for location scale and shape and smooth additive quantile regression. Example losses include negative log likelihoods and smooth quantile losses. Example cross validation criteria include leave-out-neighbourhood cross validation for dealing with un-modelled short range autocorrelation as well as the more familiar leave-one-out cross validation. For a $p$ coefficient model of $n$ data, estimable at $O(np^2)$ computational cost, the general $O(n^2p^2)$ cost of ordinary cross validation is reduced to $O(np^2)$, computing the cross validation criterion to $O(p^3n^{-2})$ accuracy. This is achieved by directly approximating the model coefficient estimates under data subset omission, via efficiently computed single step Newton updates of the full data coefficient estimates. Optimization of the resulting cross validation criterion, with respect to multiple smoothing/precision parameters, can be achieved efficiently using quasi-Newton optimization, adapted to deal with the indefiniteness that occurs when the optimal value for a smoothing parameter tends to infinity. The link between cross validation and the jackknife can be exploited to achieve reasonably well calibrated uncertainty quantification for the model coefficients in non standard settings such as leaving-out-neighbourhoods under residual autocorrelation or quantile regression. Several practical examples are provided, focussing particularly on dealing with un-modelled auto-correlation.
In many real-world applications where the system dynamics has an underlying interdependency among its variables (such as power grid, economics, neuroscience, omics networks, environmental ecosystems, and others), one is often interested in knowing whether the past values of one time series influences the future of another, known as Granger causality, and the associated underlying dynamics. This paper introduces a Koopman-inspired framework that leverages neural networks for data-driven learning of the Koopman bases, termed NeuroKoopman Dynamic Causal Discovery (NKDCD), for reliably inferring the Granger causality along with the underlying nonlinear dynamics. NKDCD employs an autoencoder architecture that lifts the nonlinear dynamics to a higher dimension using data-learned bases, where the lifted time series can be reliably modeled linearly. The lifting function, the linear Granger causality lag matrices, and the projection function (from lifted space to base space) are all represented as multilayer perceptrons and are all learned simultaneously in one go. NKDCD also utilizes sparsity-inducing penalties on the weights of the lag matrices, encouraging the model to select only the needed causal dependencies within the data. Through extensive testing on practically applicable datasets, it is shown that the NKDCD outperforms the existing nonlinear Granger causality discovery approaches.
Given a causal graph representing the data-generating process shared across different domains/distributions, enforcing sufficient graph-implied conditional independencies can identify domain-general (non-spurious) feature representations. For the standard input-output predictive setting, we categorize the set of graphs considered in the literature into two distinct groups: (i) those in which the empirical risk minimizer across training domains gives domain-general representations and (ii) those where it does not. For the latter case (ii), we propose a novel framework with regularizations, which we demonstrate are sufficient for identifying domain-general feature representations without a priori knowledge (or proxies) of the spurious features. Empirically, our proposed method is effective for both (semi) synthetic and real-world data, outperforming other state-of-the-art methods in average and worst-domain transfer accuracy.
Unsupervised clustering of wafer map defect patterns is challenging because the appearance of certain defect patterns varies significantly. This includes changing shape, location, density, and rotation of the defect area on the wafer. We present a harvesting approach, which can cluster even challenging defect patterns of wafer maps well. Our approach makes use of a well-known, three-step procedure: feature extraction, dimension reduction, and clustering. The novelty in our approach lies in repeating dimensionality reduction and clustering iteratively while filtering out one cluster per iteration according to its silhouette score. This method leads to an improvement of clustering performance in general and is especially useful for difficult defect patterns. The low computational effort allows for a quick assessment of large datasets and can be used to support manual labeling efforts. We benchmark against related approaches from the literature and show improved results on a real-world industrial dataset.
The dominant sequence transduction models are based on complex recurrent or convolutional neural networks in an encoder-decoder configuration. The best performing models also connect the encoder and decoder through an attention mechanism. We propose a new simple network architecture, the Transformer, based solely on attention mechanisms, dispensing with recurrence and convolutions entirely. Experiments on two machine translation tasks show these models to be superior in quality while being more parallelizable and requiring significantly less time to train. Our model achieves 28.4 BLEU on the WMT 2014 English-to-German translation task, improving over the existing best results, including ensembles by over 2 BLEU. On the WMT 2014 English-to-French translation task, our model establishes a new single-model state-of-the-art BLEU score of 41.8 after training for 3.5 days on eight GPUs, a small fraction of the training costs of the best models from the literature. We show that the Transformer generalizes well to other tasks by applying it successfully to English constituency parsing both with large and limited training data.