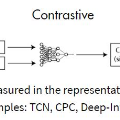
In response to an object presentation, supervised learning schemes generally respond with a parsimonious label. Upon a similar presentation we humans respond again with a label, but are flooded, in addition, by a myriad of associations. A significant portion of these consist of the presented object attributes. Contrastive learning is a semi-supervised learning scheme based on the application of identity preserving transformations on the object input representations. It is conjectured in this work that these same applied transformations preserve, in addition to the identity of the presented object, also the identity of its semantically meaningful attributes. The corollary of this is that the output representations of such a contrastive learning scheme contain valuable information not only for the classification of the presented object, but also for the presence or absence decision of any attribute of interest. Simulation results which demonstrate this idea and the feasibility of this conjecture are presented.
相關內容
We present a computational formulation for the approximate version of several variational inequality problems, investigating their computational complexity and establishing PPAD-completeness. Examining applications in computational game theory, we specifically focus on two key concepts: resilient Nash equilibrium, and multi-leader-follower games -- domains traditionally known for the absence of general solutions. In the presence of standard assumptions and relaxation techniques, we formulate problem versions for such games that are expressible in terms of variational inequalities, ultimately leading to proofs of PPAD-completeness.
Symmetries are prevalent in deep learning and can significantly influence the learning dynamics of neural networks. In this paper, we examine how exponential symmetries -- a broad subclass of continuous symmetries present in the model architecture or loss function -- interplay with stochastic gradient descent (SGD). We first prove that gradient noise creates a systematic motion (a ``Noether flow") of the parameters $\theta$ along the degenerate direction to a unique initialization-independent fixed point $\theta^*$. These points are referred to as the {\it noise equilibria} because, at these points, noise contributions from different directions are balanced and aligned. Then, we show that the balance and alignment of gradient noise can serve as a novel alternative mechanism for explaining important phenomena such as progressive sharpening/flattening and representation formation within neural networks and have practical implications for understanding techniques like representation normalization and warmup.
We put forth Oblivious State Preparation (OSP) as a cryptographic primitive that unifies techniques developed in the context of a quantum server interacting with a classical client. OSP allows a classical polynomial-time sender to input a choice of one out of two public observables, and a quantum polynomial-time receiver to recover an eigenstate of the corresponding observable -- while keeping the sender's choice hidden from any malicious receiver. We obtain the following results: - The existence of (plain) trapdoor claw-free functions implies OSP, and the existence of dual-mode trapdoor claw-free functions implies round-optimal (two-round) OSP. - OSP implies the existence of proofs of quantumness, test of a qubit, blind classical delegation of quantum computation, and classical verification of quantum computation. - Two-round OSP implies quantum money with classical communication, classically-verifiable position verification, and (additionally assuming classical FHE with log-depth decryption) quantum FHE. Several of these applications were previously only known via tailored LWE-based constructions, whereas our OSP-based constructions yield new results from a wider variety of assumptions, including hard problems on cryptographic group actions. Finally, towards understanding the minimal hardness assumptions required to realize OSP, we prove the following: - OSP implies oblivious transfer between one classical and one quantum party. - Two-round OSP implies public-key encryption with classical keys and ciphertexts. In particular, these results help to ''explain'' the use of public-key cryptography in the known approaches to establishing a ''classical leash'' on a quantum server. For example, combined with a result of Austrin et al. (CRYPTO 22), we conclude that perfectly-correct OSP cannot exist unconditionally in the (quantum) random oracle model.
The Holant theorem is a powerful tool for studying the computational complexity of counting problems in the Holant framework. Due to the great expressiveness of the Holant framework, a converse to the Holant theorem would itself be a very powerful counting indistinguishability theorem. The most general converse does not hold, but we prove the following, still highly general, version: if any two sets of real-valued signatures are Holant-indistinguishable, then they are equivalent up to an orthogonal transformation. This resolves a partially open conjecture of Xia (2010). Consequences of this theorem include the well-known result that homomorphism counts from all graphs determine a graph up to isomorphism, the classical sufficient condition for simultaneous orthogonal similarity of sets of real matrices, and a combinatorial characterization of simultaneosly orthogonally decomposable (odeco) sets of symmetric tensors.
All machine learning algorithms use a loss, cost, utility or reward function to encode the learning objective and oversee the learning process. This function that supervises learning is a frequently unrecognized hyperparameter that determines how incorrect outputs are penalized and can be tuned to improve performance. This paper shows that training speed and final accuracy of neural networks can significantly depend on the loss function used to train neural networks. In particular derivative values can be significantly different with different loss functions leading to significantly different performance after gradient descent based Backpropagation (BP) training. This paper explores the effect on performance of using new loss functions that are also convex but penalize errors differently compared to the popular Cross-entropy loss. Two new classification loss functions that significantly improve performance on a wide variety of benchmark tasks are proposed. A new loss function call smooth absolute error that outperforms the Squared error, Huber and Log-Cosh losses on datasets with significantly many outliers is proposed. This smooth absolute error loss function is infinitely differentiable and more closely approximates the absolute error loss compared to the Huber and Log-Cosh losses used for robust regression.
We investigate the patterns of incorrect answers produced by large language models (LLMs) during evaluation. These errors exhibit highly non-intuitive behaviors unique to each model. By analyzing these patterns, we measure the similarities between LLMs and construct a taxonomy that categorizes them based on their error correlations. Our findings reveal that the incorrect responses are not randomly distributed but systematically correlated across models, providing new insights into the underlying structures and relationships among LLMs.
Self-supervised learning, dubbed the dark matter of intelligence, is a promising path to advance machine learning. Yet, much like cooking, training SSL methods is a delicate art with a high barrier to entry. While many components are familiar, successfully training a SSL method involves a dizzying set of choices from the pretext tasks to training hyper-parameters. Our goal is to lower the barrier to entry into SSL research by laying the foundations and latest SSL recipes in the style of a cookbook. We hope to empower the curious researcher to navigate the terrain of methods, understand the role of the various knobs, and gain the know-how required to explore how delicious SSL can be.
Pre-trained Language Models (PLMs) which are trained on large text corpus via self-supervised learning method, have yielded promising performance on various tasks in Natural Language Processing (NLP). However, though PLMs with huge parameters can effectively possess rich knowledge learned from massive training text and benefit downstream tasks at the fine-tuning stage, they still have some limitations such as poor reasoning ability due to the lack of external knowledge. Research has been dedicated to incorporating knowledge into PLMs to tackle these issues. In this paper, we present a comprehensive review of Knowledge-Enhanced Pre-trained Language Models (KE-PLMs) to provide a clear insight into this thriving field. We introduce appropriate taxonomies respectively for Natural Language Understanding (NLU) and Natural Language Generation (NLG) to highlight these two main tasks of NLP. For NLU, we divide the types of knowledge into four categories: linguistic knowledge, text knowledge, knowledge graph (KG), and rule knowledge. The KE-PLMs for NLG are categorized into KG-based and retrieval-based methods. Finally, we point out some promising future directions of KE-PLMs.

AI is undergoing a paradigm shift with the rise of models (e.g., BERT, DALL-E, GPT-3) that are trained on broad data at scale and are adaptable to a wide range of downstream tasks. We call these models foundation models to underscore their critically central yet incomplete character. This report provides a thorough account of the opportunities and risks of foundation models, ranging from their capabilities (e.g., language, vision, robotics, reasoning, human interaction) and technical principles(e.g., model architectures, training procedures, data, systems, security, evaluation, theory) to their applications (e.g., law, healthcare, education) and societal impact (e.g., inequity, misuse, economic and environmental impact, legal and ethical considerations). Though foundation models are based on standard deep learning and transfer learning, their scale results in new emergent capabilities,and their effectiveness across so many tasks incentivizes homogenization. Homogenization provides powerful leverage but demands caution, as the defects of the foundation model are inherited by all the adapted models downstream. Despite the impending widespread deployment of foundation models, we currently lack a clear understanding of how they work, when they fail, and what they are even capable of due to their emergent properties. To tackle these questions, we believe much of the critical research on foundation models will require deep interdisciplinary collaboration commensurate with their fundamentally sociotechnical nature.
Neural machine translation (NMT) is a deep learning based approach for machine translation, which yields the state-of-the-art translation performance in scenarios where large-scale parallel corpora are available. Although the high-quality and domain-specific translation is crucial in the real world, domain-specific corpora are usually scarce or nonexistent, and thus vanilla NMT performs poorly in such scenarios. Domain adaptation that leverages both out-of-domain parallel corpora as well as monolingual corpora for in-domain translation, is very important for domain-specific translation. In this paper, we give a comprehensive survey of the state-of-the-art domain adaptation techniques for NMT.