This paper introduces a new fundamental characteristic, \ie, the dynamic range, from real-world metric tools to deep visual recognition. In metrology, the dynamic range is a basic quality of a metric tool, indicating its flexibility to accommodate various scales. Larger dynamic range offers higher flexibility. In visual recognition, the multiple scale problem also exist. Different visual concepts may have different semantic scales. For example, ``Animal'' and ``Plants'' have a large semantic scale while ``Elk'' has a much smaller one. Under a small semantic scale, two different elks may look quite \emph{different} to each other . However, under a large semantic scale (\eg, animals and plants), these two elks should be measured as being \emph{similar}. %We argue that such flexibility is also important for deep metric learning, because different visual concepts indeed correspond to different semantic scales. Introducing the dynamic range to deep metric learning, we get a novel computer vision task, \ie, the Dynamic Metric Learning. It aims to learn a scalable metric space to accommodate visual concepts across multiple semantic scales. Based on three types of images, \emph{i.e.}, vehicle, animal and online products, we construct three datasets for Dynamic Metric Learning. We benchmark these datasets with popular deep metric learning methods and find Dynamic Metric Learning to be very challenging. The major difficulty lies in a conflict between different scales: the discriminative ability under a small scale usually compromises the discriminative ability under a large one, and vice versa. As a minor contribution, we propose Cross-Scale Learning (CSL) to alleviate such conflict. We show that CSL consistently improves the baseline on all the three datasets. The datasets and the code will be publicly available at //github.com/SupetZYK/DynamicMetricLearning.
相關內容
Supervised and semi-supervised learning methods have been traditionally designed for the closed-world setting based on the assumption that unlabeled test data contains only classes previously encountered in the labeled training data. However, the real world is inherently open and dynamic, and thus novel, previously unseen classes may appear in the test data or during the model deployment. Here, we introduce a new open-world semi-supervised learning setting in which the model is required to recognize previously seen classes, as well as to discover novel classes never seen in the labeled dataset. To tackle the problem, we propose ORCA, an approach that learns to simultaneously classify and cluster the data. ORCA classifies examples from the unlabeled dataset to previously seen classes, or forms a novel class by grouping similar examples together. The key idea in ORCA is in introducing uncertainty based adaptive margin that effectively circumvents the bias caused by the imbalance of variance between seen and novel classes/clusters. We demonstrate that ORCA accurately discovers novel classes and assigns samples to previously seen classes on benchmark image classification datasets, including CIFAR and ImageNet. Remarkably, despite solving the harder task ORCA outperforms semi-supervised methods on seen classes, as well as novel class discovery methods on novel classes, achieving 7% and 151% improvements on seen and novel classes in the ImageNet dataset.
This paper presents a hardness-aware deep metric learning (HDML) framework. Most previous deep metric learning methods employ the hard negative mining strategy to alleviate the lack of informative samples for training. However, this mining strategy only utilizes a subset of training data, which may not be enough to characterize the global geometry of the embedding space comprehensively. To address this problem, we perform linear interpolation on embeddings to adaptively manipulate their hard levels and generate corresponding label-preserving synthetics for recycled training, so that information buried in all samples can be fully exploited and the metric is always challenged with proper difficulty. Our method achieves very competitive performance on the widely used CUB-200-2011, Cars196, and Stanford Online Products datasets.
Few-shot Learning aims to learn classifiers for new classes with only a few training examples per class. Existing meta-learning or metric-learning based few-shot learning approaches are limited in handling diverse domains with various number of labels. The meta-learning approaches train a meta learner to predict weights of homogeneous-structured task-specific networks, requiring a uniform number of classes across tasks. The metric-learning approaches learn one task-invariant metric for all the tasks, and they fail if the tasks diverge. We propose to deal with these limitations with meta metric learning. Our meta metric learning approach consists of task-specific learners, that exploit metric learning to handle flexible labels, and a meta learner, that discovers good parameters and gradient decent to specify the metrics in task-specific learners. Thus the proposed model is able to handle unbalanced classes as well as to generate task-specific metrics. We test our approach in the `$k$-shot $N$-way' few-shot learning setting used in previous work and new realistic few-shot setting with diverse multi-domain tasks and flexible label numbers. Experiments show that our approach attains superior performances in both settings.
Representation learning for networks provides a new way to mine graphs. Although current researches in this area are able to generate reliable results of node embeddings, they are still limited to homogeneous networks in which all nodes and edges are of the same type. While, increasingly, graphs are heterogeneous with multiple node- and edge- types in the real world. Existing heterogeneous embedding methods are mostly task-based or only able to deal with limited types of node & edge. To tackle this challenge, in this paper, an edge2vec model is proposed to represent nodes in ways that incorporate edge semantics represented as different edge-types in heterogeneous networks. An edge-type transition matrix is optimized from an Expectation-Maximization (EM) framework as an extra criterion of a biased node random walk on networks, and a biased skip-gram model is leveraged to learn node embeddings based on the random walks afterwards. edge2vec is validated and evaluated using three medical domain problems on an ensemble of complex medical networks (more than 10 node- \& edge- types): medical entity classification, compound-gene binding prediction, and medical information searching cost. Results show that by considering edge semantics, edge2vec significantly outperforms other state-of-art models on all three tasks.
Tracking by detection is a common approach to solving the Multiple Object Tracking problem. In this paper we show how deep metric learning can be used to improve three aspects of tracking by detection. We train a convolutional neural network to learn an embedding function in a Siamese configuration on a large person re-identification dataset offline. It is then used to improve the online performance of tracking while retaining a high frame rate. We use this learned appearance metric to robustly build estimates of pedestrian's trajectories in the MOT16 dataset. In breaking with the tracking by detection model, we use our appearance metric to propose detections using the predicted state of a tracklet as a prior in the case where the detector fails. This method achieves competitive results in evaluation, especially among online, real-time approaches. We present an ablative study showing the impact of each of the three uses of our deep appearance metric.
Deep learning is the mainstream technique for many machine learning tasks, including image recognition, machine translation, speech recognition, and so on. It has outperformed conventional methods in various fields and achieved great successes. Unfortunately, the understanding on how it works remains unclear. It has the central importance to lay down the theoretic foundation for deep learning. In this work, we give a geometric view to understand deep learning: we show that the fundamental principle attributing to the success is the manifold structure in data, namely natural high dimensional data concentrates close to a low-dimensional manifold, deep learning learns the manifold and the probability distribution on it. We further introduce the concepts of rectified linear complexity for deep neural network measuring its learning capability, rectified linear complexity of an embedding manifold describing the difficulty to be learned. Then we show for any deep neural network with fixed architecture, there exists a manifold that cannot be learned by the network. Finally, we propose to apply optimal mass transportation theory to control the probability distribution in the latent space.
Metric learning learns a metric function from training data to calculate the similarity or distance between samples. From the perspective of feature learning, metric learning essentially learns a new feature space by feature transformation (e.g., Mahalanobis distance metric). However, traditional metric learning algorithms are shallow, which just learn one metric space (feature transformation). Can we further learn a better metric space from the learnt metric space? In other words, can we learn metric progressively and nonlinearly like deep learning by just using the existing metric learning algorithms? To this end, we present a hierarchical metric learning scheme and implement an online deep metric learning framework, namely ODML. Specifically, we take one online metric learning algorithm as a metric layer, followed by a nonlinear layer (i.e., ReLU), and then stack these layers modelled after the deep learning. The proposed ODML enjoys some nice properties, indeed can learn metric progressively and performs superiorly on some datasets. Various experiments with different settings have been conducted to verify these properties of the proposed ODML.
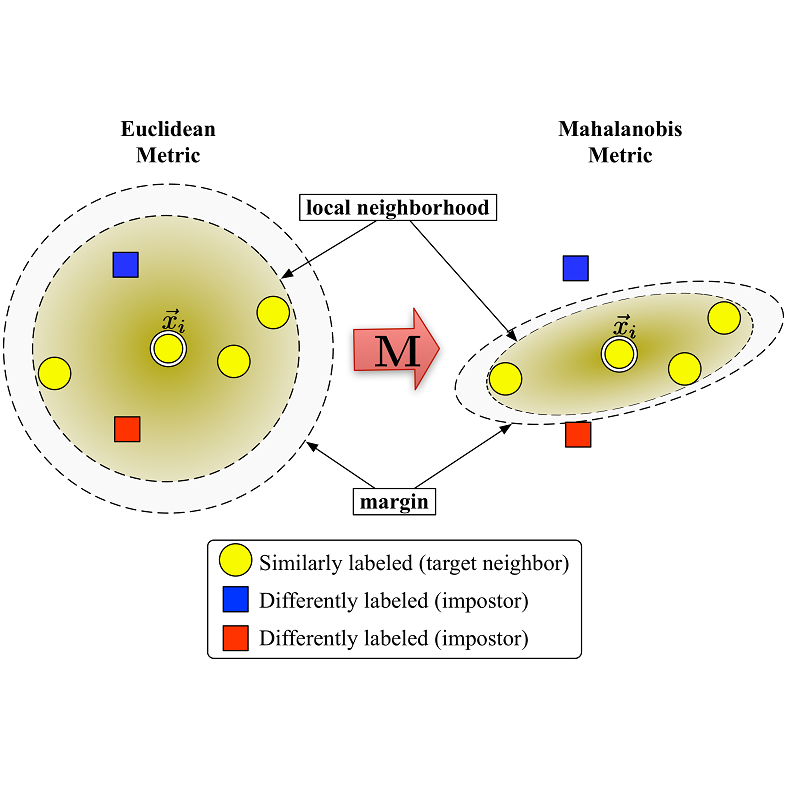
Large margin nearest neighbor (LMNN) is a metric learner which optimizes the performance of the popular $k$NN classifier. However, its resulting metric relies on pre-selected target neighbors. In this paper, we address the feasibility of LMNN's optimization constraints regarding these target points, and introduce a mathematical measure to evaluate the size of the feasible region of the optimization problem. We enhance the optimization framework of LMNN by a weighting scheme which prefers data triplets which yield a larger feasible region. This increases the chances to obtain a good metric as the solution of LMNN's problem. We evaluate the performance of the resulting feasibility-based LMNN algorithm using synthetic and real datasets. The empirical results show an improved accuracy for different types of datasets in comparison to regular LMNN.
Recently, ensemble has been applied to deep metric learning to yield state-of-the-art results. Deep metric learning aims to learn deep neural networks for feature embeddings, distances of which satisfy given constraint. In deep metric learning, ensemble takes average of distances learned by multiple learners. As one important aspect of ensemble, the learners should be diverse in their feature embeddings. To this end, we propose an attention-based ensemble, which uses multiple attention masks, so that each learner can attend to different parts of the object. We also propose a divergence loss, which encourages diversity among the learners. The proposed method is applied to the standard benchmarks of deep metric learning and experimental results show that it outperforms the state-of-the-art methods by a significant margin on image retrieval tasks.
Collecting training data from the physical world is usually time-consuming and even dangerous for fragile robots, and thus, recent advances in robot learning advocate the use of simulators as the training platform. Unfortunately, the reality gap between synthetic and real visual data prohibits direct migration of the models trained in virtual worlds to the real world. This paper proposes a modular architecture for tackling the virtual-to-real problem. The proposed architecture separates the learning model into a perception module and a control policy module, and uses semantic image segmentation as the meta representation for relating these two modules. The perception module translates the perceived RGB image to semantic image segmentation. The control policy module is implemented as a deep reinforcement learning agent, which performs actions based on the translated image segmentation. Our architecture is evaluated in an obstacle avoidance task and a target following task. Experimental results show that our architecture significantly outperforms all of the baseline methods in both virtual and real environments, and demonstrates a faster learning curve than them. We also present a detailed analysis for a variety of variant configurations, and validate the transferability of our modular architecture.