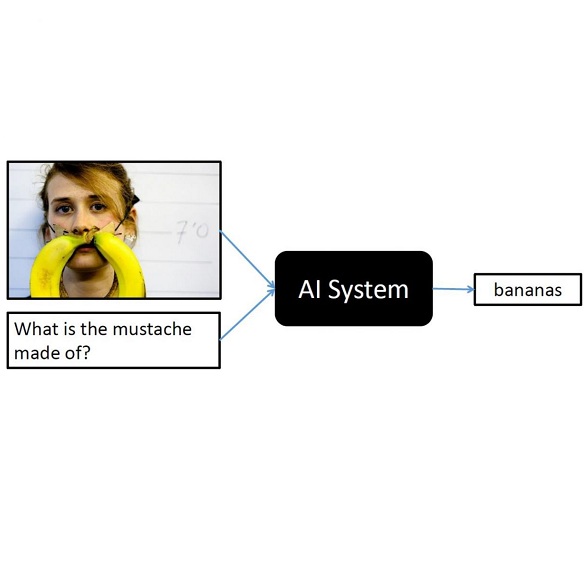
The various limitations of Generative AI, such as hallucinations and model failures, have made it crucial to understand the role of different modalities in Visual Language Model (VLM) predictions. Our work investigates how the integration of information from image and text modalities influences the performance and behavior of VLMs in visual question answering (VQA) and reasoning tasks. We measure this effect through answer accuracy, reasoning quality, model uncertainty, and modality relevance. We study the interplay between text and image modalities in different configurations where visual content is essential for solving the VQA task. Our contributions include (1) the Semantic Interventions (SI)-VQA dataset, (2) a benchmark study of various VLM architectures under different modality configurations, and (3) the Interactive Semantic Interventions (ISI) tool. The SI-VQA dataset serves as the foundation for the benchmark, while the ISI tool provides an interface to test and apply semantic interventions in image and text inputs, enabling more fine-grained analysis. Our results show that complementary information between modalities improves answer and reasoning quality, while contradictory information harms model performance and confidence. Image text annotations have minimal impact on accuracy and uncertainty, slightly increasing image relevance. Attention analysis confirms the dominant role of image inputs over text in VQA tasks. In this study, we evaluate state-of-the-art VLMs that allow us to extract attention coefficients for each modality. A key finding is PaliGemma's harmful overconfidence, which poses a higher risk of silent failures compared to the LLaVA models. This work sets the foundation for rigorous analysis of modality integration, supported by datasets specifically designed for this purpose.
相關內容
Uncertainty Quantification (UQ) is crucial for reliable image segmentation. Yet, while the field sees continual development of novel methods, a lack of agreed-upon benchmarks limits their systematic comparison and evaluation: Current UQ methods are typically tested either on overly simplistic toy datasets or on complex real-world datasets that do not allow to discern true uncertainty. To unify both controllability and complexity, we introduce Arctique, a procedurally generated dataset modeled after histopathological colon images. We chose histopathological images for two reasons: 1) their complexity in terms of intricate object structures and highly variable appearance, which yields challenging segmentation problems, and 2) their broad prevalence for medical diagnosis and respective relevance of high-quality UQ. To generate Arctique, we established a Blender-based framework for 3D scene creation with intrinsic noise manipulation. Arctique contains 50,000 rendered images with precise masks as well as noisy label simulations. We show that by independently controlling the uncertainty in both images and labels, we can effectively study the performance of several commonly used UQ methods. Hence, Arctique serves as a critical resource for benchmarking and advancing UQ techniques and other methodologies in complex, multi-object environments, bridging the gap between realism and controllability. All code is publicly available, allowing re-creation and controlled manipulations of our shipped images as well as creation and rendering of new scenes.
A statistical framework we call CQUESST (Carbon Quantification and Uncertainty from Evolutionary Soil STochastics), which models carbon sequestration and cycling in soils, is applied to a long-running agricultural experiment that controls for crop type, tillage, and season. The experiment, known as the Millenium Tillage Trial (MTT), ran on 42 field-plots for ten years from 2000-2010; here CQUESST is used to model soil carbon dynamically in six pools, in each of the 42 agricultural plots, and on a monthly time step for a decade. We show how CQUESST can be used to estimate soil-carbon cycling rates under different treatments. Our methods provide much-needed statistical tools for quantitatively inferring the effectiveness of different experimental treatments on soil-carbon sequestration. The decade-long data are of multiple observation types, and these interacting time series are ingested into a fully Bayesian model that has a dynamic stochastic model of multiple pools of soil carbon at its core. CQUESST's stochastic model is motivated by the deterministic RothC soil-carbon model based on nonlinear difference equations. We demonstrate how CQUESST can estimate soil-carbon fluxes for different experimental treatments while acknowledging uncertainties in soil-carbon dynamics, in physical parameters, and in observations. CQUESST is implemented efficiently in the probabilistic programming language Stan using its MapReduce parallelization, and it scales well for large numbers of field-plots, using software libraries that allow for computation to be shared over multiple nodes of high-performance computing clusters.
Deep Learning-based Reduced Order Models (DL-ROMs) provide nowadays a well-established class of accurate surrogate models for complex physical systems described by parametrized PDEs, by nonlinearly compressing the solution manifold into a handful of latent coordinates. Until now, design and application of DL-ROMs mainly focused on physically parameterized problems. Within this work, we provide a novel extension of these architectures to problems featuring geometrical variability and parametrized domains, namely, we propose Continuous Geometry-Aware DL-ROMs (CGA-DL-ROMs). In particular, the space-continuous nature of the proposed architecture matches the need to deal with multi-resolution datasets, which are quite common in the case of geometrically parametrized problems. Moreover, CGA-DL-ROMs are endowed with a strong inductive bias that makes them aware of geometrical parametrizations, thus enhancing both the compression capability and the overall performance of the architecture. Within this work, we justify our findings through a thorough theoretical analysis, and we practically validate our claims by means of a series of numerical tests encompassing physically-and-geometrically parametrized PDEs, ranging from the unsteady Navier-Stokes equations for fluid dynamics to advection-diffusion-reaction equations for mathematical biology.
We provide abstract, general and highly uniform rates of asymptotic regularity for a generalized stochastic Halpern-style iteration, which incorporates a second mapping in the style of a Krasnoselskii-Mann iteration. This iteration is general in two ways: First, it incorporates stochasticity in a completely abstract way rather than fixing a sampling method; secondly, it includes as special cases stochastic versions of various schemes from the optimization literature, including Halpern's iteration as well as a Krasnoselskii-Mann iteration with Tikhonov regularization terms in the sense of Bo\c{t}, Csetnek and Meier. For these particular cases, we in particular obtain linear rates of asymptotic regularity, matching (or improving) the currently best known rates for these iterations in stochastic optimization, and quadratic rates of asymptotic regularity are obtained in the context of inner product spaces for the general iteration. We utilize these rates to give bounds on the oracle complexity of such iterations under suitable variance assumptions and batching strategies, again presented in an abstract style. Finally, we sketch how the schemes presented here can be instantiated in the context of reinforcement learning to yield novel methods for Q-learning.
We consider the problem of sampling a high dimensional multimodal target probability measure. We assume that a good proposal kernel to move only a subset of the degrees of freedoms (also known as collective variables) is known a priori. This proposal kernel can for example be built using normalizing flows. We show how to extend the move from the collective variable space to the full space and how to implement an accept-reject step in order to get a reversible chain with respect to a target probability measure. The accept-reject step does not require to know the marginal of the original measure in the collective variable (namely to know the free energy). The obtained algorithm admits several variants, some of them being very close to methods which have been proposed previously in the literature. We show how the obtained acceptance ratio can be expressed in terms of the work which appears in the Jarzynski-Crooks equality, at least for some variants. Numerical illustrations demonstrate the efficiency of the approach on various simple test cases, and allow us to compare the variants of the algorithm.
Machine learning in production needs to balance multiple objectives: This is particularly evident in ranking or recommendation models, where conflicting objectives such as user engagement, satisfaction, diversity, and novelty must be considered at the same time. However, designing multi-objective rankers is inherently a dynamic wicked problem -- there is no single optimal solution, and the needs evolve over time. Effective design requires collaboration between cross-functional teams and careful analysis of a wide range of information. In this work, we introduce Orbit, a conceptual framework for Objective-centric Ranker Building and Iteration. The framework places objectives at the center of the design process, to serve as boundary objects for communication and guide practitioners for design and evaluation. We implement Orbit as an interactive system, which enables stakeholders to interact with objective spaces directly and supports real-time exploration and evaluation of design trade-offs. We evaluate Orbit through a user study involving twelve industry practitioners, showing that it supports efficient design space exploration, leads to more informed decision-making, and enhances awareness of the inherent trade-offs of multiple objectives. Orbit (1) opens up new opportunities of an objective-centric design process for any multi-objective ML models, as well as (2) sheds light on future designs that push practitioners to go beyond a narrow metric-centric or example-centric mindset.
In decision-making, maxitive functions are used for worst-case and best-case evaluations. Maxitivity gives rise to a rich structure that is well-studied in the context of the pointwise order. In this article, we investigate maxitivity with respect to general preorders and provide a representation theorem for such functionals. The results are illustrated for different stochastic orders in the literature, including the usual stochastic order, the increasing convex/concave order, and the dispersive order.
The Johnson--Lindenstrauss (JL) lemma is a powerful tool for dimensionality reduction in modern algorithm design. The lemma states that any set of high-dimensional points in a Euclidean space can be flattened to lower dimensions while approximately preserving pairwise Euclidean distances. Random matrices satisfying this lemma are called JL transforms (JLTs). Inspired by existing $s$-hashing JLTs with exactly $s$ nonzero elements on each column, the present work introduces an ensemble of sparse matrices encompassing so-called $s$-hashing-like matrices whose expected number of nonzero elements on each column is~$s$. The independence of the sub-Gaussian entries of these matrices and the knowledge of their exact distribution play an important role in their analyses. Using properties of independent sub-Gaussian random variables, these matrices are demonstrated to be JLTs, and their smallest and largest singular values are estimated non-asymptotically using a technique from geometric functional analysis. As the dimensions of the matrix grow to infinity, these singular values are proved to converge almost surely to fixed quantities (by using the universal Bai--Yin law), and in distribution to the Gaussian orthogonal ensemble (GOE) Tracy--Widom law after proper rescalings. Understanding the behaviors of extreme singular values is important in general because they are often used to define a measure of stability of matrix algorithms. For example, JLTs were recently used in derivative-free optimization algorithmic frameworks to select random subspaces in which are constructed random models or poll directions to achieve scalability, whence estimating their smallest singular value in particular helps determine the dimension of these subspaces.
We consider linear models with scalar responses and covariates from a separable Hilbert space. The aim is to detect change points in the error distribution, based on sequential residual empirical distribution functions. Expansions for those estimated functions are more challenging in models with infinite-dimensional covariates than in regression models with scalar or vector-valued covariates due to a slower rate of convergence of the parameter estimators. Yet the suggested change point test is asymptotically distribution-free and consistent for one-change point alternatives. In the latter case we also show consistency of a change point estimator.
We present SimpleQA, a benchmark that evaluates the ability of language models to answer short, fact-seeking questions. We prioritized two properties in designing this eval. First, SimpleQA is challenging, as it is adversarially collected against GPT-4 responses. Second, responses are easy to grade, because questions are created such that there exists only a single, indisputable answer. Each answer in SimpleQA is graded as either correct, incorrect, or not attempted. A model with ideal behavior would get as many questions correct as possible while not attempting the questions for which it is not confident it knows the correct answer. SimpleQA is a simple, targeted evaluation for whether models "know what they know," and our hope is that this benchmark will remain relevant for the next few generations of frontier models. SimpleQA can be found at //github.com/openai/simple-evals.