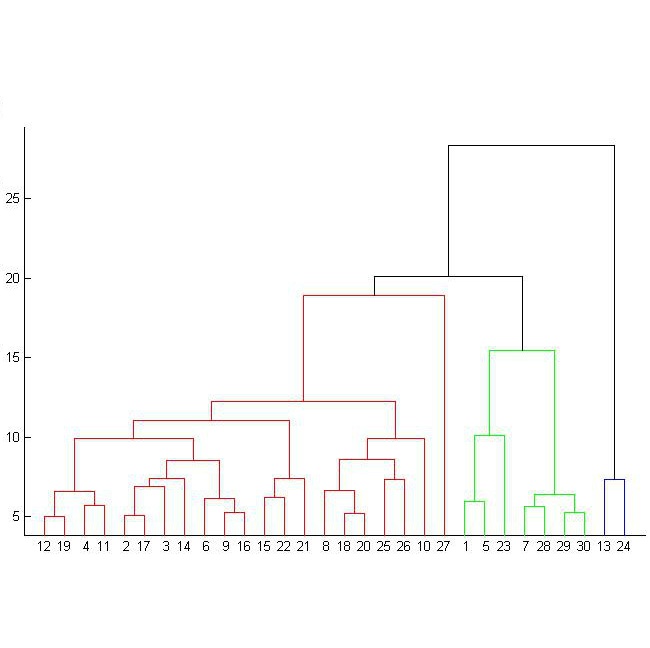
In this article, we define a new non-archimedean metric structure, called cophenetic metric, on persistent homology classes of all degrees. We then show that zeroth persistent homology together with the cophenetic metric and hierarchical clustering algorithms with a number of different metrics do deliver statistically verifiable commensurate topological information based on experimental results we obtained on different datasets. We also observe that the resulting clusters coming from cophenetic distance do shine in terms of different evaluation measures such as silhouette score and the Rand index. Moreover, since the cophenetic metric is defined for all homology degrees, one can now display the inter-relations of persistent homology classes in all degrees via rooted trees.
相關內容
Let $G=(V,E)$ be an undirected unweighted planar graph. Consider a vector storing the distances from an arbitrary vertex $v$ to all vertices $S = \{ s_1 , s_2 , \ldots , s_k \}$ of a single face in their cyclic order. The pattern of $v$ is obtained by taking the difference between every pair of consecutive values of this vector. In STOC'19, Li and Parter used a VC-dimension argument to show that in planar graphs, the number of distinct patterns, denoted $x$, is only $O(k^3)$. This resulted in a simple compression scheme requiring $\tilde O(\min \{ k^4+|T|, k\cdot |T|\})$ space to encode the distances between $S$ and a subset of terminal vertices $T \subseteq V$. This is known as the Okamura-Seymour metric compression problem. We give an alternative proof of the $x=O(k^3)$ bound that exploits planarity beyond the VC-dimension argument. Namely, our proof relies on cut-cycle duality, as well as on the fact that distances among vertices of $S$ are bounded by $k$. Our method implies the following: (1) An $\tilde{O}(x+k+|T|)$ space compression of the Okamura-Seymour metric, thus improving the compression of Li and Parter to $\tilde O(\min \{k^3+|T|,k \cdot |T| \})$. (2) An optimal $\tilde{O}(k+|T|)$ space compression of the Okamura-Seymour metric, in the case where the vertices of $T$ induce a connected component in $G$. (3) A tight bound of $x = \Theta(k^2)$ for the family of Halin graphs, whereas the VC-dimension argument is limited to showing $x=O(k^3)$.
In Machine Learning, a benchmark refers to an ensemble of datasets associated with one or multiple metrics together with a way to aggregate different systems performances. They are instrumental in (i) assessing the progress of new methods along different axes and (ii) selecting the best systems for practical use. This is particularly the case for NLP with the development of large pre-trained models (e.g. GPT, BERT) that are expected to generalize well on a variety of tasks. While the community mainly focused on developing new datasets and metrics, there has been little interest in the aggregation procedure, which is often reduced to a simple average over various performance measures. However, this procedure can be problematic when the metrics are on a different scale, which may lead to spurious conclusions. This paper proposes a new procedure to rank systems based on their performance across different tasks. Motivated by the social choice theory, the final system ordering is obtained through aggregating the rankings induced by each task and is theoretically grounded. We conduct extensive numerical experiments (on over 270k scores) to assess the soundness of our approach both on synthetic and real scores (e.g. GLUE, EXTREM, SEVAL, TAC, FLICKR). In particular, we show that our method yields different conclusions on state-of-the-art systems than the mean-aggregation procedure while being both more reliable and robust.
We investigate the large-sample behavior of change-point tests based on weighted two-sample U-statistics, in the case of short-range dependent data. Under some mild mixing conditions, we establish convergence of the test statistic to an extreme value distribution. A simulation study shows that the weighted tests are superior to the non-weighted versions when the change-point occurs near the boundary of the time interval, while they loose power in the center.
We present a list decoding algorithm for quaternary negacyclic codes over the Lee metric. To achieve this result, we use a Sudan-Guruswami type list decoding algorithm for Reed-Solomon codes over certain ring alphabets. Our decoding strategy for negacyclic codes over the ring $\mathbb Z_4$ combines the list decoding algorithm by Wu with the Gr\"obner basis approach for solving a key equation due to Byrne and Fitzpatrick.
We study timed systems in which some timing features are unknown parameters. Parametric timed automata (PTAs) are a classical formalism for such systems but for which most interesting problems are undecidable. Notably, the parametric reachability emptiness problem, i.e., the emptiness of the parameter valuations set allowing to reach some given discrete state, is undecidable. Lower-bound/upper-bound parametric timed automata (L/U-PTAs) achieve decidability for reachability properties by enforcing a separation of parameters used as upper bounds in the automaton constraints, and those used as lower bounds. In this paper, we first study reachability. We exhibit a subclass of PTAs (namely integer-points PTAs) with bounded rational-valued parameters for which the parametric reachability emptiness problem is decidable. Using this class, we present further results improving the boundary between decidability and undecidability for PTAs and their subclasses such as L/U-PTAs. We then study liveness. We prove that: (1) deciding the existence of at least one parameter valuation for which there exists an infinite run in an L/U-PTA is PSpace-complete; (2) the existence of a parameter valuation such that the system has a deadlock is however undecidable; (3) the problem of the existence of a valuation for which a run remains in a given set of locations exhibits a very thin border between decidability and undecidability.
We consider the problem of discovering $K$ related Gaussian directed acyclic graphs (DAGs), where the involved graph structures share a consistent causal order and sparse unions of supports. Under the multi-task learning setting, we propose a $l_1/l_2$-regularized maximum likelihood estimator (MLE) for learning $K$ linear structural equation models. We theoretically show that the joint estimator, by leveraging data across related tasks, can achieve a better sample complexity for recovering the causal order (or topological order) than separate estimations. Moreover, the joint estimator is able to recover non-identifiable DAGs, by estimating them together with some identifiable DAGs. Lastly, our analysis also shows the consistency of union support recovery of the structures. To allow practical implementation, we design a continuous optimization problem whose optimizer is the same as the joint estimator and can be approximated efficiently by an iterative algorithm. We validate the theoretical analysis and the effectiveness of the joint estimator in experiments.
This work focuses on combining nonparametric topic models with Auto-Encoding Variational Bayes (AEVB). Specifically, we first propose iTM-VAE, where the topics are treated as trainable parameters and the document-specific topic proportions are obtained by a stick-breaking construction. The inference of iTM-VAE is modeled by neural networks such that it can be computed in a simple feed-forward manner. We also describe how to introduce a hyper-prior into iTM-VAE so as to model the uncertainty of the prior parameter. Actually, the hyper-prior technique is quite general and we show that it can be applied to other AEVB based models to alleviate the {\it collapse-to-prior} problem elegantly. Moreover, we also propose HiTM-VAE, where the document-specific topic distributions are generated in a hierarchical manner. HiTM-VAE is even more flexible and can generate topic distributions with better variability. Experimental results on 20News and Reuters RCV1-V2 datasets show that the proposed models outperform the state-of-the-art baselines significantly. The advantages of the hyper-prior technique and the hierarchical model construction are also confirmed by experiments.
In this paper, we propose a nonlinear distance metric learning scheme based on the fusion of component linear metrics. Instead of merging displacements at each data point, our model calculates the velocities induced by the component transformations, via a geodesic interpolation on a Lie transfor- mation group. Such velocities are later summed up to produce a global transformation that is guaranteed to be diffeomorphic. Consequently, pair-wise distances computed this way conform to a smooth and spatially varying metric, which can greatly benefit k-NN classification. Experiments on synthetic and real datasets demonstrate the effectiveness of our model.
Metric learning learns a metric function from training data to calculate the similarity or distance between samples. From the perspective of feature learning, metric learning essentially learns a new feature space by feature transformation (e.g., Mahalanobis distance metric). However, traditional metric learning algorithms are shallow, which just learn one metric space (feature transformation). Can we further learn a better metric space from the learnt metric space? In other words, can we learn metric progressively and nonlinearly like deep learning by just using the existing metric learning algorithms? To this end, we present a hierarchical metric learning scheme and implement an online deep metric learning framework, namely ODML. Specifically, we take one online metric learning algorithm as a metric layer, followed by a nonlinear layer (i.e., ReLU), and then stack these layers modelled after the deep learning. The proposed ODML enjoys some nice properties, indeed can learn metric progressively and performs superiorly on some datasets. Various experiments with different settings have been conducted to verify these properties of the proposed ODML.
We present an implementation of a probabilistic first-order logic called TensorLog, in which classes of logical queries are compiled into differentiable functions in a neural-network infrastructure such as Tensorflow or Theano. This leads to a close integration of probabilistic logical reasoning with deep-learning infrastructure: in particular, it enables high-performance deep learning frameworks to be used for tuning the parameters of a probabilistic logic. Experimental results show that TensorLog scales to problems involving hundreds of thousands of knowledge-base triples and tens of thousands of examples.