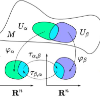
Given a real, finite-dimensional, smooth parallelizable Riemannian manifold $(\mathcal{N},G)$ endowed with a teleparallel connection $\nabla$ determined by a choice of a global basis of vector fields on $\mathcal{N}$, we show that the $G$-dual connection $\nabla^{*}$ of $\nabla$ in the sense of Information Geometry must be the teleparallel connection determined by the basis of $G$-gradient vector fields associated with a basis of differential one-forms which is (almost) dual to the basis of vector fields determining $\nabla$. We call any such pair $(\nabla,\nabla^{*})$ a $G$-dual teleparallel pair. Then, after defining a covariant $(0,3)$ tensor $T$ uniquely determined by $(\mathcal{N},G,\nabla,\nabla^{*})$, we show that $T$ being symmetric in the first two entries is equivalent to $\nabla$ being torsion-free, that $T$ being symmetric in the first and third entry is equivalent to $\nabla^{*}$ being torsion free, and that $T$ being symmetric in the second and third entries is equivalent to the basis vectors determining $\nabla$ ($\nabla^{*}$) being parallel-transported by $\nabla^{*}$ ($\nabla$). Therefore, $G$-dual teleparallel pairs provide a generalization of the notion of Statistical Manifolds usually employed in Information Geometry, and we present explicit examples of $G$-dual teleparallel pairs arising both in the context of both Classical and Quantum Information Geometry.
相關內容
We introduce the extremal range, a local statistic for studying the spatial extent of extreme events in random fields on $\mathbb{R}^2$. Conditioned on exceedance of a high threshold at a location $s$, the extremal range at $s$ is the random variable defined as the smallest distance from $s$ to a location where there is a non-exceedance. We leverage tools from excursion-set theory to study distributional properties of the extremal range, propose parametric models and predict the median extremal range at extreme threshold levels. The extremal range captures the rate at which the spatial extent of conditional extreme events scales for increasingly high thresholds, and we relate its distributional properties with the bivariate tail dependence coefficient and the extremal index of time series in classical Extreme-Value Theory. Consistent estimation of the distribution function of the extremal range for stationary random fields is proven. For non-stationary random fields, we implement generalized additive median regression to predict extremal-range maps at very high threshold levels. An application to two large daily temperature datasets, namely reanalyses and climate-model simulations for France, highlights decreasing extremal dependence for increasing threshold levels and reveals strong differences in joint tail decay rates between reanalyses and simulations.
We provide a generic construction to turn any classical Zero-Knowledge (ZK) protocol into a composable (quantum) oblivious transfer (OT) protocol, mostly lifting the round-complexity properties and security guarantees (plain-model/statistical security/unstructured functions...) of the ZK protocol to the resulting OT protocol. Such a construction is unlikely to exist classically as Cryptomania is believed to be different from Minicrypt. In particular, by instantiating our construction using Non-Interactive ZK (NIZK), we provide the first round-optimal (2-message) quantum OT protocol secure in the random oracle model, and round-optimal extensions to string and k-out-of-n OT. At the heart of our construction lies a new method that allows us to prove properties on a received quantum state without revealing additional information on it, even in a non-interactive way, without public-key primitives, and/or with statistical guarantees when using an appropriate classical ZK protocol. We can notably prove that a state has been partially measured (with arbitrary constraints on the set of measured qubits), without revealing any additional information on this set. This notion can be seen as an analog of ZK to quantum states, and we expect it to be of independent interest as it extends complexity theory to quantum languages, as illustrated by the two new complexity classes we introduce, ZKstatesQIP and ZKstatesQMA.
We consider the variable selection problem for two-sample tests, aiming to select the most informative variables to distinguish samples from two groups. To solve this problem, we propose a framework based on the kernel maximum mean discrepancy (MMD). Our approach seeks a group of variables with a pre-specified size that maximizes the variance-regularized MMD statistics. This formulation also corresponds to the minimization of asymptotic type-II error while controlling type-I error, as studied in the literature. We present mixed-integer programming formulations and develop exact and approximation algorithms with performance guarantees for different choices of kernel functions. Furthermore, we provide a statistical testing power analysis of our proposed framework. Experiment results on synthetic and real datasets demonstrate the superior performance of our approach.
We introduce a neural-preconditioned iterative solver for Poisson equations with mixed boundary conditions. The Poisson equation is ubiquitous in scientific computing: it governs a wide array of physical phenomena, arises as a subproblem in many numerical algorithms, and serves as a model problem for the broader class of elliptic PDEs. The most popular Poisson discretizations yield large sparse linear systems. At high resolution, and for performance-critical applications, iterative solvers can be advantageous for these -- but only when paired with powerful preconditioners. The core of our solver is a neural network trained to approximate the inverse of a discrete structured-grid Laplace operator for a domain of arbitrary shape and with mixed boundary conditions. The structure of this problem motivates a novel network architecture that we demonstrate is highly effective as a preconditioner even for boundary conditions outside the training set. We show that on challenging test cases arising from an incompressible fluid simulation, our method outperforms state-of-the-art solvers like algebraic multigrid as well as some recent neural preconditioners.
This study proposes an interpretable neural network-based non-proportional odds model (N$^3$POM) for ordinal regression. N$^3$POM is different from conventional approaches to ordinal regression with non-proportional models in several ways: (1) N$^3$POM is designed to directly handle continuous responses, whereas standard methods typically treat de facto ordered continuous variables as discrete, (2) instead of estimating response-dependent finite coefficients of linear models from discrete responses as is done in conventional approaches, we train a non-linear neural network to serve as a coefficient function. Thanks to the neural network, N$^3$POM offers flexibility while preserving the interpretability of conventional ordinal regression. We establish a sufficient condition under which the predicted conditional cumulative probability locally satisfies the monotonicity constraint over a user-specified region in the covariate space. Additionally, we provide a monotonicity-preserving stochastic (MPS) algorithm for effectively training the neural network. We apply N$^3$POM to several real-world datasets.
We study the problem of adaptive variable selection in a Gaussian white noise model of intensity $\varepsilon$ under certain sparsity and regularity conditions on an unknown regression function $f$. The $d$-variate regression function $f$ is assumed to be a sum of functions each depending on a smaller number $k$ of variables ($1 \leq k \leq d$). These functions are unknown to us and only few of them are non-zero. We assume that $d=d_\varepsilon \to \infty$ as $\varepsilon \to 0$ and consider the cases when $k$ is fixed and when $k=k_\varepsilon \to \infty$ and $k=o(d)$ as $\varepsilon \to 0$. In this work, we introduce an adaptive selection procedure that, under some model assumptions, identifies exactly all non-zero $k$-variate components of $f$. In addition, we establish conditions under which exact identification of the non-zero components is impossible. These conditions ensure that the proposed selection procedure is the best possible in the asymptotically minimax sense with respect to the Hamming risk.
Considerable effort has been dedicated to mitigating toxicity, but existing methods often require drastic modifications to model parameters or the use of computationally intensive auxiliary models. Furthermore, previous approaches have often neglected the crucial factor of language's evolving nature over time. In this work, we present a comprehensive perspective on toxicity mitigation that takes into account its changing nature. We introduce Goodtriever, a flexible methodology that matches the current state-of-the-art toxicity mitigation while achieving 43% relative latency reduction during inference and being more computationally efficient. By incorporating a retrieval-based approach at decoding time, Goodtriever enables toxicity-controlled text generation. Our research advocates for an increased focus on adaptable mitigation techniques, which better reflect the data drift models face when deployed in the wild. Code and data are available at //github.com/for-ai/goodtriever.
We consider the problem of discovering $K$ related Gaussian directed acyclic graphs (DAGs), where the involved graph structures share a consistent causal order and sparse unions of supports. Under the multi-task learning setting, we propose a $l_1/l_2$-regularized maximum likelihood estimator (MLE) for learning $K$ linear structural equation models. We theoretically show that the joint estimator, by leveraging data across related tasks, can achieve a better sample complexity for recovering the causal order (or topological order) than separate estimations. Moreover, the joint estimator is able to recover non-identifiable DAGs, by estimating them together with some identifiable DAGs. Lastly, our analysis also shows the consistency of union support recovery of the structures. To allow practical implementation, we design a continuous optimization problem whose optimizer is the same as the joint estimator and can be approximated efficiently by an iterative algorithm. We validate the theoretical analysis and the effectiveness of the joint estimator in experiments.
Conventional entity typing approaches are based on independent classification paradigms, which make them difficult to recognize inter-dependent, long-tailed and fine-grained entity types. In this paper, we argue that the implicitly entailed extrinsic and intrinsic dependencies between labels can provide critical knowledge to tackle the above challenges. To this end, we propose \emph{Label Reasoning Network(LRN)}, which sequentially reasons fine-grained entity labels by discovering and exploiting label dependencies knowledge entailed in the data. Specifically, LRN utilizes an auto-regressive network to conduct deductive reasoning and a bipartite attribute graph to conduct inductive reasoning between labels, which can effectively model, learn and reason complex label dependencies in a sequence-to-set, end-to-end manner. Experiments show that LRN achieves the state-of-the-art performance on standard ultra fine-grained entity typing benchmarks, and can also resolve the long tail label problem effectively.
Due to their inherent capability in semantic alignment of aspects and their context words, attention mechanism and Convolutional Neural Networks (CNNs) are widely applied for aspect-based sentiment classification. However, these models lack a mechanism to account for relevant syntactical constraints and long-range word dependencies, and hence may mistakenly recognize syntactically irrelevant contextual words as clues for judging aspect sentiment. To tackle this problem, we propose to build a Graph Convolutional Network (GCN) over the dependency tree of a sentence to exploit syntactical information and word dependencies. Based on it, a novel aspect-specific sentiment classification framework is raised. Experiments on three benchmarking collections illustrate that our proposed model has comparable effectiveness to a range of state-of-the-art models, and further demonstrate that both syntactical information and long-range word dependencies are properly captured by the graph convolution structure.