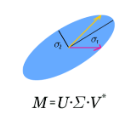
Several studies have shown the ability of natural gradient descent to minimize the objective function more efficiently than ordinary gradient descent based methods. However, the bottleneck of this approach for training deep neural networks lies in the prohibitive cost of solving a large dense linear system corresponding to the Fisher Information Matrix (FIM) at each iteration. This has motivated various approximations of either the exact FIM or the empirical one. The most sophisticated of these is KFAC, which involves a Kronecker-factored block diagonal approximation of the FIM. With only a slight additional cost, a few improvements of KFAC from the standpoint of accuracy are proposed. The common feature of the four novel methods is that they rely on a direct minimization problem, the solution of which can be computed via the Kronecker product singular value decomposition technique. Experimental results on the three standard deep auto-encoder benchmarks showed that they provide more accurate approximations to the FIM. Furthermore, they outperform KFAC and state-of-the-art first-order methods in terms of optimization speed.
相關內容
Graph Convolutional Networks (GCNs) are one of the most popular architectures that are used to solve classification problems accompanied by graphical information. We present a rigorous theoretical understanding of the effects of graph convolutions in multi-layer networks. We study these effects through the node classification problem of a non-linearly separable Gaussian mixture model coupled with a stochastic block model. First, we show that a single graph convolution expands the regime of the distance between the means where multi-layer networks can classify the data by a factor of at least $1/\sqrt[4]{\mathbb{E}{\rm deg}}$, where $\mathbb{E}{\rm deg}$ denotes the expected degree of a node. Second, we show that with a slightly stronger graph density, two graph convolutions improve this factor to at least $1/\sqrt[4]{n}$, where $n$ is the number of nodes in the graph. Finally, we provide both theoretical and empirical insights into the performance of graph convolutions placed in different combinations among the layers of a network, concluding that the performance is mutually similar for all combinations of the placement. We present extensive experiments on both synthetic and real-world data that illustrate our results.
We provide a decision theoretic analysis of bandit experiments. The setting corresponds to a dynamic programming problem, but solving this directly is typically infeasible. Working within the framework of diffusion asymptotics, we define suitable notions of asymptotic Bayes and minimax risk for bandit experiments. For normally distributed rewards, the minimal Bayes risk can be characterized as the solution to a nonlinear second-order partial differential equation (PDE). Using a limit of experiments approach, we show that this PDE characterization also holds asymptotically under both parametric and non-parametric distribution of the rewards. The approach further describes the state variables it is asymptotically sufficient to restrict attention to, and therefore suggests a practical strategy for dimension reduction. The upshot is that we can approximate the dynamic programming problem defining the bandit experiment with a PDE which can be efficiently solved using sparse matrix routines. We derive the optimal Bayes and minimax policies from the numerical solutions to these equations. The proposed policies substantially dominate existing methods such as Thompson sampling. The framework also allows for substantial generalizations to the bandit problem such as time discounting and pure exploration motives.
In the storied Colonel Blotto game, two colonels allocate $a$ and $b$ troops, respectively, to $k$ distinct battlefields. A colonel wins a battle if they assign more troops to that particular battle, and each colonel seeks to maximize their total number of victories. Despite the problem's formulation in 1921, the first polynomial-time algorithm to compute Nash equilibrium (NE) strategies for this game was discovered only quite recently. In 2016, \citep{ahmadinejad_dehghani_hajiaghayi_lucier_mahini_seddighin_2019} formulated a breakthrough algorithm to compute NE strategies for the Colonel Blotto game\footnote{To the best of our knowledge, the algorithm from \citep{ahmadinejad_dehghani_hajiaghayi_lucier_mahini_seddighin_2019} has computational complexity $O(k^{14}\max\{a,b\}^{13})$}, receiving substantial media coverage (e.g. \citep{Insider}, \citep{NSF}, \citep{ScienceDaily}). In this work, we present the first known $\epsilon$-approximation algorithm to compute NE strategies in the two-player Colonel Blotto game in runtime $\widetilde{O}(\epsilon^{-4} k^8 \max\{a,b\}^2)$ for arbitrary settings of these parameters. Moreover, this algorithm computes approximate coarse correlated equilibrium strategies in the multiplayer (continuous and discrete) Colonel Blotto game (when there are $\ell > 2$ colonels) with runtime $\widetilde{O}(\ell \epsilon^{-4} k^8 n^2 + \ell^2 \epsilon^{-2} k^3 n (n+k))$, where $n$ is the maximum troop count. Before this work, no polynomial-time algorithm was known to compute exact or approximate equilibrium (in any sense) strategies for multiplayer Colonel Blotto with arbitrary parameters. Our algorithm computes these approximate equilibria by a novel (to the author's knowledge) sampling technique with which we implicitly perform multiplicative weights update over the exponentially many strategies available to each player.
A High-dimensional and sparse (HiDS) matrix is frequently encountered in a big data-related application like an e-commerce system or a social network services system. To perform highly accurate representation learning on it is of great significance owing to the great desire of extracting latent knowledge and patterns from it. Latent factor analysis (LFA), which represents an HiDS matrix by learning the low-rank embeddings based on its observed entries only, is one of the most effective and efficient approaches to this issue. However, most existing LFA-based models perform such embeddings on a HiDS matrix directly without exploiting its hidden graph structures, thereby resulting in accuracy loss. To address this issue, this paper proposes a graph-incorporated latent factor analysis (GLFA) model. It adopts two-fold ideas: 1) a graph is constructed for identifying the hidden high-order interaction (HOI) among nodes described by an HiDS matrix, and 2) a recurrent LFA structure is carefully designed with the incorporation of HOI, thereby improving the representa-tion learning ability of a resultant model. Experimental results on three real-world datasets demonstrate that GLFA outperforms six state-of-the-art models in predicting the missing data of an HiDS matrix, which evidently supports its strong representation learning ability to HiDS data.
Low-rank matrix estimation under heavy-tailed noise is challenging, both computationally and statistically. Convex approaches have been proven statistically optimal but suffer from high computational costs, especially since robust loss functions are usually non-smooth. More recently, computationally fast non-convex approaches via sub-gradient descent are proposed, which, unfortunately, fail to deliver a statistically consistent estimator even under sub-Gaussian noise. In this paper, we introduce a novel Riemannian sub-gradient (RsGrad) algorithm which is not only computationally efficient with linear convergence but also is statistically optimal, be the noise Gaussian or heavy-tailed. Convergence theory is established for a general framework and specific applications to absolute loss, Huber loss, and quantile loss are investigated. Compared with existing non-convex methods, ours reveals a surprising phenomenon of dual-phase convergence. In phase one, RsGrad behaves as in a typical non-smooth optimization that requires gradually decaying stepsizes. However, phase one only delivers a statistically sub-optimal estimator which is already observed in the existing literature. Interestingly, during phase two, RsGrad converges linearly as if minimizing a smooth and strongly convex objective function and thus a constant stepsize suffices. Underlying the phase-two convergence is the smoothing effect of random noise to the non-smooth robust losses in an area close but not too close to the truth. Lastly, RsGrad is applicable for low-rank tensor estimation under heavy-tailed noise where a statistically optimal rate is attainable with the same phenomenon of dual-phase convergence, and a novel shrinkage-based second-order moment method is guaranteed to deliver a warm initialization. Numerical simulations confirm our theoretical discovery and showcase the superiority of RsGrad over prior methods.
One of the most important problems in system identification and statistics is how to estimate the unknown parameters of a given model. Optimization methods and specialized procedures, such as Empirical Minimization (EM) can be used in case the likelihood function can be computed. For situations where one can only simulate from a parametric model, but the likelihood is difficult or impossible to evaluate, a technique known as the Two-Stage (TS) Approach can be applied to obtain reliable parametric estimates. Unfortunately, there is currently a lack of theoretical justification for TS. In this paper, we propose a statistical decision-theoretical derivation of TS, which leads to Bayesian and Minimax estimators. We also show how to apply the TS approach on models for independent and identically distributed samples, by computing quantiles of the data as a first step, and using a linear function as the second stage. The proposed method is illustrated via numerical simulations.
The numerical solution of singular eigenvalue problems is complicated by the fact that small perturbations of the coefficients may have an arbitrarily bad effect on eigenvalue accuracy. However, it has been known for a long time that such perturbations are exceptional and standard eigenvalue solvers, such as the QZ algorithm, tend to yield good accuracy despite the inevitable presence of roundoff error. Recently, Lotz and Noferini quantified this phenomenon by introducing the concept of $\delta$-weak eigenvalue condition numbers. In this work, we consider singular quadratic eigenvalue problems and two popular linearizations. Our results show that a correctly chosen linearization increases $\delta$-weak eigenvalue condition numbers only marginally, justifying the use of these linearizations in numerical solvers also in the singular case. We propose a very simple but often effective algorithm for computing well-conditioned eigenvalues of a singular quadratic eigenvalue problems by adding small random perturbations to the coefficients. We prove that the eigenvalue condition number is, with high probability, a reliable criterion for detecting and excluding spurious eigenvalues created from the singular part.
Object detection and tracking in videos represent essential and computationally demanding building blocks for current and future visual perception systems. In order to reduce the efficiency gap between available methods and computational requirements of real-world applications, we propose to re-think one of the most successful methods for image object detection, Faster R-CNN, and extend it to the video domain. Specifically, we extend the detection framework to learn instance-level embeddings which prove beneficial for data association and re-identification purposes. Focusing on the computational aspects of detection and tracking, our proposed method reaches a very high computational efficiency necessary for relevant applications, while still managing to compete with recent and state-of-the-art methods as shown in the experiments we conduct on standard object tracking benchmarks
In this paper we propose a novel sparse optical flow (SOF)-based line feature tracking method for the camera pose estimation problem. This method is inspired by the point-based SOF algorithm and developed based on an observation that two adjacent images in time-varying image sequences satisfy brightness invariant. Based on this observation, we re-define the goal of line feature tracking: track two endpoints of a line feature instead of the entire line based on gray value matching instead of descriptor matching. To achieve this goal, an efficient two endpoint tracking (TET) method is presented: first, describe a given line feature with its two endpoints; next, track the two endpoints based on SOF to obtain two new tracked endpoints by minimizing a pixel-level grayscale residual function; finally, connect the two tracked endpoints to generate a new line feature. The correspondence is established between the given and the new line feature. Compared with current descriptor-based methods, our TET method needs not to compute descriptors and detect line features repeatedly. Naturally, it has an obvious advantage over computation. Experiments in several public benchmark datasets show our method yields highly competitive accuracy with an obvious advantage over speed.
Since hardware resources are limited, the objective of training deep learning models is typically to maximize accuracy subject to the time and memory constraints of training and inference. We study the impact of model size in this setting, focusing on Transformer models for NLP tasks that are limited by compute: self-supervised pretraining and high-resource machine translation. We first show that even though smaller Transformer models execute faster per iteration, wider and deeper models converge in significantly fewer steps. Moreover, this acceleration in convergence typically outpaces the additional computational overhead of using larger models. Therefore, the most compute-efficient training strategy is to counterintuitively train extremely large models but stop after a small number of iterations. This leads to an apparent trade-off between the training efficiency of large Transformer models and the inference efficiency of small Transformer models. However, we show that large models are more robust to compression techniques such as quantization and pruning than small models. Consequently, one can get the best of both worlds: heavily compressed, large models achieve higher accuracy than lightly compressed, small models.