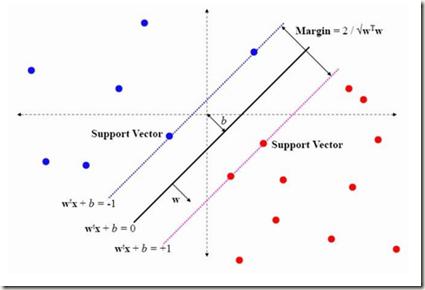
Recent advance on linear support vector machine with the 0-1 soft margin loss ($L_{0/1}$-SVM) shows that the 0-1 loss problem can be solved directly. However, its theoretical and algorithmic requirements restrict us extending the linear solving framework to its nonlinear kernel form directly, the absence of explicit expression of Lagrangian dual function of $L_{0/1}$-SVM is one big deficiency among of them. In this paper, by applying the nonparametric representation theorem, we propose a nonlinear model for support vector machine with 0-1 soft margin loss, called $L_{0/1}$-KSVM, which cunningly involves the kernel technique into it and more importantly, follows the success on systematically solving its linear task. Its optimal condition is explored theoretically and a working set selection alternating direction method of multipliers (ADMM) algorithm is introduced to acquire its numerical solution. Moreover, we firstly present a closed-form definition to the support vector (SV) of $L_{0/1}$-KSVM. Theoretically, we prove that all SVs of $L_{0/1}$-KSVM are only located on the parallel decision surfaces. The experiment part also shows that $L_{0/1}$-KSVM has much fewer SVs, simultaneously with a decent predicting accuracy, when comparing to its linear peer $L_{0/1}$-SVM and the other six nonlinear benchmark SVM classifiers.
相關內容
In many industrial applications, obtaining labeled observations is not straightforward as it often requires the intervention of human experts or the use of expensive testing equipment. In these circumstances, active learning can be highly beneficial in suggesting the most informative data points to be used when fitting a model. Reducing the number of observations needed for model development alleviates both the computational burden required for training and the operational expenses related to labeling. Online active learning, in particular, is useful in high-volume production processes where the decision about the acquisition of the label for a data point needs to be taken within an extremely short time frame. However, despite the recent efforts to develop online active learning strategies, the behavior of these methods in the presence of outliers has not been thoroughly examined. In this work, we investigate the performance of online active linear regression in contaminated data streams. Our study shows that the currently available query strategies are prone to sample outliers, whose inclusion in the training set eventually degrades the predictive performance of the models. To address this issue, we propose a solution that bounds the search area of a conditional D-optimal algorithm and uses a robust estimator. Our approach strikes a balance between exploring unseen regions of the input space and protecting against outliers. Through numerical simulations, we show that the proposed method is effective in improving the performance of online active learning in the presence of outliers, thus expanding the potential applications of this powerful tool.
In consumer theory, ranking available objects by means of preference relations yields the most common description of individual choices. However, preference-based models assume that individuals: (1) give their preferences only between pairs of objects; (2) are always able to pick the best preferred object. In many situations, they may be instead choosing out of a set with more than two elements and, because of lack of information and/or incomparability (objects with contradictory characteristics), they may not able to select a single most preferred object. To address these situations, we need a choice-model which allows an individual to express a set-valued choice. Choice functions provide such a mathematical framework. We propose a Gaussian Process model to learn choice functions from choice-data. The proposed model assumes a multiple utility representation of a choice function based on the concept of Pareto rationalization, and derives a strategy to learn both the number and the values of these latent multiple utilities. Simulation experiments demonstrate that the proposed model outperforms the state-of-the-art methods.
Anderson acceleration (AA) is a well-known method for accelerating the convergence of iterative algorithms, with applications in various fields including deep learning and optimization. Despite its popularity in these areas, the effectiveness of AA in classical machine learning classifiers has not been thoroughly studied. Tabular data, in particular, presents a unique challenge for deep learning models, and classical machine learning models are known to perform better in these scenarios. However, the convergence analysis of these models has received limited attention. To address this gap in research, we implement a support vector machine (SVM) classifier variant that incorporates AA to speed up convergence. We evaluate the performance of our SVM with and without Anderson acceleration on several datasets from the biology domain and demonstrate that the use of AA significantly improves convergence and reduces the training loss as the number of iterations increases. Our findings provide a promising perspective on the potential of Anderson acceleration in the training of simple machine learning classifiers and underscore the importance of further research in this area. By showing the effectiveness of AA in this setting, we aim to inspire more studies that explore the applications of AA in classical machine learning.
In this paper, we consider a bandit problem in which there are a number of groups each consisting of infinitely many arms. Whenever a new arm is requested from a given group, its mean reward is drawn from an unknown reservoir distribution (different for each group), and the uncertainty in the arm's mean reward can only be reduced via subsequent pulls of the arm. The goal is to identify the infinite-arm group whose reservoir distribution has the highest $(1-\alpha)$-quantile (e.g., median if $\alpha = \frac{1}{2}$), using as few total arm pulls as possible. We introduce a two-step algorithm that first requests a fixed number of arms from each group and then runs a finite-arm grouped max-quantile bandit algorithm. We characterize both the instance-dependent and worst-case regret, and provide a matching lower bound for the latter, while discussing various strengths, weaknesses, algorithmic improvements, and potential lower bounds associated with our instance-dependent upper bounds.
Stochastic gradient descent plays a fundamental role in nearly all applications of deep learning. However its ability to converge to a global minimum remains shrouded in mystery. In this paper we propose to study the behavior of the loss function on fixed mini-batches along SGD trajectories. We show that the loss function on a fixed batch appears to be remarkably convex-like. In particular for ResNet the loss for any fixed mini-batch can be accurately modeled by a quadratic function and a very low loss value can be reached in just one step of gradient descent with sufficiently large learning rate. We propose a simple model that allows to analyze the relationship between the gradients of stochastic mini-batches and the full batch. Our analysis allows us to discover the equivalency between iterate aggregates and specific learning rate schedules. In particular, for Exponential Moving Average (EMA) and Stochastic Weight Averaging we show that our proposed model matches the observed training trajectories on ImageNet. Our theoretical model predicts that an even simpler averaging technique, averaging just two points a many steps apart, significantly improves accuracy compared to the baseline. We validated our findings on ImageNet and other datasets using ResNet architecture.
The Boolean Satisfiability (SAT) problem stands out as an attractive NP-complete problem in theoretic computer science and plays a central role in a broad spectrum of computing-related applications. Exploiting and tuning SAT solvers under numerous scenarios require massive high-quality industry-level SAT instances, which unfortunately are quite limited in the real world. To address the data insufficiency issue, in this paper, we propose W2SAT, a framework to generate SAT formulas by learning intrinsic structures and properties from given real-world/industrial instances in an implicit fashion. To this end, we introduce a novel SAT representation called Weighted Literal Incidence Graph (WLIG), which exhibits strong representation ability and generalizability against existing counterparts, and can be efficiently generated via a specialized learning-based graph generative model. Decoding from WLIGs into SAT problems is then modeled as finding overlapping cliques with a novel hill-climbing optimization method termed Optimal Weight Coverage (OWC). Experiments demonstrate the superiority of our WLIG-induced approach in terms of graph metrics, efficiency, and scalability in comparison to previous methods. Additionally, we discuss the limitations of graph-based SAT generation for real-world applications, especially when utilizing generated instances for SAT solver parameter-tuning, and pose some potential directions.
Most state-of-the-art machine learning techniques revolve around the optimisation of loss functions. Defining appropriate loss functions is therefore critical to successfully solving problems in this field. We present a survey of the most commonly used loss functions for a wide range of different applications, divided into classification, regression, ranking, sample generation and energy based modelling. Overall, we introduce 33 different loss functions and we organise them into an intuitive taxonomy. Each loss function is given a theoretical backing and we describe where it is best used. This survey aims to provide a reference of the most essential loss functions for both beginner and advanced machine learning practitioners.
Standard contrastive learning approaches usually require a large number of negatives for effective unsupervised learning and often exhibit slow convergence. We suspect this behavior is due to the suboptimal selection of negatives used for offering contrast to the positives. We counter this difficulty by taking inspiration from support vector machines (SVMs) to present max-margin contrastive learning (MMCL). Our approach selects negatives as the sparse support vectors obtained via a quadratic optimization problem, and contrastiveness is enforced by maximizing the decision margin. As SVM optimization can be computationally demanding, especially in an end-to-end setting, we present simplifications that alleviate the computational burden. We validate our approach on standard vision benchmark datasets, demonstrating better performance in unsupervised representation learning over state-of-the-art, while having better empirical convergence properties.
In structure learning, the output is generally a structure that is used as supervision information to achieve good performance. Considering the interpretation of deep learning models has raised extended attention these years, it will be beneficial if we can learn an interpretable structure from deep learning models. In this paper, we focus on Recurrent Neural Networks (RNNs) whose inner mechanism is still not clearly understood. We find that Finite State Automaton (FSA) that processes sequential data has more interpretable inner mechanism and can be learned from RNNs as the interpretable structure. We propose two methods to learn FSA from RNN based on two different clustering methods. We first give the graphical illustration of FSA for human beings to follow, which shows the interpretability. From the FSA's point of view, we then analyze how the performance of RNNs are affected by the number of gates, as well as the semantic meaning behind the transition of numerical hidden states. Our results suggest that RNNs with simple gated structure such as Minimal Gated Unit (MGU) is more desirable and the transitions in FSA leading to specific classification result are associated with corresponding words which are understandable by human beings.
The key issue of few-shot learning is learning to generalize. In this paper, we propose a large margin principle to improve the generalization capacity of metric based methods for few-shot learning. To realize it, we develop a unified framework to learn a more discriminative metric space by augmenting the softmax classification loss function with a large margin distance loss function for training. Extensive experiments on two state-of-the-art few-shot learning models, graph neural networks and prototypical networks, show that our method can improve the performance of existing models substantially with very little computational overhead, demonstrating the effectiveness of the large margin principle and the potential of our method.