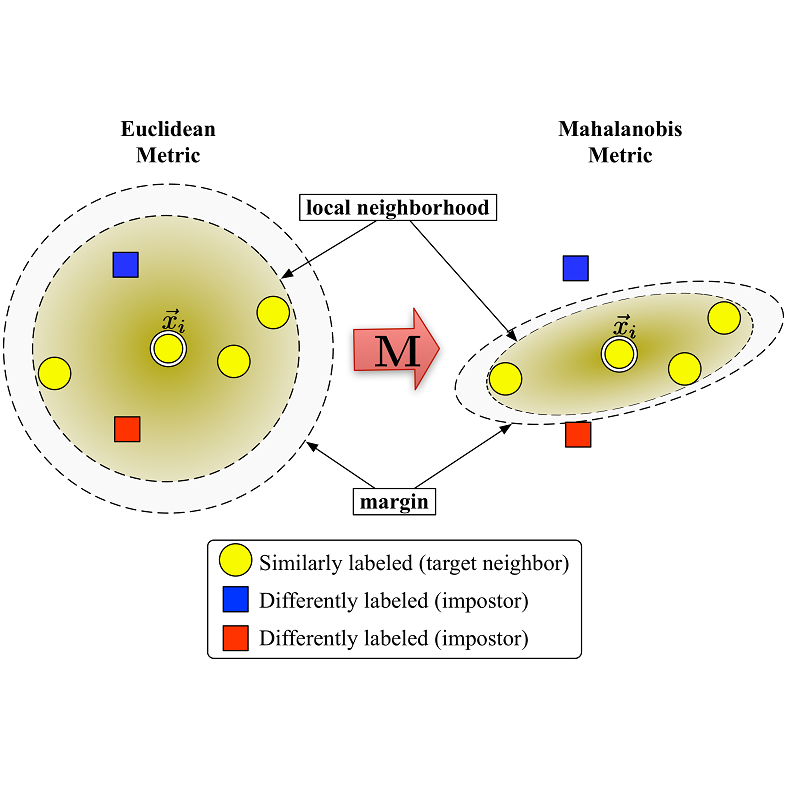
Deep metric learning (DML) aims to minimize empirical expected loss of the pairwise intra-/inter- class proximity violations in the embedding image. We relate DML to feasibility problem of finite chance constraints. We show that minimizer of proxy-based DML satisfies certain chance constraints, and that the worst case generalization performance of the proxy-based methods can be characterized by the radius of the smallest ball around a class proxy to cover the entire domain of the corresponding class samples, suggesting multiple proxies per class helps performance. To provide a scalable algorithm as well as exploiting more proxies, we consider the chance constraints implied by the minimizers of proxy-based DML instances and reformulate DML as finding a feasible point in intersection of such constraints, resulting in a problem to be approximately solved by iterative projections. Simply put, we repeatedly train a regularized proxy-based loss and re-initialize the proxies with the embeddings of the deliberately selected new samples. We apply our method with the well-accepted losses and evaluate on four popular benchmark datasets for image retrieval. Outperforming state-of-the-art, our method consistently improves the performance of the applied losses. Code is available at: //github.com/yetigurbuz/ccp-dml
相關內容
Variational autoencoders (VAEs) are a popular framework for modeling complex data distributions; they can be efficiently trained via variational inference by maximizing the evidence lower bound (ELBO), at the expense of a gap to the exact (log-)marginal likelihood. While VAEs are commonly used for representation learning, it is unclear why ELBO maximization would yield useful representations, since unregularized maximum likelihood estimation cannot invert the data-generating process. Yet, VAEs often succeed at this task. We seek to elucidate this apparent paradox by studying nonlinear VAEs in the limit of near-deterministic decoders. We first prove that, in this regime, the optimal encoder approximately inverts the decoder -- a commonly used but unproven conjecture -- which we refer to as {\em self-consistency}. Leveraging self-consistency, we show that the ELBO converges to a regularized log-likelihood. This allows VAEs to perform what has recently been termed independent mechanism analysis (IMA): it adds an inductive bias towards decoders with column-orthogonal Jacobians, which helps recovering the true latent factors. The gap between ELBO and log-likelihood is therefore welcome, since it bears unanticipated benefits for nonlinear representation learning. In experiments on synthetic and image data, we show that VAEs uncover the true latent factors when the data generating process satisfies the IMA assumption.
Enabling low precision implementations of deep learning models, without considerable performance degradation, is necessary in resource and latency constrained settings. Moreover, exploiting the differences in sensitivity to quantization across layers can allow mixed precision implementations to achieve a considerably better computation performance trade-off. However, backpropagating through the quantization operation requires introducing gradient approximations, and choosing which layers to quantize is challenging for modern architectures due to the large search space. In this work, we present a constrained learning approach to quantization aware training. We formulate low precision supervised learning as a constrained optimization problem, and show that despite its non-convexity, the resulting problem is strongly dual and does away with gradient estimations. Furthermore, we show that dual variables indicate the sensitivity of the objective with respect to constraint perturbations. We demonstrate that the proposed approach exhibits competitive performance in image classification tasks, and leverage the sensitivity result to apply layer selective quantization based on the value of dual variables, leading to considerable performance improvements.
Deep learning has achieved tremendous success by training increasingly large models, which are then compressed for practical deployment. We propose a drastically different approach to compact and optimal deep learning: We decouple the Degrees of freedom (DoF) and the actual number of parameters of a model, optimize a small DoF with predefined random linear constraints for a large model of arbitrary architecture, in one-stage end-to-end learning. Specifically, we create a recurrent parameter generator (RPG), which repeatedly fetches parameters from a ring and unpacks them onto a large model with random permutation and sign flipping to promote parameter decorrelation. We show that gradient descent can automatically find the best model under constraints with faster convergence. Our extensive experimentation reveals a log-linear relationship between model DoF and accuracy. Our RPG demonstrates remarkable DoF reduction and can be further pruned and quantized for additional run-time performance gain. For example, in terms of top-1 accuracy on ImageNet, RPG achieves $96\%$ of ResNet18's performance with only $18\%$ DoF (the equivalent of one convolutional layer) and $52\%$ of ResNet34's performance with only $0.25\%$ DoF! Our work shows a significant potential of constrained neural optimization in compact and optimal deep learning.
Comparing the functional behavior of neural network models, whether it is a single network over time or two (or more networks) during or post-training, is an essential step in understanding what they are learning (and what they are not), and for identifying strategies for regularization or efficiency improvements. Despite recent progress, e.g., comparing vision transformers to CNNs, systematic comparison of function, especially across different networks, remains difficult and is often carried out layer by layer. Approaches such as canonical correlation analysis (CCA) are applicable in principle, but have been sparingly used so far. In this paper, we revisit a (less widely known) from statistics, called distance correlation (and its partial variant), designed to evaluate correlation between feature spaces of different dimensions. We describe the steps necessary to carry out its deployment for large scale models -- this opens the door to a surprising array of applications ranging from conditioning one deep model w.r.t. another, learning disentangled representations as well as optimizing diverse models that would directly be more robust to adversarial attacks. Our experiments suggest a versatile regularizer (or constraint) with many advantages, which avoids some of the common difficulties one faces in such analyses. Code is at //github.com/zhenxingjian/Partial_Distance_Correlation.
Many recent loss functions in deep metric learning are expressed with logarithmic and exponential forms, and they involve margin and scale as essential hyper-parameters. Since each data class has an intrinsic characteristic, several previous works have tried to learn embedding space close to the real distribution by introducing adaptive margins. However, there was no work on adaptive scales at all. We argue that both margin and scale should be adaptively adjustable during the training. In this paper, we propose a method called Adaptive Margin and Scale (AdaMS), where hyper-parameters of margin and scale are replaced with learnable parameters of adaptive margins and adaptive scales for each class. Our method is evaluated on Wall Street Journal dataset, and we achieve outperforming results for word discrimination tasks.
In this paper, we tackle a novel federated learning (FL) problem for optimizing a family of compositional pairwise risks, to which no existing FL algorithms are applicable. In particular, the objective has the form of $\mathbb E_{\mathbf z\sim \mathcal S_1} f(\mathbb E_{\mathbf z'\sim\mathcal S_2} \ell(\mathbf w, \mathbf z, \mathbf z'))$, where two sets of data $\mathcal S_1, \mathcal S_2$ are distributed over multiple machines, $\ell(\cdot; \cdot,\cdot)$ is a pairwise loss that only depends on the prediction outputs of the input data pairs $(\mathbf z, \mathbf z')$, and $f(\cdot)$ is possibly a non-linear non-convex function. This problem has important applications in machine learning, e.g., AUROC maximization with a pairwise loss, and partial AUROC maximization with a compositional loss. The challenges for designing an FL algorithm lie in the non-decomposability of the objective over multiple machines and the interdependency between different machines. We propose two provable FL algorithms (FedX) for handling linear and nonlinear $f$, respectively. To address the challenges, we decouple the gradient's components with two types, namely active parts and lazy parts, where the active parts depend on local data that are computed with the local model and the lazy parts depend on other machines that are communicated/computed based on historical models and samples. We develop a novel theoretical analysis to combat the latency of the lazy parts and the interdependency between the local model parameters and the involved data for computing local gradient estimators. We establish both iteration and communication complexities and show that using the historical samples and models for computing the lazy parts do not degrade the complexities. We conduct empirical studies of FedX for deep AUROC and partial AUROC maximization, and demonstrate their performance compared with several baselines.
The interplay between Machine Learning (ML) and Constrained Optimization (CO) has recently been the subject of increasing interest, leading to a new and prolific research area covering (e.g.) Decision Focused Learning and Constrained Reinforcement Learning. Such approaches strive to tackle complex decision problems under uncertainty over multiple stages, involving both explicit (cost function, constraints) and implicit knowledge (from data), and possibly subject to execution time restrictions. While a good degree of success has been achieved, the existing methods still have limitations in terms of both applicability and effectiveness. For problems in this class, we propose UNIFY, a unified framework to design a solution policy for complex decision-making problems. Our approach relies on a clever decomposition of the policy in two stages, namely an unconstrained ML model and a CO problem, to take advantage of the strength of each approach while compensating for its weaknesses. With a little design effort, UNIFY can generalize several existing approaches, thus extending their applicability. We demonstrate the method effectiveness on two practical problems, namely an Energy Management System and the Set Multi-cover with stochastic coverage requirements. Finally, we highlight some current challenges of our method and future research directions that can benefit from the cross-fertilization of the two fields.
For deploying a deep learning model into production, it needs to be both accurate and compact to meet the latency and memory constraints. This usually results in a network that is deep (to ensure performance) and yet thin (to improve computational efficiency). In this paper, we propose an efficient method to train a deep thin network with a theoretic guarantee. Our method is motivated by model compression. It consists of three stages. In the first stage, we sufficiently widen the deep thin network and train it until convergence. In the second stage, we use this well-trained deep wide network to warm up (or initialize) the original deep thin network. This is achieved by letting the thin network imitate the immediate outputs of the wide network from layer to layer. In the last stage, we further fine tune this well initialized deep thin network. The theoretical guarantee is established by using mean field analysis, which shows the advantage of layerwise imitation over traditional training deep thin networks from scratch by backpropagation. We also conduct large-scale empirical experiments to validate our approach. By training with our method, ResNet50 can outperform ResNet101, and BERT_BASE can be comparable with BERT_LARGE, where both the latter models are trained via the standard training procedures as in the literature.
Recently, ensemble has been applied to deep metric learning to yield state-of-the-art results. Deep metric learning aims to learn deep neural networks for feature embeddings, distances of which satisfy given constraint. In deep metric learning, ensemble takes average of distances learned by multiple learners. As one important aspect of ensemble, the learners should be diverse in their feature embeddings. To this end, we propose an attention-based ensemble, which uses multiple attention masks, so that each learner can attend to different parts of the object. We also propose a divergence loss, which encourages diversity among the learners. The proposed method is applied to the standard benchmarks of deep metric learning and experimental results show that it outperforms the state-of-the-art methods by a significant margin on image retrieval tasks.
Learning similarity functions between image pairs with deep neural networks yields highly correlated activations of embeddings. In this work, we show how to improve the robustness of such embeddings by exploiting the independence within ensembles. To this end, we divide the last embedding layer of a deep network into an embedding ensemble and formulate training this ensemble as an online gradient boosting problem. Each learner receives a reweighted training sample from the previous learners. Further, we propose two loss functions which increase the diversity in our ensemble. These loss functions can be applied either for weight initialization or during training. Together, our contributions leverage large embedding sizes more effectively by significantly reducing correlation of the embedding and consequently increase retrieval accuracy of the embedding. Our method works with any differentiable loss function and does not introduce any additional parameters during test time. We evaluate our metric learning method on image retrieval tasks and show that it improves over state-of-the-art methods on the CUB 200-2011, Cars-196, Stanford Online Products, In-Shop Clothes Retrieval and VehicleID datasets.