Given an image $u_0$, the aim of minimising the Mumford-Shah functional is to find a decomposition of the image domain into sub-domains and a piecewise smooth approximation $u$ of $u_0$ such that $u$ varies smoothly within each sub-domain. Since the Mumford-Shah functional is highly non-smooth, regularizations such as the Ambrosio-Tortorelli approximation can be considered which is one of the most computationally efficient approximations of the Mumford-Shah functional for image segmentation. Our main result is the $\Gamma$-convergence of the Ambrosio-Tortorelli approximation of the Mumford-Shah functional for piecewise smooth approximations. This requires the introduction of an appropriate function space. As a consequence of our $\Gamma$-convergence result, we can infer the convergence of minimizers of the respective functionals.
相關內容
We consider the Cauchy problem for the Helmholtz equation with a domain in R^d, d>2 with N cylindrical outlets to infinity with bounded inclusions in R^{d-1}. Cauchy data are prescribed on the boundary of the bounded domains and the aim is to find solution on the unbounded part of the boundary. In 1989, Kozlov and Maz'ya proposed an alternating iterative method for solving Cauchy problems associated with elliptic,self-adjoint and positive-definite operators in bounded domains. Different variants of this method for solving Cauchy problems associated with Helmholtz-type operators exists. We consider the variant proposed by Mpinganzima et al. for bounded domains and derive the necessary conditions for the convergence of the procedure in unbounded domains. For the numerical implementation, a finite difference method is used to solve the problem in a simple rectangular domain in R^2 that represent a truncated infinite strip. The numerical results shows that by appropriate truncation of the domain and with appropriate choice of the Robin parameters, the Robin-Dirichlet alternating iterative procedure is convergent.
The basic goal of survivable network design is to build cheap networks that guarantee the connectivity of certain pairs of nodes despite the failure of a few edges or nodes. A celebrated result by Jain [Combinatorica'01] provides a 2-approximation for a wide class of these problems. However nothing better is known even for very basic special cases, raising the natural question whether any improved approximation factor is possible at all. In this paper we address one of the most basic problems in this family for which 2 is still the best-known approximation factor, the Forest Augmentation Problem (FAP): given an undirected unweighted graph (that w.l.o.g. is a forest) and a collection of extra edges (links), compute a minimum cardinality subset of links whose addition to the graph makes it 2-edge-connected. Several better-than-2 approximation algorithms are known for the special case where the input graph is a tree, a.k.a. the Tree Augmentation Problem (TAP). Recently this was achieved also for the weighted version of TAP, and for the k-edge-connectivity generalization of TAP. These results heavily exploit the fact that the input graph is connected, a condition that does not hold in FAP. In this paper we breach the 2-approximation barrier for FAP. Our result is based on two main ingredients. First, we describe a reduction to the Path Augmentation Problem (PAP), the special case of FAP where the input graph is a collection of disjoint paths. Our reduction is not approximation preserving, however it is sufficiently accurate to improve on a factor 2 approximation. Second, we present a better-than-2 approximation algorithm for PAP, an open problem on its own. Here we exploit a novel notion of implicit credits which might turn out to be helpful in future related work.
This paper investigates a new downlink nonorthogonal multiple access (NOMA) system, where a multiantenna unmanned aerial vehicle (UAV) is powered by wireless power transfer (WPT) and serves as the base station for multiple pairs of ground users (GUs) running NOMA in each pair. An energy efficiency (EE) maximization problem is formulated to jointly optimize the WPT time and the placement for the UAV, and the allocation of the UAV's transmit power between different NOMA user pairs and within each pair. To efficiently solve this nonconvex problem, we decompose the problem into three subproblems using block coordinate descent. For the subproblem of intra-pair power allocation within each NOMA user pair, we construct a supermodular game with confirmed convergence to a Nash equilibrium. Given the intra-pair power allocation, successive convex approximation is applied to convexify and solve the subproblem of WPT time allocation and inter-pair power allocation between the user pairs. Finally, we solve the subproblem of UAV placement by using the Lagrange multiplier method. Simulations show that our approach can substantially outperform its alternatives that do not use NOMA and WPT techniques or that do not optimize the UAV location.
The Schrijver graph $S(n,k)$ is defined for integers $n$ and $k$ with $n \geq 2k$ as the graph whose vertices are all the $k$-subsets of $\{1,2,\ldots,n\}$ that do not include two consecutive elements modulo $n$, where two such sets are adjacent if they are disjoint. A result of Schrijver asserts that the chromatic number of $S(n,k)$ is $n-2k+2$ (Nieuw Arch. Wiskd., 1978). In the computational Schrijver problem, we are given an access to a coloring of the vertices of $S(n,k)$ with $n-2k+1$ colors, and the goal is to find a monochromatic edge. The Schrijver problem is known to be complete in the complexity class $\mathsf{PPA}$. We prove that it can be solved by a randomized algorithm with running time $n^{O(1)} \cdot k^{O(k)}$, hence it is fixed-parameter tractable with respect to the parameter $k$.
Given a set $P$ of $n$ points in the plane, the $k$-center problem is to find $k$ congruent disks of minimum possible radius such that their union covers all the points in $P$. The $2$-center problem is a special case of the $k$-center problem that has been extensively studied in the recent past \cite{CAHN,HT,SH}. In this paper, we consider a generalized version of the $2$-center problem called \textit{proximity connected} $2$-center (PCTC) problem. In this problem, we are also given a parameter $\delta\geq 0$ and we have the additional constraint that the distance between the centers of the disks should be at most $\delta$. Note that when $\delta=0$, the PCTC problem is reduced to the $1$-center(minimum enclosing disk) problem and when $\delta$ tends to infinity, it is reduced to the $2$-center problem. The PCTC problem first appeared in the context of wireless networks in 1992 \cite{ACN0}, but obtaining a nontrivial deterministic algorithm for the problem remained open. In this paper, we resolve this open problem by providing a deterministic $O(n^2\log n)$ time algorithm for the problem.
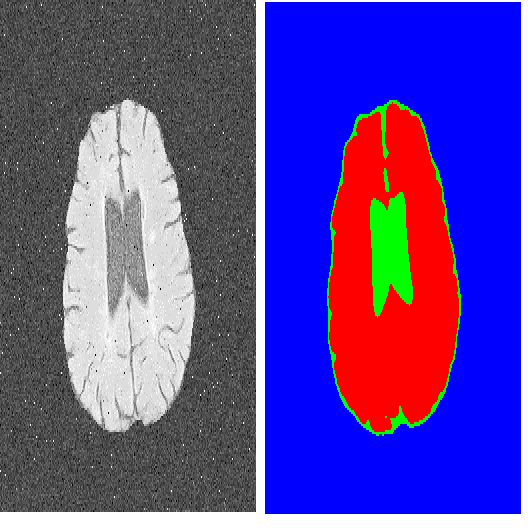
The geometric high-order regularization methods such as mean curvature and Gaussian curvature, have been intensively studied during the last decades due to their abilities in preserving geometric properties including image edges, corners, and image contrast. However, the dilemma between restoration quality and computational efficiency is an essential roadblock for high-order methods. In this paper, we propose fast multi-grid algorithms for minimizing both mean curvature and Gaussian curvature energy functionals without sacrificing the accuracy for efficiency. Unlike the existing approaches based on operator splitting and the Augmented Lagrangian method (ALM), no artificial parameters are introduced in our formulation, which guarantees the robustness of the proposed algorithm. Meanwhile, we adopt the domain decomposition method to promote parallel computing and use the fine-to-coarse structure to accelerate the convergence. Numerical experiments are presented on both image denoising and CT reconstruction problem to demonstrate the ability to recover image texture and the efficiency of the proposed method.
In the storied Colonel Blotto game, two colonels allocate $a$ and $b$ troops, respectively, to $k$ distinct battlefields. A colonel wins a battle if they assign more troops to that particular battle, and each colonel seeks to maximize their total number of victories. Despite the problem's formulation in 1921, the first polynomial-time algorithm to compute Nash equilibrium (NE) strategies for this game was discovered only quite recently. In 2016, \citep{ahmadinejad_dehghani_hajiaghayi_lucier_mahini_seddighin_2019} formulated a breakthrough algorithm to compute NE strategies for the Colonel Blotto game\footnote{To the best of our knowledge, the algorithm from \citep{ahmadinejad_dehghani_hajiaghayi_lucier_mahini_seddighin_2019} has computational complexity $O(k^{14}\max\{a,b\}^{13})$}, receiving substantial media coverage (e.g. \citep{Insider}, \citep{NSF}, \citep{ScienceDaily}). In this work, we present the first known $\epsilon$-approximation algorithm to compute NE strategies in the two-player Colonel Blotto game in runtime $\widetilde{O}(\epsilon^{-4} k^8 \max\{a,b\}^2)$ for arbitrary settings of these parameters. Moreover, this algorithm computes approximate coarse correlated equilibrium strategies in the multiplayer (continuous and discrete) Colonel Blotto game (when there are $\ell > 2$ colonels) with runtime $\widetilde{O}(\ell \epsilon^{-4} k^8 n^2 + \ell^2 \epsilon^{-2} k^3 n (n+k))$, where $n$ is the maximum troop count. Before this work, no polynomial-time algorithm was known to compute exact or approximate equilibrium (in any sense) strategies for multiplayer Colonel Blotto with arbitrary parameters. Our algorithm computes these approximate equilibria by a novel (to the author's knowledge) sampling technique with which we implicitly perform multiplicative weights update over the exponentially many strategies available to each player.
We consider smooth optimization problems with a Hermitian positive semi-definite fixed-rank constraint, where a quotient geometry with three Riemannian metrics $g^i(\cdot, \cdot)$ $(i=1,2,3)$ is used to represent this constraint. By taking the nonlinear conjugate gradient method (CG) as an example, we show that CG on the quotient geometry with metric $g^1$ is equivalent to CG on the factor-based optimization framework, which is often called the Burer--Monteiro approach. We also show that CG on the quotient geometry with metric $g^3$ is equivalent to CG on the commonly-used embedded geometry. We call two CG methods equivalent if they produce an identical sequence of iterates $\{X_k\}$. In addition, we show that if the limit point of the sequence $\{X_k\}$ generated by an algorithm has lower rank, that is $X_k\in \mathbb C^{n\times n}, k = 1, 2, \ldots$ has rank $p$ and the limit point $X_*$ has rank $r < p$, then the condition number of the Riemannian Hessian with metric $g^1$ can be unbounded, but those of the other two metrics stay bounded. Numerical experiments show that the Burer--Monteiro CG method has slower local convergence rate if the limit point has a reduced rank, compared to CG on the quotient geometry under the other two metrics. This slower convergence rate can thus be attributed to the large condition number of the Hessian near a minimizer.
The stochastic gradient Langevin Dynamics is one of the most fundamental algorithms to solve sampling problems and non-convex optimization appearing in several machine learning applications. Especially, its variance reduced versions have nowadays gained particular attention. In this paper, we study two variants of this kind, namely, the Stochastic Variance Reduced Gradient Langevin Dynamics and the Stochastic Recursive Gradient Langevin Dynamics. We prove their convergence to the objective distribution in terms of KL-divergence under the sole assumptions of smoothness and Log-Sobolev inequality which are weaker conditions than those used in prior works for these algorithms. With the batch size and the inner loop length set to $\sqrt{n}$, the gradient complexity to achieve an $\epsilon$-precision is $\tilde{O}((n+dn^{1/2}\epsilon^{-1})\gamma^2 L^2\alpha^{-2})$, which is an improvement from any previous analyses. We also show some essential applications of our result to non-convex optimization.
The minimum energy path (MEP) describes the mechanism of reaction, and the energy barrier along the path can be used to calculate the reaction rate in thermal systems. The nudged elastic band (NEB) method is one of the most commonly used schemes to compute MEPs numerically. It approximates an MEP by a discrete set of configuration images, where the discretization size determines both computational cost and accuracy of the simulations. In this paper, we consider a discrete MEP to be a stationary state of the NEB method and prove an optimal convergence rate of the discrete MEP with respect to the number of images. Numerical simulations for the transitions of some several proto-typical model systems are performed to support the theory.