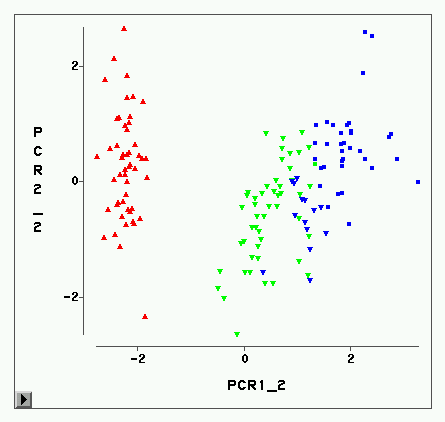
In this paper, we consider feature screening for ultrahigh dimensional clustering analyses. Based on the observation that the marginal distribution of any given feature is a mixture of its conditional distributions in different clusters, we propose to screen clustering features by independently evaluating the homogeneity of each feature's mixture distribution. Important cluster-relevant features have heterogeneous components in their mixture distributions and unimportant features have homogeneous components. The well-known EM-test statistic is used to evaluate the homogeneity. Under general parametric settings, we establish the tail probability bounds of the EM-test statistic for the homogeneous and heterogeneous features, and further show that the proposed screening procedure can achieve the sure independent screening and even the consistency in selection properties. Limiting distribution of the EM-test statistic is also obtained for general parametric distributions. The proposed method is computationally efficient, can accurately screen for important cluster-relevant features and help to significantly improve clustering, as demonstrated in our extensive simulation and real data analyses.
相關內容
Motivated by a heat radiative transport equation, we consider a particle undergoing collisions in a space-time domain and propose a method to sample its escape time, space and direction from the domain. The first step of the procedure is an estimation of how many elementary collisions is safe to take before chances of exiting the domain are too high; then these collisions are aggregated into a single movement. The method does not use any model nor any particular regime of parameters. We give theoretical results both under the normal approximation and without it and test the method on some benchmarks from the literature. The results confirm the theoretical predictions and show that the proposal is an efficient method to sample the escape distribution of the particle.
In recent years, power analysis has become widely used in applied sciences, with the increasing importance of the replicability issue. When distribution-free methods, such as Partial Least Squares (PLS)-based approaches, are considered, formulating power analysis turns out to be challenging. In this study, we introduce the methodological framework of a new procedure for performing power analysis when PLS-based methods are used. Data are simulated by the Monte Carlo method, assuming the null hypothesis of no effect is false and exploiting the latent structure estimated by PLS in the pilot data. In this way, the complex correlation data structure is explicitly considered in power analysis and sample size estimation. The paper offers insights into selecting statistical tests for the power analysis procedure, comparing accuracy-based tests and those based on continuous parameters estimated by PLS. Simulated and real datasets are investigated to show how the method works in practice.
In this thesis, we study problems at the interface of analysis and discrete mathematics. We discuss analogues of well known Hardy-type inequalities and Rearrangement inequalities on the lattice graphs $\mathbb{Z}^d$, with a particular focus on behaviour of sharp constants and optimizers.In the first half of the thesis, we analyse Hardy inequalities on $\mathbb{Z}^d$, first for $d=1$ and then for $d \geq 3$. We prove a sharp weighted Hardy inequality on integers with power weights of the form $n^\alpha$. This is done via two different methods, namely super-solution and Fourier method. We also use Fourier method to prove a weighted Hardy type inequality for higher order operators. After discussing the one dimensional case, we study the Hardy inequality in higher dimensions ($d \geq 3$). In particular, we compute the asymptotic behaviour of the sharp constant in the discrete Hardy inequality, as $d \rightarrow \infty$. This is done by converting the inequality into a continuous Hardy-type inequality on a torus for functions having zero average. These continuous inequalities are new and interesting in themselves. In the second half, we focus our attention on analogues of Rearrangement inequalities on lattice graphs. We begin by analysing the situation in dimension one. We define various notions of rearrangements and prove the corresponding Polya-Szeg\H{o} inequality. These inequalities are also applied to prove some weighted Hardy inequalities on integers. Finally, we study Rearrangement inequalities (Polya-Szeg\H{o}) on general graphs, with a particular focus on lattice graphs $\mathbb{Z}^d$, for $d \geq 2$. We develop a framework to study these inequalities, using which we derive concrete results in dimension two. In particular, these results develop connections between Polya-Szeg\H{o} inequality and various isoperimetric inequalities on graphs.
As language models (LMs) become more capable, it is increasingly important to align them with human preferences. However, the dominant paradigm for training Preference Models (PMs) for that purpose suffers from fundamental limitations, such as lack of transparency and scalability, along with susceptibility to overfitting the preference dataset. We propose Compositional Preference Models (CPMs), a novel PM framework that decomposes one global preference assessment into several interpretable features, obtains scalar scores for these features from a prompted LM, and aggregates these scores using a logistic regression classifier. Through these simple steps, CPMs allow to control which properties of the preference data are used to train the preference model and to build it based on features that are believed to underlie the human preference judgment. Our experiments show that CPMs not only improve generalization and are more robust to overoptimization than standard PMs, but also that best-of-n samples obtained using CPMs tend to be preferred over samples obtained using conventional PMs. Overall, our approach demonstrates the benefits of endowing PMs with priors about which features determine human preferences while relying on LM capabilities to extract those features in a scalable and robust way.
In this paper, we propose, analyze and demonstrate a dynamic momentum method to accelerate power and inverse power iterations with minimal computational overhead. The method is appropriate for real, diagonalizable matrices, and does not require a priori spectral knowledge. We review and extend background results on previously developed static momentum accelerations for the power iteration through the connection between the momentum accelerated iteration and the standard power iteration applied to an augmented matrix. We show that the augmented matrix is defective for the optimal parameter choice. We then present our dynamic method which updates the momentum parameter at each iteration based on the Rayleigh quotient and two previous residuals. We present convergence and stability theory for the method by considering a power-like method consisting of multiplying an initial vector by a sequence of augmented matrices. We demonstrate the developed method on a number of benchmark problems, and see that it outperforms both the power iteration and often the static momentum acceleration with optimal parameter choice. Finally, we present and demonstrate an explicit extension of the algorithm to inverse power iterations.
Making use of a newly developed package in the computer algebra system SageMath, we show how to perform a full asymptotic analysis by means of the Mellin transform with explicit error bounds. As an application of the method, we answer a question of B\'ona and DeJonge on 132-avoiding permutations with a unique longest increasing subsequence that can be translated into an inequality for a certain binomial sum.
In this paper, we present a~generalisation of proof simulation procedures for Frege systems by Bonet and Buss to some logics for which the deduction theorem does not hold. In particular, we study the case of finite-valued \L{}ukasiewicz logics. To this end, we provide proof systems that augment Avron's Frege system for \L{}ukasiewicz three-valued logic with nested and general versions of the disjunction elimination rule, respectively. For these systems we provide upper bounds on speed-ups w.r.t.\ both the number of steps in proofs and the length of proofs. We also consider Tamminga's natural deduction and Avron's hypersequent calculus for 3-valued \L{}ukasiewicz logic and generalise our results considering the disjunction elimination rule to all finite-valued \L{}ukasiewicz logics.
Distillation is the task of replacing a complicated machine learning model with a simpler model that approximates the original [BCNM06,HVD15]. Despite many practical applications, basic questions about the extent to which models can be distilled, and the runtime and amount of data needed to distill, remain largely open. To study these questions, we initiate a general theory of distillation, defining PAC-distillation in an analogous way to PAC-learning [Val84]. As applications of this theory: (1) we propose new algorithms to extract the knowledge stored in the trained weights of neural networks -- we show how to efficiently distill neural networks into succinct, explicit decision tree representations when possible by using the ``linear representation hypothesis''; and (2) we prove that distillation can be much cheaper than learning from scratch, and make progress on characterizing its complexity.
In this paper, we present and analyze fully discrete finite difference schemes designed for solving the initial value problem associated with the fractional Korteweg-de Vries (KdV) equation involving the fractional Laplacian. We design the scheme by introducing the discrete fractional Laplacian operator which is consistent with the continuous operator, and posses certain properties which are instrumental for the convergence analysis. Assuming the initial data (u_0 \in H^{1+\alpha}(\mathbb{R})), where (\alpha \in [1,2)), our study establishes the convergence of the approximate solutions obtained by the fully discrete finite difference schemes to a classical solution of the fractional KdV equation. Theoretical results are validated through several numerical illustrations for various values of fractional exponent $\alpha$. Furthermore, we demonstrate that the Crank-Nicolson finite difference scheme preserves the inherent conserved quantities along with the improved convergence rates.
Non-probability survey samples are examples of data sources that have become increasingly popular in recent years, also in official statistics. However, statistical inference based on non-probability samples is much more difficult because they are biased and are not representative of the target population (Wu, 2022). In this paper we consider a method of joint calibration for totals (Deville & S\"arndal, 1992) and quantiles (Harms & Duchesne, 2006) and use the proposed approach to extend existing inference methods for non-probability samples, such as inverse probability weighting, mass imputation and doubly robust estimators. By including quantile information in the estimation process non-linear relationships between the target and auxiliary variables can be approximated the way it is done in step-wise (constant) regression. Our simulation study has demonstrated that the estimators in question are more robust against model mis-specification and, as a result, help to reduce bias and improve estimation efficiency. Variance estimation for our proposed approach is also discussed. We show that existing inference methods can be used and that the resulting confidence intervals are at nominal levels. Finally, we applied the proposed methods to estimate the share of vacancies aimed at Ukrainian workers in Poland using an integrated set of administrative and survey data about job vacancies. The proposed approaches have been implemented in two R packages (nonprobsvy and jointCalib), which were used to conduct the simulation and empirical study