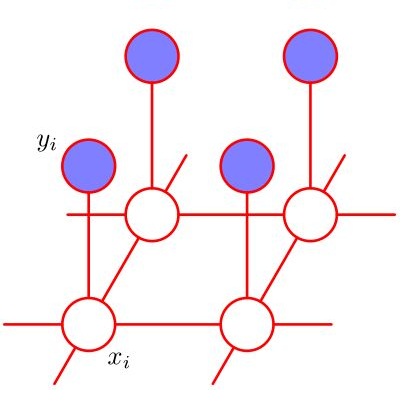
Claiming causal inferences in network settings necessitates careful consideration of the often complex dependency between outcomes for actors. Of particular importance are treatment spillover or outcome interference effects. We consider causal inference when the actors are connected via an underlying network structure. Our key contribution is a model for causality when the underlying network is unobserved and the actor covariates evolve stochastically over time. We develop a joint model for the relational and covariate generating process that avoids restrictive separability assumptions and deterministic network assumptions that do not hold in the majority of social network settings of interest. Our framework utilizes the highly general class of Exponential-family Random Network models (ERNM) of which Markov Random Fields (MRF) and Exponential-family Random Graph models (ERGM) are special cases. We present potential outcome based inference within a Bayesian framework, and propose a simple modification to the exchange algorithm to allow for sampling from ERNM posteriors. We present results of a simulation study demonstrating the validity of the approach. Finally, we demonstrate the value of the framework in a case-study of smoking over time in the context of adolescent friendship networks.
相關內容
We introduce two models of consensus following a majority rule on time-evolving stochastic block models (SBM), in which the network evolution is Markovian or non-Markovian. Under the majority rule, in each round, each agent simultaneously updates his/her opinion according to the majority of his/her neighbors. Our network has a community structure and randomly evolves with time. In contrast to the classic setting, the dynamics is not purely deterministic, and reflects the structure of SBM by resampling the connections at each step, making agents with the same opinion more likely to connect than those with different opinions. In the \emph{Markovian model}, connections between agents are resampled at each step according to the SBM law and each agent updates his/her opinion via the majority rule. We prove a \emph{power-of-one} type result, i.e., any initial bias leads to a non-trivial advantage of winning in the end, uniformly in the size of the network. In the \emph{non-Markovian model}, a connection between two agents is resampled according to the SBM law only when some of the two changes opinion and is otherwise kept the same. We study the phase transition between the fast convergence to the consensus and a halt of the dynamics. Moreover, we establish thresholds of the initial lead for various convergence speeds.
Active inference provides a general framework for behavior and learning in autonomous agents. It states that an agent will attempt to minimize its variational free energy, defined in terms of beliefs over observations, internal states and policies. Traditionally, every aspect of a discrete active inference model must be specified by hand, i.e. by manually defining the hidden state space structure, as well as the required distributions such as likelihood and transition probabilities. Recently, efforts have been made to learn state space representations automatically from observations using deep neural networks. In this paper, we present a novel approach of learning state spaces using quantum physics-inspired tensor networks. The ability of tensor networks to represent the probabilistic nature of quantum states as well as to reduce large state spaces makes tensor networks a natural candidate for active inference. We show how tensor networks can be used as a generative model for sequential data. Furthermore, we show how one can obtain beliefs from such a generative model and how an active inference agent can use these to compute the expected free energy. Finally, we demonstrate our method on the classic T-maze environment.
With an increased amount and availability of unmanned aerial vehicles (UAVs) and other remote sensing devices (e.g. satellites), we have recently seen a vast increase in computer vision methods for aerial view data. One application of such technologies is within search-and-rescue (SAR), where the task is to localize and assist one or several people who are missing, for example after a natural disaster. In many cases the rough location may be known and a UAV can be deployed to explore a given, confined area to precisely localize the missing people. Due to time and battery constraints it is often critical that localization is performed as efficiently as possible. In this work, we approach this type of problem by abstracting it as an aerial view goal localization task in a framework that emulates a SAR-like setup without requiring access to actual UAVs. In this framework, an agent operates on top of an aerial image (proxy for a search area) and is tasked with localizing a goal that is described in terms of visual cues. To further mimic the situation on an actual UAV, the agent is not able to observe the search area in its entirety, not even at low resolution, and thus it has to operate solely based on partial glimpses when navigating towards the goal. To tackle this task, we propose AiRLoc, a reinforcement learning (RL)-based model that decouples exploration (searching for distant goals) and exploitation (localizing nearby goals). Extensive evaluations show that AiRLoc outperforms heuristic search methods as well as alternative learnable approaches. We also conduct a proof-of-concept study which indicates that the learnable methods outperform humans on average. Code has been made publicly available: //github.com/aleksispi/airloc.
Inferring dependencies between complex biological traits while accounting for evolutionary relationships between specimens is of great scientific interest yet remains infeasible when trait and specimen counts grow large. The state-of-the-art approach uses a phylogenetic multivariate probit model to accommodate binary and continuous traits via a latent variable framework, and utilizes an efficient bouncy particle sampler (BPS) to tackle the computational bottleneck -- integrating many latent variables from a high-dimensional truncated normal distribution. This approach breaks down as the number of specimens grows and fails to reliably characterize conditional dependencies between traits. Here, we propose an inference pipeline for phylogenetic probit models that greatly outperforms BPS. The novelty lies in 1) a combination of the recent Zigzag Hamiltonian Monte Carlo (Zigzag-HMC) with linear-time gradient evaluations and 2) a joint sampling scheme for highly correlated latent variables and correlation matrix elements. In an application exploring HIV-1 evolution from 535 viruses, the inference requires joint sampling from an 11,235-dimensional truncated normal and a 24-dimensional covariance matrix. Our method yields a 5-fold speedup compared to BPS and makes it possible to learn partial correlations between candidate viral mutations and virulence. Computational speedup now enables us to tackle even larger problems: we study the evolution of influenza H1N1 glycosylations on around 900 viruses. For broader applicability, we extend the phylogenetic probit model to incorporate categorical traits, and demonstrate its use to study Aquilegia flower and pollinator co-evolution.
Reconstructing the causal relationships behind the phenomena we observe is a fundamental challenge in all areas of science. Discovering causal relationships through experiments is often infeasible, unethical, or expensive in complex systems. However, increases in computational power allow us to process the ever-growing amount of data that modern science generates, leading to an emerging interest in the causal discovery problem from observational data. This work evaluates the LPCMCI algorithm, which aims to find generators compatible with a multi-dimensional, highly autocorrelated time series while some variables are unobserved. We find that LPCMCI performs much better than a random algorithm mimicking not knowing anything but is still far from optimal detection. Furthermore, LPCMCI performs best on auto-dependencies, then contemporaneous dependencies, and struggles most with lagged dependencies. The source code of this project is available online.
In this work, we consider the spatial-temporal multi-species competition model. A mathematical model is described by a coupled system of nonlinear diffusion-reaction equations. We use a finite volume approximation with semi-implicit time approximation for the numerical solution of the model with corresponding boundary and initial conditions. To understand the effect of the diffusion to solution in one and two-dimensional formulations, we present numerical results for several cases of the parameters related to the survival scenarios. The random initial conditions' effect on the time to reach equilibrium is investigated. The influence of diffusion on the survival scenarios is presented. In real-world problems, values of the parameters are usually unknown and vary in some range. In order to evaluate the impact of parameters on the system stability, we simulate a spatial-temporal model with random parameters and perform factor analysis for two and three-species competition models.
In the context of solving inverse problems for physics applications within a Bayesian framework, we present a new approach, Markov Chain Generative Adversarial Neural Networks (MCGANs), to alleviate the computational costs associated with solving the Bayesian inference problem. GANs pose a very suitable framework to aid in the solution of Bayesian inference problems, as they are designed to generate samples from complicated high-dimensional distributions. By training a GAN to sample from a low-dimensional latent space and then embedding it in a Markov Chain Monte Carlo method, we can highly efficiently sample from the posterior, by replacing both the high-dimensional prior and the expensive forward map. We prove that the proposed methodology converges to the true posterior in the Wasserstein-1 distance and that sampling from the latent space is equivalent to sampling in the high-dimensional space in a weak sense. The method is showcased on two test cases where we perform both state and parameter estimation simultaneously. The approach is shown to be up to two orders of magnitude more accurate than alternative approaches while also being up to two orders of magnitude computationally faster, in multiple test cases, including the important engineering setting of detecting leaks in pipelines.
The phenomenon of hysteresis is commonly observed in many UV thermal experiments involving unmodified or modified nucleic acids. In presence of hysteresis, the thermal curves are irreversible and demand a significant effort to produce the reaction-specific kinetic and thermodynamic parameters. In this article, we describe a unified statistical procedure to analyze such thermal curves. Our method applies to experiments with intramolecular as well as intermolecular reactions. More specifically, the proposed method allows one to handle the thermal curves for the formation of duplexes, triplexes, and various quadruplexes in exactly the same way. The proposed method uses a local polynomial regression for finding the smoothed thermal curves and calculating their slopes. This method is more flexible and easy to implement than the least squares polynomial smoothing which is currently almost universally used for such purposes. Full analyses of the curves including computation of kinetic and thermodynamic parameters can be done using freely available statistical software. In the end, we illustrate our method by analyzing irreversible curves encountered in the formations of a G-quadruplex and an LNA-modified parallel duplex.
Causality can be described in terms of a structural causal model (SCM) that carries information on the variables of interest and their mechanistic relations. For most processes of interest the underlying SCM will only be partially observable, thus causal inference tries to leverage any exposed information. Graph neural networks (GNN) as universal approximators on structured input pose a viable candidate for causal learning, suggesting a tighter integration with SCM. To this effect we present a theoretical analysis from first principles that establishes a novel connection between GNN and SCM while providing an extended view on general neural-causal models. We then establish a new model class for GNN-based causal inference that is necessary and sufficient for causal effect identification. Our empirical illustration on simulations and standard benchmarks validate our theoretical proofs.
Graph Neural Networks (GNNs) have received considerable attention on graph-structured data learning for a wide variety of tasks. The well-designed propagation mechanism which has been demonstrated effective is the most fundamental part of GNNs. Although most of GNNs basically follow a message passing manner, litter effort has been made to discover and analyze their essential relations. In this paper, we establish a surprising connection between different propagation mechanisms with a unified optimization problem, showing that despite the proliferation of various GNNs, in fact, their proposed propagation mechanisms are the optimal solution optimizing a feature fitting function over a wide class of graph kernels with a graph regularization term. Our proposed unified optimization framework, summarizing the commonalities between several of the most representative GNNs, not only provides a macroscopic view on surveying the relations between different GNNs, but also further opens up new opportunities for flexibly designing new GNNs. With the proposed framework, we discover that existing works usually utilize naive graph convolutional kernels for feature fitting function, and we further develop two novel objective functions considering adjustable graph kernels showing low-pass or high-pass filtering capabilities respectively. Moreover, we provide the convergence proofs and expressive power comparisons for the proposed models. Extensive experiments on benchmark datasets clearly show that the proposed GNNs not only outperform the state-of-the-art methods but also have good ability to alleviate over-smoothing, and further verify the feasibility for designing GNNs with our unified optimization framework.