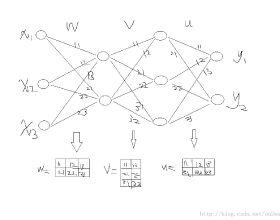
A Deep Neural Network (DNN) is a composite function of vector-valued functions, and in order to train a DNN, it is necessary to calculate the gradient of the loss function with respect to all parameters. This calculation can be a non-trivial task because the loss function of a DNN is a composition of several nonlinear functions, each with numerous parameters. The Backpropagation (BP) algorithm leverages the composite structure of the DNN to efficiently compute the gradient. As a result, the number of layers in the network does not significantly impact the complexity of the calculation. The objective of this paper is to express the gradient of the loss function in terms of a matrix multiplication using the Jacobian operator. This can be achieved by considering the total derivative of each layer with respect to its parameters and expressing it as a Jacobian matrix. The gradient can then be represented as the matrix product of these Jacobian matrices. This approach is valid because the chain rule can be applied to a composition of vector-valued functions, and the use of Jacobian matrices allows for the incorporation of multiple inputs and outputs. By providing concise mathematical justifications, the results can be made understandable and useful to a broad audience from various disciplines.
相關內容
This paper presents a new methodology to alleviate the fundamental trade-off between accuracy and latency in spiking neural networks (SNNs). The approach involves decoding confidence information over time from the SNN outputs and using it to develop a decision-making agent that can dynamically determine when to terminate each inference. The proposed method, Dynamic Confidence, provides several significant benefits to SNNs. 1. It can effectively optimize latency dynamically at runtime, setting it apart from many existing low-latency SNN algorithms. Our experiments on CIFAR-10 and ImageNet datasets have demonstrated an average 40% speedup across eight different settings after applying Dynamic Confidence. 2. The decision-making agent in Dynamic Confidence is straightforward to construct and highly robust in parameter space, making it extremely easy to implement. 3. The proposed method enables visualizing the potential of any given SNN, which sets a target for current SNNs to approach. For instance, if an SNN can terminate at the most appropriate time point for each input sample, a ResNet-50 SNN can achieve an accuracy as high as 82.47% on ImageNet within just 4.71 time steps on average. Unlocking the potential of SNNs needs a highly-reliable decision-making agent to be constructed and fed with a high-quality estimation of ground truth. In this regard, Dynamic Confidence represents a meaningful step toward realizing the potential of SNNs.
Backpropagation algorithm has been widely used as a mainstream learning procedure for neural networks in the past decade, and has played a significant role in the development of deep learning. However, there exist some limitations associated with this algorithm, such as getting stuck in local minima and experiencing vanishing/exploding gradients, which have led to questions about its biological plausibility. To address these limitations, alternative algorithms to backpropagation have been preliminarily explored, with the Forward-Forward (FF) algorithm being one of the most well-known. In this paper we propose a new learning framework for neural networks, namely Cascaded Forward (CaFo) algorithm, which does not rely on BP optimization as that in FF. Unlike FF, our framework directly outputs label distributions at each cascaded block, which does not require generation of additional negative samples and thus leads to a more efficient process at both training and testing. Moreover, in our framework each block can be trained independently, so it can be easily deployed into parallel acceleration systems. The proposed method is evaluated on four public image classification benchmarks, and the experimental results illustrate significant improvement in prediction accuracy in comparison with the baseline.
Deep Neural Networks (DNNs) have obtained impressive performance across tasks, however they still remain as black boxes, e.g., hard to theoretically analyze. At the same time, Polynomial Networks (PNs) have emerged as an alternative method with a promising performance and improved interpretability but have yet to reach the performance of the powerful DNN baselines. In this work, we aim to close this performance gap. We introduce a class of PNs, which are able to reach the performance of ResNet across a range of six benchmarks. We demonstrate that strong regularization is critical and conduct an extensive study of the exact regularization schemes required to match performance. To further motivate the regularization schemes, we introduce D-PolyNets that achieve a higher-degree of expansion than previously proposed polynomial networks. D-PolyNets are more parameter-efficient while achieving a similar performance as other polynomial networks. We expect that our new models can lead to an understanding of the role of elementwise activation functions (which are no longer required for training PNs). The source code is available at //github.com/grigorisg9gr/regularized_polynomials.
The Black-Scholes (B-S) equation has been recently extended as a kind of tempered time-fractional B-S equations, which become an interesting mathematical model in option pricing. In this study, we provide a fast numerical method to approximate the solution of the tempered time-fractional B-S model. To achieve high-order accuracy in space and overcome the weak initial singularity of the solution, we combine the compact operator with a tempered L1 approximation with nonuniform time steps to yield the numerical scheme. The convergence of the proposed difference scheme is proved to be unconditionally stable. Moreover, the kernel function in tempered Caputo fractional derivative is approximated by sum-of-exponentials, which leads to a fast unconditional stable compact difference method that reduces the computational cost. Finally, numerical results demonstrate the effectiveness of the proposed methods.
Knowledge distillation (KD) has shown very promising capabilities in transferring learning representations from large models (teachers) to small models (students). However, as the capacity gap between students and teachers becomes larger, existing KD methods fail to achieve better results. Our work shows that the `prior knowledge' is vital to KD, especially when applying large teachers. Particularly, we propose the dynamic prior knowledge (DPK), which integrates part of teacher's features as the prior knowledge before the feature distillation. This means that our method also takes the teacher's feature as `input', not just `target'. Besides, we dynamically adjust the ratio of the prior knowledge during the training phase according to the feature gap, thus guiding the student in an appropriate difficulty. To evaluate the proposed method, we conduct extensive experiments on two image classification benchmarks (i.e. CIFAR100 and ImageNet) and an object detection benchmark (i.e. MS COCO. The results demonstrate the superiority of our method in performance under varying settings. Besides, our DPK makes the performance of the student model positively correlated with that of the teacher model, which means that we can further boost the accuracy of students by applying larger teachers. More importantly, DPK provides a fast solution in teacher model selection for any given model.
Correlated outcomes are common in many practical problems. In some settings, one outcome is of particular interest, and others are auxiliary. To leverage information shared by all the outcomes, traditional multi-task learning (MTL) minimizes an averaged loss function over all the outcomes, which may lead to biased estimation for the target outcome, especially when the MTL model is mis-specified. In this work, based on a decomposition of estimation bias into two types, within-subspace and against-subspace, we develop a robust transfer learning approach to estimating a high-dimensional linear decision rule for the outcome of interest with the presence of auxiliary outcomes. The proposed method includes an MTL step using all outcomes to gain efficiency, and a subsequent calibration step using only the outcome of interest to correct both types of biases. We show that the final estimator can achieve a lower estimation error than the one using only the single outcome of interest. Simulations and real data analysis are conducted to justify the superiority of the proposed method.
High-dimensional data can often display heterogeneity due to heteroscedastic variance or inhomogeneous covariate effects. Penalized quantile and expectile regression methods offer useful tools to detect heteroscedasticity in high-dimensional data. The former is computationally challenging due to the non-smooth nature of the check loss, and the latter is sensitive to heavy-tailed error distributions. In this paper, we propose and study (penalized) robust expectile regression (retire), with a focus on iteratively reweighted $\ell_1$-penalization which reduces the estimation bias from $\ell_1$-penalization and leads to oracle properties. Theoretically, we establish the statistical properties of the retire estimator under two regimes: (i) low-dimensional regime in which $d \ll n$; (ii) high-dimensional regime in which $s\ll n\ll d$ with $s$ denoting the number of significant predictors. In the high-dimensional setting, we carefully characterize the solution path of the iteratively reweighted $\ell_1$-penalized retire estimation, adapted from the local linear approximation algorithm for folded-concave regularization. Under a mild minimum signal strength condition, we show that after as many as $\log(\log d)$ iterations the final iterate enjoys the oracle convergence rate. At each iteration, the weighted $\ell_1$-penalized convex program can be efficiently solved by a semismooth Newton coordinate descent algorithm. Numerical studies demonstrate the competitive performance of the proposed procedure compared with either non-robust or quantile regression based alternatives.
We study the computational complexity of multi-stage robust optimization problems. Such problems are formulated with alternating min/max quantifiers and therefore naturally fall into a higher stage of the polynomial hierarchy. Despite this, almost no hardness results with respect to the polynomial hierarchy are known. In this work, we examine the hardness of robust two-stage adjustable and robust recoverable optimization with budgeted uncertainty sets. Our main technical contribution is the introduction of a technique tailored to prove $\Sigma^p_3$-hardness of such problems. We highlight a difference between continuous and discrete budgeted uncertainty: In the discrete case, indeed a wide range of problems becomes complete for the third stage of the polynomial hierarchy; in particular, this applies to the TSP, independent set, and vertex cover problems. However, in the continuous case this does not happen and problems remain in the first stage of the hierarchy. Finally, if we allow the uncertainty to not only affect the objective, but also multiple constraints, then this distinction disappears and even in the continuous case we encounter hardness for the third stage of the hierarchy. This shows that even robust problems which are already NP-complete can still exhibit a significant computational difference between column-wise and row-wise uncertainty.
This paper focuses on the expected difference in borrower's repayment when there is a change in the lender's credit decisions. Classical estimators overlook the confounding effects and hence the estimation error can be magnificent. As such, we propose another approach to construct the estimators such that the error can be greatly reduced. The proposed estimators are shown to be unbiased, consistent, and robust through a combination of theoretical analysis and numerical testing. Moreover, we compare the power of estimating the causal quantities between the classical estimators and the proposed estimators. The comparison is tested across a wide range of models, including linear regression models, tree-based models, and neural network-based models, under different simulated datasets that exhibit different levels of causality, different degrees of nonlinearity, and different distributional properties. Most importantly, we apply our approaches to a large observational dataset provided by a global technology firm that operates in both the e-commerce and the lending business. We find that the relative reduction of estimation error is strikingly substantial if the causal effects are accounted for correctly.
Over the past few years, we have seen fundamental breakthroughs in core problems in machine learning, largely driven by advances in deep neural networks. At the same time, the amount of data collected in a wide array of scientific domains is dramatically increasing in both size and complexity. Taken together, this suggests many exciting opportunities for deep learning applications in scientific settings. But a significant challenge to this is simply knowing where to start. The sheer breadth and diversity of different deep learning techniques makes it difficult to determine what scientific problems might be most amenable to these methods, or which specific combination of methods might offer the most promising first approach. In this survey, we focus on addressing this central issue, providing an overview of many widely used deep learning models, spanning visual, sequential and graph structured data, associated tasks and different training methods, along with techniques to use deep learning with less data and better interpret these complex models --- two central considerations for many scientific use cases. We also include overviews of the full design process, implementation tips, and links to a plethora of tutorials, research summaries and open-sourced deep learning pipelines and pretrained models, developed by the community. We hope that this survey will help accelerate the use of deep learning across different scientific domains.