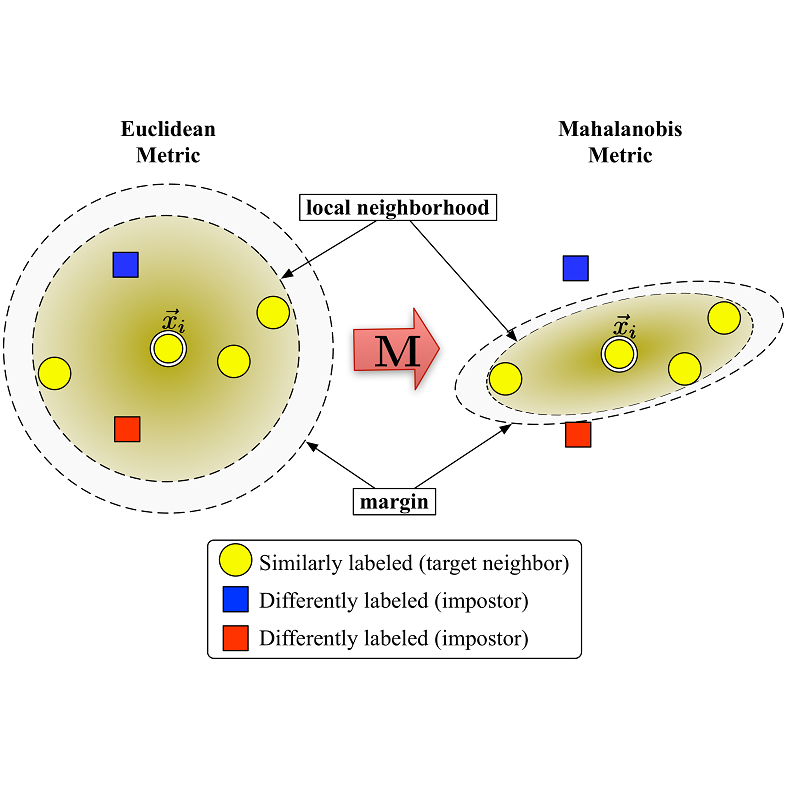
We explore the metric and preference learning problem in Hilbert spaces. We obtain a novel representer theorem for the simultaneous task of metric and preference learning. Our key observation is that the representer theorem can be formulated with respect to the norm induced by the inner product inherent in the problem structure. Additionally, we demonstrate how our framework can be applied to the task of metric learning from triplet comparisons and show that it leads to a simple and self-contained representer theorem for this task. In the case of Reproducing Kernel Hilbert Spaces (RKHS), we demonstrate that the solution to the learning problem can be expressed using kernel terms, akin to classical representer theorems.
相關內容
This paper studies robust nonparametric regression, in which an adversarial attacker can modify the values of up to $q$ samples from a training dataset of size $N$. Our initial solution is an M-estimator based on Huber loss minimization. Compared with simple kernel regression, i.e. the Nadaraya-Watson estimator, this method can significantly weaken the impact of malicious samples on the regression performance. We provide the convergence rate as well as the corresponding minimax lower bound. The result shows that, with proper bandwidth selection, $\ell_\infty$ error is minimax optimal. The $\ell_2$ error is optimal if $q\lesssim \sqrt{N/\ln^2 N}$, but is suboptimal with larger $q$. The reason is that this estimator is vulnerable if there are many attacked samples concentrating in a small region. To address this issue, we propose a correction method by projecting the initial estimate to the space of Lipschitz functions. The final estimate is nearly minimax optimal for arbitrary $q$, up to a $\ln N$ factor.
This paper introduces a matrix quantile factor model for matrix-valued data with a low-rank structure. We estimate the row and column factor spaces via minimizing the empirical check loss function over all panels. We show the estimates converge at rate $1/\min\{\sqrt{p_1p_2}, \sqrt{p_2T},$ $\sqrt{p_1T}\}$ in average Frobenius norm, where $p_1$, $p_2$ and $T$ are the row dimensionality, column dimensionality and length of the matrix sequence. This rate is faster than that of the quantile estimates via ``flattening" the matrix model into a large vector model. Smoothed estimates are given and their central limit theorems are derived under some mild condition. We provide three consistent criteria to determine the pair of row and column factor numbers. Extensive simulation studies and an empirical study justify our theory.
In this paper, we consider the problem of learning a linear regression model on a data domain of interest (target) given few samples. To aid learning, we are provided with a set of pre-trained regression models that are trained on potentially different data domains (sources). Assuming a representation structure for the data generating linear models at the sources and the target domains, we propose a representation transfer based learning method for constructing the target model. The proposed scheme is comprised of two phases: (i) utilizing the different source representations to construct a representation that is adapted to the target data, and (ii) using the obtained model as an initialization to a fine-tuning procedure that re-trains the entire (over-parameterized) regression model on the target data. For each phase of the training method, we provide excess risk bounds for the learned model compared to the true data generating target model. The derived bounds show a gain in sample complexity for our proposed method compared to the baseline method of not leveraging source representations when achieving the same excess risk, therefore, theoretically demonstrating the effectiveness of transfer learning for linear regression.
We discuss a federated learned compression problem, where the goal is to learn a compressor from real-world data which is scattered across clients and may be statistically heterogeneous, yet share a common underlying representation. We propose a distributed source model that encompasses both characteristics, and naturally suggests a compressor architecture that uses analysis and synthesis transforms shared by clients. Inspired by personalized federated learning methods, we employ an entropy model that is personalized to each client. This allows for a global latent space to be learned across clients, and personalized entropy models that adapt to the clients' latent distributions. We show empirically that this strategy outperforms solely local methods, which indicates that learned compression also benefits from a shared global representation in statistically heterogeneous federated settings.
This paper investigates the relationship between the universal approximation property of deep neural networks and topological characteristics of datasets. Our primary contribution is to introduce data topology-dependent upper bounds on the network width. Specifically, we first show that a three-layer neural network, applying a ReLU activation function and max pooling, can be designed to approximate an indicator function over a compact set, one that is encompassed by a tight convex polytope. This is then extended to a simplicial complex, deriving width upper bounds based on its topological structure. Further, we calculate upper bounds in relation to the Betti numbers of select topological spaces. Finally, we prove the universal approximation property of three-layer ReLU networks using our topological approach. We also verify that gradient descent converges to the network structure proposed in our study.
In this paper, we propose a new model for forecasting time series data distributed on a matrix-shaped spatial grid, using the historical spatio-temporal data together with auxiliary vector-valued time series data. We model the matrix time series as an auto-regressive process, where a future matrix is jointly predicted by the historical values of the matrix time series as well as an auxiliary vector time series. The matrix predictors are associated with row/column-specific autoregressive matrix coefficients that map the predictors to the future matrices via a bi-linear transformation. The vector predictors are mapped to matrices by taking mode product with a 3D coefficient tensor. Given the high dimensionality of the tensor coefficient and the underlying spatial structure of the data, we propose to estimate the tensor coefficient by estimating one functional coefficient for each covariate, with 2D input domain, from a Reproducing Kernel Hilbert Space. We jointly estimate the autoregressive matrix coefficients and the functional coefficients under a penalized maximum likelihood estimation framework, and couple it with an alternating minimization algorithm. Large sample asymptotics of the estimators are established and performances of the model are validated with extensive simulation studies and a real data application to forecast the global total electron content distributions.
We consider the problem of explaining the predictions of graph neural networks (GNNs), which otherwise are considered as black boxes. Existing methods invariably focus on explaining the importance of graph nodes or edges but ignore the substructures of graphs, which are more intuitive and human-intelligible. In this work, we propose a novel method, known as SubgraphX, to explain GNNs by identifying important subgraphs. Given a trained GNN model and an input graph, our SubgraphX explains its predictions by efficiently exploring different subgraphs with Monte Carlo tree search. To make the tree search more effective, we propose to use Shapley values as a measure of subgraph importance, which can also capture the interactions among different subgraphs. To expedite computations, we propose efficient approximation schemes to compute Shapley values for graph data. Our work represents the first attempt to explain GNNs via identifying subgraphs explicitly and directly. Experimental results show that our SubgraphX achieves significantly improved explanations, while keeping computations at a reasonable level.
Federated learning enables multiple parties to collaboratively train a machine learning model without communicating their local data. A key challenge in federated learning is to handle the heterogeneity of local data distribution across parties. Although many studies have been proposed to address this challenge, we find that they fail to achieve high performance in image datasets with deep learning models. In this paper, we propose MOON: model-contrastive federated learning. MOON is a simple and effective federated learning framework. The key idea of MOON is to utilize the similarity between model representations to correct the local training of individual parties, i.e., conducting contrastive learning in model-level. Our extensive experiments show that MOON significantly outperforms the other state-of-the-art federated learning algorithms on various image classification tasks.
Self-supervised learning has been widely used to obtain transferrable representations from unlabeled images. Especially, recent contrastive learning methods have shown impressive performances on downstream image classification tasks. While these contrastive methods mainly focus on generating invariant global representations at the image-level under semantic-preserving transformations, they are prone to overlook spatial consistency of local representations and therefore have a limitation in pretraining for localization tasks such as object detection and instance segmentation. Moreover, aggressively cropped views used in existing contrastive methods can minimize representation distances between the semantically different regions of a single image. In this paper, we propose a spatially consistent representation learning algorithm (SCRL) for multi-object and location-specific tasks. In particular, we devise a novel self-supervised objective that tries to produce coherent spatial representations of a randomly cropped local region according to geometric translations and zooming operations. On various downstream localization tasks with benchmark datasets, the proposed SCRL shows significant performance improvements over the image-level supervised pretraining as well as the state-of-the-art self-supervised learning methods.
Graph representation learning is to learn universal node representations that preserve both node attributes and structural information. The derived node representations can be used to serve various downstream tasks, such as node classification and node clustering. When a graph is heterogeneous, the problem becomes more challenging than the homogeneous graph node learning problem. Inspired by the emerging information theoretic-based learning algorithm, in this paper we propose an unsupervised graph neural network Heterogeneous Deep Graph Infomax (HDGI) for heterogeneous graph representation learning. We use the meta-path structure to analyze the connections involving semantics in heterogeneous graphs and utilize graph convolution module and semantic-level attention mechanism to capture local representations. By maximizing local-global mutual information, HDGI effectively learns high-level node representations that can be utilized in downstream graph-related tasks. Experiment results show that HDGI remarkably outperforms state-of-the-art unsupervised graph representation learning methods on both classification and clustering tasks. By feeding the learned representations into a parametric model, such as logistic regression, we even achieve comparable performance in node classification tasks when comparing with state-of-the-art supervised end-to-end GNN models.