Functional principal component analysis (FPCA) has played an important role in the development of functional time series analysis. This note investigates how FPCA can be used to analyze cointegrated functional time series and proposes a modification of FPCA as a novel statistical tool. Our modified FPCA not only provides an asymptotically more efficient estimator of the cointegrating vectors, but also leads to novel FPCA-based tests for examining essential properties of cointegrated functional time series.
相關內容
Computing properties of molecular systems rely on estimating expectations of the (unnormalized) Boltzmann distribution. Molecular dynamics (MD) is a broadly adopted technique to approximate such quantities. However, stable simulations rely on very small integration time-steps ($10^{-15}\,\mathrm{s}$), whereas convergence of some moments, e.g. binding free energy or rates, might rely on sampling processes on time-scales as long as $10^{-1}\, \mathrm{s}$, and these simulations must be repeated for every molecular system independently. Here, we present Implict Transfer Operator (ITO) Learning, a framework to learn surrogates of the simulation process with multiple time-resolutions. We implement ITO with denoising diffusion probabilistic models with a new SE(3) equivariant architecture and show the resulting models can generate self-consistent stochastic dynamics across multiple time-scales, even when the system is only partially observed. Finally, we present a coarse-grained CG-SE3-ITO model which can quantitatively model all-atom molecular dynamics using only coarse molecular representations. As such, ITO provides an important step towards multiple time- and space-resolution acceleration of MD.
Datasets with sheer volume have been generated from fields including computer vision, medical imageology, and astronomy whose large-scale and high-dimensional properties hamper the implementation of classical statistical models. To tackle the computational challenges, one of the efficient approaches is subsampling which draws subsamples from the original large datasets according to a carefully-design task-specific probability distribution to form an informative sketch. The computation cost is reduced by applying the original algorithm to the substantially smaller sketch. Previous studies associated with subsampling focused on non-regularized regression from the computational efficiency and theoretical guarantee perspectives, such as ordinary least square regression and logistic regression. In this article, we introduce a randomized algorithm under the subsampling scheme for the Elastic-net regression which gives novel insights into L1-norm regularized regression problem. To effectively conduct consistency analysis, a smooth approximation technique based on alpha absolute function is firstly employed and theoretically verified. The concentration bounds and asymptotic normality for the proposed randomized algorithm are then established under mild conditions. Moreover, an optimal subsampling probability is constructed according to A-optimality. The effectiveness of the proposed algorithm is demonstrated upon synthetic and real data datasets.
Legal properties involve reasoning about data values and time. Metric first-order temporal logic (MFOTL) provides a rich formalism for specifying legal properties. While MFOTL has been successfully used for verifying legal properties over operational systems via runtime monitoring, no solution exists for MFOTL-based verification in early-stage system development captured by requirements. Given a legal property and system requirements, both formalized in MFOTL, the compliance of the property can be verified on the requirements via satisfiability checking. In this paper, we propose a practical, sound, and complete (within a given bound) satisfiability checking approach for MFOTL. The approach, based on satisfiability modulo theories (SMT), employs a counterexample-guided strategy to incrementally search for a satisfying solution. We implemented our approach using the Z3 SMT solver and evaluated it on five case studies spanning the healthcare, business administration, banking and aviation domains. Our results indicate that our approach can efficiently determine whether legal properties of interest are met, or generate counterexamples that lead to compliance violations.
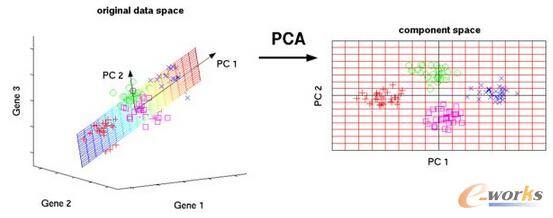
Principal Component Analysis (PCA) is a pivotal technique in the fields of machine learning and data analysis. In this study, we present a novel approach for privacy-preserving PCA using an approximate numerical arithmetic homomorphic encryption scheme. We build our method upon a proposed PCA routine known as the PowerMethod, which takes the covariance matrix as input and produces an approximate eigenvector corresponding to the first principal component of the dataset. Our method surpasses previous approaches (e.g., Pandas CSCML 21) in terms of efficiency, accuracy, and scalability. To achieve such efficiency and accuracy, we have implemented the following optimizations: (i) We optimized a homomorphic matrix multiplication technique (Jiang et al. SIGSAC 2018) that will play a crucial role in the computation of the covariance matrix. (ii) We devised an efficient homomorphic circuit for computing the covariance matrix homomorphically. (iii) We designed a novel and efficient homomorphic circuit for the PowerMethod that incorporates a systematic strategy for homomorphic vector normalization enhancing both its accuracy and practicality. Our matrix multiplication optimization reduces the minimum rotation key space required for a $128\times 128$ homomorphic matrix multiplication by up to 64\%, enabling more extensive parallel computation of multiple matrix multiplication instances. Our homomorphic covariance matrix computation method manages to compute the covariance matrix of the MNIST dataset ($60000\times 256$) in 51 minutes. Our privacy-preserving PCA scheme based on our new homomorphic PowerMethod circuit successfully computes the top 8 principal components of datasets such as MNIST and Fashion-MNIST in approximately 1 hour, achieving an r2 accuracy of 0.7 to 0.9, achieving an average speed improvement of over 4 times and offers higher accuracy compared to previous approaches.
Independent Component Analysis (ICA) aims to recover independent latent variables from observed mixtures thereof. Causal Representation Learning (CRL) aims instead to infer causally related (thus often statistically dependent) latent variables, together with the unknown graph encoding their causal relationships. We introduce an intermediate problem termed Causal Component Analysis (CauCA). CauCA can be viewed as a generalization of ICA, modelling the causal dependence among the latent components, and as a special case of CRL. In contrast to CRL, it presupposes knowledge of the causal graph, focusing solely on learning the unmixing function and the causal mechanisms. Any impossibility results regarding the recovery of the ground truth in CauCA also apply for CRL, while possibility results may serve as a stepping stone for extensions to CRL. We characterize CauCA identifiability from multiple datasets generated through different types of interventions on the latent causal variables. As a corollary, this interventional perspective also leads to new identifiability results for nonlinear ICA -- a special case of CauCA with an empty graph -- requiring strictly fewer datasets than previous results. We introduce a likelihood-based approach using normalizing flows to estimate both the unmixing function and the causal mechanisms, and demonstrate its effectiveness through extensive synthetic experiments in the CauCA and ICA setting.
This paper examines robust functional data analysis for discretely observed data, where the underlying process encompasses various distributions, such as heavy tail, skewness, or contaminations. We propose a unified robust concept of functional mean, covariance, and principal component analysis, while existing methods and definitions often differ from one another or only address fully observed functions (the ``ideal'' case). Specifically, the robust functional mean can deviate from its non-robust counterpart and is estimated using robust local linear regression. Moreover, we define a new robust functional covariance that shares useful properties with the classic version. Importantly, this covariance yields the robust version of Karhunen--Lo\`eve decomposition and corresponding principal components beneficial for dimension reduction. The theoretical results of the robust functional mean, covariance, and eigenfunction estimates, based on pooling discretely observed data (ranging from sparse to dense), are established and aligned with their non-robust counterparts. The newly-proposed perturbation bounds for estimated eigenfunctions, with indexes allowed to grow with sample size, lay the foundation for further modeling based on robust functional principal component analysis.
Consistency learning plays a crucial role in semi-supervised medical image segmentation as it enables the effective utilization of limited annotated data while leveraging the abundance of unannotated data. The effectiveness and efficiency of consistency learning are challenged by prediction diversity and training stability, which are often overlooked by existing studies. Meanwhile, the limited quantity of labeled data for training often proves inadequate for formulating intra-class compactness and inter-class discrepancy of pseudo labels. To address these issues, we propose a self-aware and cross-sample prototypical learning method (SCP-Net) to enhance the diversity of prediction in consistency learning by utilizing a broader range of semantic information derived from multiple inputs. Furthermore, we introduce a self-aware consistency learning method that exploits unlabeled data to improve the compactness of pseudo labels within each class. Moreover, a dual loss re-weighting method is integrated into the cross-sample prototypical consistency learning method to improve the reliability and stability of our model. Extensive experiments on ACDC dataset and PROMISE12 dataset validate that SCP-Net outperforms other state-of-the-art semi-supervised segmentation methods and achieves significant performance gains compared to the limited supervised training. Our code will come soon.
Federated Learning (FL) is a distributed learning paradigm that empowers edge devices to collaboratively learn a global model leveraging local data. Simulating FL on GPU is essential to expedite FL algorithm prototyping and evaluations. However, current FL frameworks overlook the disparity between algorithm simulation and real-world deployment, which arises from heterogeneous computing capabilities and imbalanced workloads, thus misleading evaluations of new algorithms. Additionally, they lack flexibility and scalability to accommodate resource-constrained clients. In this paper, we present FedHC, a scalable federated learning framework for heterogeneous and resource-constrained clients. FedHC realizes system heterogeneity by allocating a dedicated and constrained GPU resource budget to each client, and also simulates workload heterogeneity in terms of framework-provided runtime. Furthermore, we enhance GPU resource utilization for scalable clients by introducing a dynamic client scheduler, process manager, and resource-sharing mechanism. Our experiments demonstrate that FedHC has the capability to capture the influence of various factors on client execution time. Moreover, despite resource constraints for each client, FedHC achieves state-of-the-art efficiency compared to existing frameworks without limits. When subjecting existing frameworks to the same resource constraints, FedHC achieves a 2.75x speedup. Code has been released on //github.com/if-lab-repository/FedHC.
Analyzing observational data from multiple sources can be useful for increasing statistical power to detect a treatment effect; however, practical constraints such as privacy considerations may restrict individual-level information sharing across data sets. This paper develops federated methods that only utilize summary-level information from heterogeneous data sets. Our federated methods provide doubly-robust point estimates of treatment effects as well as variance estimates. We derive the asymptotic distributions of our federated estimators, which are shown to be asymptotically equivalent to the corresponding estimators from the combined, individual-level data. We show that to achieve these properties, federated methods should be adjusted based on conditions such as whether models are correctly specified and stable across heterogeneous data sets.
Graph convolutional networks (GCNs) have been successfully applied in node classification tasks of network mining. However, most of these models based on neighborhood aggregation are usually shallow and lack the "graph pooling" mechanism, which prevents the model from obtaining adequate global information. In order to increase the receptive field, we propose a novel deep Hierarchical Graph Convolutional Network (H-GCN) for semi-supervised node classification. H-GCN first repeatedly aggregates structurally similar nodes to hyper-nodes and then refines the coarsened graph to the original to restore the representation for each node. Instead of merely aggregating one- or two-hop neighborhood information, the proposed coarsening procedure enlarges the receptive field for each node, hence more global information can be learned. Comprehensive experiments conducted on public datasets demonstrate the effectiveness of the proposed method over the state-of-art methods. Notably, our model gains substantial improvements when only a few labeled samples are provided.