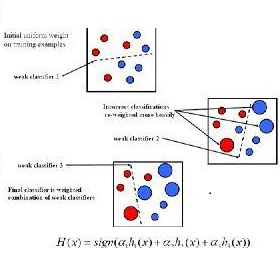
The principle of boosting in supervised learning involves combining multiple weak classifiers to obtain a stronger classifier. AdaBoost has the reputation to be a perfect example of this approach. We have previously shown that AdaBoost is not truly an optimization algorithm. This paper shows that AdaBoost is an algorithm in name only, as the resulting combination of weak classifiers can be explicitly calculated using a truth table. This study is carried out by considering a problem with two classes and is illustrated by the particular case of three binary classifiers and presents results in comparison with those from the implementation of AdaBoost algorithm of the Python library scikit-learn.
相關內容
Emerging from the monolithic pairwise attention mechanism in conventional Transformer models, there is a growing interest in leveraging sparse interactions that align more closely with biological principles. Approaches including the Set Transformer and the Perceiver employ cross-attention consolidated with a latent space that forms an attention bottleneck with limited capacity. Building upon recent neuroscience studies of Global Workspace Theory and associative memory, we propose the Associative Transformer (AiT). AiT induces low-rank explicit memory that serves as both priors to guide bottleneck attention in the shared workspace and attractors within associative memory of a Hopfield network. Through joint end-to-end training, these priors naturally develop module specialization, each contributing a distinct inductive bias to form attention bottlenecks. A bottleneck can foster competition among inputs for writing information into the memory. We show that AiT is a sparse representation learner, learning distinct priors through the bottlenecks that are complexity-invariant to input quantities and dimensions. AiT demonstrates its superiority over methods such as the Set Transformer, Vision Transformer, and Coordination in various vision tasks.
Proximal causal learning is a promising framework for identifying the causal effect under the existence of unmeasured confounders. Within this framework, the doubly robust (DR) estimator was derived and has shown its effectiveness in estimation, especially when the model assumption is violated. However, the current form of the DR estimator is restricted to binary treatments, while the treatment can be continuous in many real-world applications. The primary obstacle to continuous treatments resides in the delta function present in the original DR estimator, making it infeasible in causal effect estimation and introducing a heavy computational burden in nuisance function estimation. To address these challenges, we propose a kernel-based DR estimator that can well handle continuous treatments. Equipped with its smoothness, we show that its oracle form is a consistent approximation of the influence function. Further, we propose a new approach to efficiently solve the nuisance functions. We then provide a comprehensive convergence analysis in terms of the mean square error. We demonstrate the utility of our estimator on synthetic datasets and real-world applications.
Virtual element methods (VEMs) without extrinsic stabilization in arbitrary degree of polynomial are developed for second order elliptic problems, including a nonconforming VEM and a conforming VEM in arbitrary dimension. The key is to construct local $H(\textrm{div})$-conforming macro finite element spaces such that the associated $L^2$ projection of the gradient of virtual element functions is computable, and the $L^2$ projector has a uniform lower bound on the gradient of virtual element function spaces in $L^2$ norm. Optimal error estimates are derived for these VEMs. Numerical experiments are provided to test the VEMs without extrinsic stabilization.
To exploit the expressivity of being able to refer to the type of types, such as for large elimination, dependent type systems will either employ a universe hierarchy or else contend with an inconsistent type-in-type rule. However, these are not be the only possible options. Taking inspiration from Stratified System F, we introduce Stratified Type Theory (StraTT), where rather than stratifying universes by levels, we stratify typing judgements and restrict the domain of dependent function types to some fixed level strictly lower than that of the overall type. Even in the presence of type-in-type, this restriction suffices to enforce consistency of the system. We explore the expressivity of several extensions atop this design. First, the subsystem subStraTT employs McBride's crude-but-effective stratification (also known as displacement) as a simple form of level polymorphism where top-level definitions can be displaced uniformly to any higher level as needed, which is valid due to level cumulativity and plays well with stratified judgements. Second, to recover some expressivity lost due to the restriction on dependent function domains, the full StraTT system includes a separate nondependent function type with floating domains, whose level instead matches that of the overall type. Finally, we have implemented a prototype type checker for StraTT extended with datatypes along with a small type checked core library. While it's possible to show that the subsystem is consistent, showing consistency for the full system with floating nondependent functions remains open. Nevertheless, we believe that the full system is also consistent and have mechanized a syntactic proof of subject reduction. Furthermore, we use our implementation to investigate various well-known type-theoretic type-in-type paradoxes. These examples all fail to type check in expected ways as evidence towards consistency.
A hypothesis class admits a sample compression scheme, if for every sample labeled by a hypothesis from the class, it is possible to retain only a small subsample, using which the labels on the entire sample can be inferred. The size of the compression scheme is an upper bound on the size of the subsample produced. Every learnable binary hypothesis class (which must necessarily have finite VC dimension) admits a sample compression scheme of size only a finite function of its VC dimension, independent of the sample size. For multiclass hypothesis classes, the analog of VC dimension is the DS dimension. We show that the analogous statement pertaining to sample compression is not true for multiclass hypothesis classes: every learnable multiclass hypothesis class, which must necessarily have finite DS dimension, does not admit a sample compression scheme of size only a finite function of its DS dimension.
This article unifies and generalizes fundamental results related to $n$-process asynchronous crash-prone distributed computing. More precisely, it proves that for every $0\leq k \leq n$, assuming that process failures occur only before the number of participating processes bypasses a predefined threshold that equals $n-k$ (a participating process is a process that has executed at least one statement of its code), an asynchronous algorithm exists that solves consensus for $n$ processes in the presence of $f$ crash failures if and only if $f \leq k$. In a very simple and interesting way, the "extreme" case $k=0$ boils down to the celebrated FLP impossibility result (1985, 1987). Moreover, the second extreme case, namely $k=n$, captures the celebrated mutual exclusion result by E.W. Dijkstra (1965) that states that mutual exclusion can be solved for $n$ processes in an asynchronous read/write shared memory system where any number of processes may crash (but only) before starting to participate in the algorithm (that is, participation is not required, but once a process starts participating it may not fail). More generally, the possibility/impossibility stated above demonstrates that more failures can be tolerated when they occur earlier in the computation (hence the title).
The introduction of the generative adversarial imitation learning (GAIL) algorithm has spurred the development of scalable imitation learning approaches using deep neural networks. Many of the algorithms that followed used a similar procedure, combining on-policy actor-critic algorithms with inverse reinforcement learning. More recently there have been an even larger breadth of approaches, most of which use off-policy algorithms. However, with the breadth of algorithms, everything from datasets to base reinforcement learning algorithms to evaluation settings can vary, making it difficult to fairly compare them. In this work we re-implement 6 different IL algorithms, updating 3 of them to be off-policy, base them on a common off-policy algorithm (SAC), and evaluate them on a widely-used expert trajectory dataset (D4RL) for the most common benchmark (MuJoCo). After giving all algorithms the same hyperparameter optimisation budget, we compare their results for a range of expert trajectories. In summary, GAIL, with all of its improvements, consistently performs well across a range of sample sizes, AdRIL is a simple contender that performs well with one important hyperparameter to tune, and behavioural cloning remains a strong baseline when data is more plentiful.
The conjoining of dynamical systems and deep learning has become a topic of great interest. In particular, neural differential equations (NDEs) demonstrate that neural networks and differential equation are two sides of the same coin. Traditional parameterised differential equations are a special case. Many popular neural network architectures, such as residual networks and recurrent networks, are discretisations. NDEs are suitable for tackling generative problems, dynamical systems, and time series (particularly in physics, finance, ...) and are thus of interest to both modern machine learning and traditional mathematical modelling. NDEs offer high-capacity function approximation, strong priors on model space, the ability to handle irregular data, memory efficiency, and a wealth of available theory on both sides. This doctoral thesis provides an in-depth survey of the field. Topics include: neural ordinary differential equations (e.g. for hybrid neural/mechanistic modelling of physical systems); neural controlled differential equations (e.g. for learning functions of irregular time series); and neural stochastic differential equations (e.g. to produce generative models capable of representing complex stochastic dynamics, or sampling from complex high-dimensional distributions). Further topics include: numerical methods for NDEs (e.g. reversible differential equations solvers, backpropagation through differential equations, Brownian reconstruction); symbolic regression for dynamical systems (e.g. via regularised evolution); and deep implicit models (e.g. deep equilibrium models, differentiable optimisation). We anticipate this thesis will be of interest to anyone interested in the marriage of deep learning with dynamical systems, and hope it will provide a useful reference for the current state of the art.
Contrastive learning models have achieved great success in unsupervised visual representation learning, which maximize the similarities between feature representations of different views of the same image, while minimize the similarities between feature representations of views of different images. In text summarization, the output summary is a shorter form of the input document and they have similar meanings. In this paper, we propose a contrastive learning model for supervised abstractive text summarization, where we view a document, its gold summary and its model generated summaries as different views of the same mean representation and maximize the similarities between them during training. We improve over a strong sequence-to-sequence text generation model (i.e., BART) on three different summarization datasets. Human evaluation also shows that our model achieves better faithfulness ratings compared to its counterpart without contrastive objectives.
We advocate the use of implicit fields for learning generative models of shapes and introduce an implicit field decoder for shape generation, aimed at improving the visual quality of the generated shapes. An implicit field assigns a value to each point in 3D space, so that a shape can be extracted as an iso-surface. Our implicit field decoder is trained to perform this assignment by means of a binary classifier. Specifically, it takes a point coordinate, along with a feature vector encoding a shape, and outputs a value which indicates whether the point is outside the shape or not. By replacing conventional decoders by our decoder for representation learning and generative modeling of shapes, we demonstrate superior results for tasks such as shape autoencoding, generation, interpolation, and single-view 3D reconstruction, particularly in terms of visual quality.