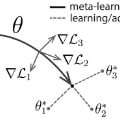
In this paper, we study the generalization properties of Model-Agnostic Meta-Learning (MAML) algorithms for supervised learning problems. We focus on the setting in which we train the MAML model over $m$ tasks, each with $n$ data points, and characterize its generalization error from two points of view: First, we assume the new task at test time is one of the training tasks, and we show that, for strongly convex objective functions, the expected excess population loss is bounded by ${\mathcal{O}}(1/mn)$. Second, we consider the MAML algorithm's generalization to an unseen task and show that the resulting generalization error depends on the total variation distance between the underlying distributions of the new task and the tasks observed during the training process. Our proof techniques rely on the connections between algorithmic stability and generalization bounds of algorithms. In particular, we propose a new definition of stability for meta-learning algorithms, which allows us to capture the role of both the number of tasks $m$ and number of samples per task $n$ on the generalization error of MAML.
相關內容
We study meta-learning in Markov Decision Processes (MDP) with linear transition models in the undiscounted episodic setting. Under a task sharedness metric based on model proximity we study task families characterized by a distribution over models specified by a bias term and a variance component. We then propose BUC-MatrixRL, a version of the UC-Matrix RL algorithm, and show it can meaningfully leverage a set of sampled training tasks to quickly solve a test task sampled from the same task distribution by learning an estimator of the bias parameter of the task distribution. The analysis leverages and extends results in the learning to learn linear regression and linear bandit setting to the more general case of MDP's with linear transition models. We prove that compared to learning the tasks in isolation, BUC-Matrix RL provides significant improvements in the transfer regret for high bias low variance task distributions.
We introduce a tensor-based model of shared representation for meta-learning from a diverse set of tasks. Prior works on learning linear representations for meta-learning assume that there is a common shared representation across different tasks, and do not consider the additional task-specific observable side information. In this work, we model the meta-parameter through an order-$3$ tensor, which can adapt to the observed task features of the task. We propose two methods to estimate the underlying tensor. The first method solves a tensor regression problem and works under natural assumptions on the data generating process. The second method uses the method of moments under additional distributional assumptions and has an improved sample complexity in terms of the number of tasks. We also focus on the meta-test phase, and consider estimating task-specific parameters on a new task. Substituting the estimated tensor from the first step allows us estimating the task-specific parameters with very few samples of the new task, thereby showing the benefits of learning tensor representations for meta-learning. Finally, through simulation and several real-world datasets, we evaluate our methods and show that it improves over previous linear models of shared representations for meta-learning.
This dissertation studies a fundamental open challenge in deep learning theory: why do deep networks generalize well even while being overparameterized, unregularized and fitting the training data to zero error? In the first part of the thesis, we will empirically study how training deep networks via stochastic gradient descent implicitly controls the networks' capacity. Subsequently, to show how this leads to better generalization, we will derive {\em data-dependent} {\em uniform-convergence-based} generalization bounds with improved dependencies on the parameter count. Uniform convergence has in fact been the most widely used tool in deep learning literature, thanks to its simplicity and generality. Given its popularity, in this thesis, we will also take a step back to identify the fundamental limits of uniform convergence as a tool to explain generalization. In particular, we will show that in some example overparameterized settings, {\em any} uniform convergence bound will provide only a vacuous generalization bound. With this realization in mind, in the last part of the thesis, we will change course and introduce an {\em empirical} technique to estimate generalization using unlabeled data. Our technique does not rely on any notion of uniform-convergece-based complexity and is remarkably precise. We will theoretically show why our technique enjoys such precision. We will conclude by discussing how future work could explore novel ways to incorporate distributional assumptions in generalization bounds (such as in the form of unlabeled data) and explore other tools to derive bounds, perhaps by modifying uniform convergence or by developing completely new tools altogether.
When and why can a neural network be successfully trained? This article provides an overview of optimization algorithms and theory for training neural networks. First, we discuss the issue of gradient explosion/vanishing and the more general issue of undesirable spectrum, and then discuss practical solutions including careful initialization and normalization methods. Second, we review generic optimization methods used in training neural networks, such as SGD, adaptive gradient methods and distributed methods, and theoretical results for these algorithms. Third, we review existing research on the global issues of neural network training, including results on bad local minima, mode connectivity, lottery ticket hypothesis and infinite-width analysis.
Model-agnostic meta-learners aim to acquire meta-learned parameters from similar tasks to adapt to novel tasks from the same distribution with few gradient updates. With the flexibility in the choice of models, those frameworks demonstrate appealing performance on a variety of domains such as few-shot image classification and reinforcement learning. However, one important limitation of such frameworks is that they seek a common initialization shared across the entire task distribution, substantially limiting the diversity of the task distributions that they are able to learn from. In this paper, we augment MAML with the capability to identify the mode of tasks sampled from a multimodal task distribution and adapt quickly through gradient updates. Specifically, we propose a multimodal MAML (MMAML) framework, which is able to modulate its meta-learned prior parameters according to the identified mode, allowing more efficient fast adaptation. We evaluate the proposed model on a diverse set of few-shot learning tasks, including regression, image classification, and reinforcement learning. The results not only demonstrate the effectiveness of our model in modulating the meta-learned prior in response to the characteristics of tasks but also show that training on a multimodal distribution can produce an improvement over unimodal training.
Gradient-based meta-learning techniques are both widely applicable and proficient at solving challenging few-shot learning and fast adaptation problems. However, they have the practical difficulties of operating in high-dimensional parameter spaces in extreme low-data regimes. We show that it is possible to bypass these limitations by learning a low-dimensional latent generative representation of model parameters and performing gradient-based meta-learning in this space with latent embedding optimization (LEO), effectively decoupling the gradient-based adaptation procedure from the underlying high-dimensional space of model parameters. Our evaluation shows that LEO can achieve state-of-the-art performance on the competitive 5-way 1-shot miniImageNet classification task.
We propose a new method of estimation in topic models, that is not a variation on the existing simplex finding algorithms, and that estimates the number of topics K from the observed data. We derive new finite sample minimax lower bounds for the estimation of A, as well as new upper bounds for our proposed estimator. We describe the scenarios where our estimator is minimax adaptive. Our finite sample analysis is valid for any number of documents (n), individual document length (N_i), dictionary size (p) and number of topics (K), and both p and K are allowed to increase with n, a situation not handled well by previous analyses. We complement our theoretical results with a detailed simulation study. We illustrate that the new algorithm is faster and more accurate than the current ones, although we start out with a computational and theoretical disadvantage of not knowing the correct number of topics K, while we provide the competing methods with the correct value in our simulations.
Meta-learning enables a model to learn from very limited data to undertake a new task. In this paper, we study the general meta-learning with adversarial samples. We present a meta-learning algorithm, ADML (ADversarial Meta-Learner), which leverages clean and adversarial samples to optimize the initialization of a learning model in an adversarial manner. ADML leads to the following desirable properties: 1) it turns out to be very effective even in the cases with only clean samples; 2) it is model-agnostic, i.e., it is compatible with any learning model that can be trained with gradient descent; and most importantly, 3) it is robust to adversarial samples, i.e., unlike other meta-learning methods, it only leads to a minor performance degradation when there are adversarial samples. We show via extensive experiments that ADML delivers the state-of-the-art performance on two widely-used image datasets, MiniImageNet and CIFAR100, in terms of both accuracy and robustness.
We develop an approach to risk minimization and stochastic optimization that provides a convex surrogate for variance, allowing near-optimal and computationally efficient trading between approximation and estimation error. Our approach builds off of techniques for distributionally robust optimization and Owen's empirical likelihood, and we provide a number of finite-sample and asymptotic results characterizing the theoretical performance of the estimator. In particular, we show that our procedure comes with certificates of optimality, achieving (in some scenarios) faster rates of convergence than empirical risk minimization by virtue of automatically balancing bias and variance. We give corroborating empirical evidence showing that in practice, the estimator indeed trades between variance and absolute performance on a training sample, improving out-of-sample (test) performance over standard empirical risk minimization for a number of classification problems.
In multi-task learning, a learner is given a collection of prediction tasks and needs to solve all of them. In contrast to previous work, which required that annotated training data is available for all tasks, we consider a new setting, in which for some tasks, potentially most of them, only unlabeled training data is provided. Consequently, to solve all tasks, information must be transferred between tasks with labels and tasks without labels. Focusing on an instance-based transfer method we analyze two variants of this setting: when the set of labeled tasks is fixed, and when it can be actively selected by the learner. We state and prove a generalization bound that covers both scenarios and derive from it an algorithm for making the choice of labeled tasks (in the active case) and for transferring information between the tasks in a principled way. We also illustrate the effectiveness of the algorithm by experiments on synthetic and real data.