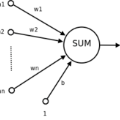
Time series of counts are frequently analyzed using generalized integer-valued autoregressive models with conditional heteroskedasticity (INGARCH). These models employ response functions to map a vector of past observations and past conditional expectations to the conditional expectation of the present observation. In this paper, it is shown how INGARCH models can be combined with artificial neural network (ANN) response functions to obtain a class of nonlinear INGARCH models. The ANN framework allows for the interpretation of many existing INGARCH models as a degenerate version of a corresponding neural model. Details on maximum likelihood estimation, marginal effects and confidence intervals are given. The empirical analysis of time series of bounded and unbounded counts reveals that the neural INGARCH models are able to outperform reasonable degenerate competitor models in terms of the information loss.
相關內容
Existing results for the estimation of the L\'evy measure are mostly limited to the onedimensional setting. We apply the spectral method to multidimensional L\'evy processes in order to construct a nonparametric estimator for the multivariate jump distribution. We prove convergence rates for the uniform estimation error under both a low- and a high-frequency observation regime. The method is robust to various dependence structures. Along the way, we present a uniform risk bound for the multivariate empirical characteristic function and its partial derivatives. The method is illustrated with simulation examples.
Counterfactual Explanations are becoming a de-facto standard in post-hoc interpretable machine learning. For a given classifier and an instance classified in an undesired class, its counterfactual explanation corresponds to small perturbations of that instance that allows changing the classification outcome. This work aims to leverage Counterfactual Explanations to detect the important decision boundaries of a pre-trained black-box model. This information is used to build a supervised discretization of the features in the dataset with a tunable granularity. Using the discretized dataset, an optimal Decision Tree can be trained that resembles the black-box model, but that is interpretable and compact. Numerical results on real-world datasets show the effectiveness of the approach in terms of accuracy and sparsity.
Applications of CAR for balancing continuous covariates remain comparatively rare, especially in multi-treatment clinical trials, and the theoretical properties of multi-treatment CAR have remained largely elusive for decades. In this paper, we consider a general framework of CAR procedures for multi-treatment clinal trials which can balance general covariate features, such as quadratic and interaction terms which can be discrete, continuous, and mixing. We show that under widely satisfied conditions the proposed procedures have superior balancing properties; in particular, the convergence rate of imbalance vectors can attain the best rate $O_P(1)$ for discrete covariates, continuous covariates, or combinations of both discrete and continuous covariates, and at the same time, the convergence rate of the imbalance of unobserved covariates is $O_P(\sqrt n)$, where $n$ is the sample size. The general framework unifies many existing methods and related theories, introduces a much broader class of new and useful CAR procedures, and provides new insights and a complete picture of the properties of CAR procedures. The favorable balancing properties lead to the precision of the treatment effect test in the presence of a heteroscedastic linear model with dependent covariate features. As an application, the properties of the test of treatment effect with unobserved covariates are studied under the CAR procedures, and consistent tests are proposed so that the test has an asymptotic precise type I error even if the working model is wrong and covariates are unobserved in the analysis.
Weighting methods in causal inference have been widely used to achieve a desirable level of covariate balancing. However, the existing weighting methods have desirable theoretical properties only when a certain model, either the propensity score or outcome regression model, is correctly specified. In addition, the corresponding estimators do not behave well for finite samples due to large variance even when the model is correctly specified. In this paper, we consider to use the integral probability metric (IPM), which is a metric between two probability measures, for covariate balancing. Optimal weights are determined so that weighted empirical distributions for the treated and control groups have the smallest IPM value for a given set of discriminators. We prove that the corresponding estimator can be consistent without correctly specifying any model (neither the propensity score nor the outcome regression model). In addition, we empirically show that our proposed method outperforms existing weighting methods with large margins for finite samples.
Bayesian probabilistic numerical methods for numerical integration offer significant advantages over their non-Bayesian counterparts: they can encode prior information about the integrand, and can quantify uncertainty over estimates of an integral. However, the most popular algorithm in this class, Bayesian quadrature, is based on Gaussian process models and is therefore associated with a high computational cost. To improve scalability, we propose an alternative approach based on Bayesian neural networks which we call Bayesian Stein networks. The key ingredients are a neural network architecture based on Stein operators, and an approximation of the Bayesian posterior based on the Laplace approximation. We show that this leads to orders of magnitude speed-ups on the popular Genz functions benchmark, and on challenging problems arising in the Bayesian analysis of dynamical systems, and the prediction of energy production for a large-scale wind farm.
This paper aims at obtaining, by means of integral transforms, analytical approximations in short times of solutions to boundary value problems for the one-dimensional reaction-diffusion equation with constant coefficients. The general form of the equation is considered on a bounded generic interval and the three classical types of boundary conditions, i.e., Dirichlet as well as Neumann and mixed boundary conditions are considered in a unified way. The Fourier and Laplace integral transforms are successively applied and an exact solution is obtained in the Laplace domain. This operational solution is proven to be the accurate Laplace transform of the infinite series obtained by the Fourier decomposition method and presented in the literature as solutions to this type of problem. On the basis of this unified operational solution, four cases are distinguished where innovative formulas expressing consistent analytical approximations in short time limits are derived with respect to the behavior of the solution at the boundaries. Compared to the infinite series solutions, the analytical approximations may open new perspectives and applications, among which can be noted the improvement of numerical efficiency in simulations of one-dimensional moving boundary problems, such as in Stefan models.
Large language models (LLMs) have initiated a paradigm shift in transfer learning. In contrast to the classic pretraining-then-finetuning procedure, in order to use LLMs for downstream prediction tasks, one only needs to provide a few demonstrations, known as in-context examples, without adding more or updating existing model parameters. This in-context learning (ICL) capabilities of LLMs is intriguing, and it is not yet fully understood how pretrained LLMs acquire such capabilities. In this paper, we investigate the reason why a transformer-based language model can accomplish in-context learning after pre-training on a general language corpus by proposing one hypothesis that LLMs can simulate kernel regression algorithms when faced with in-context examples. More concretely, we first prove that Bayesian inference on in-context prompts can be asymptotically understood as kernel regression $\hat y = \frac{\sum_i y_i K(x, x_i)}{\sum_i K(x, x_i)}$ as the number of in-context demonstrations grows. Then, we empirically investigate the in-context behaviors of language models. We find that during ICL, the attentions and hidden features in LLMs match the behaviors of a kernel regression. Finally, our theory provides insights on multiple phenomena observed in ICL field: why retrieving demonstrative samples similar to test sample can help, why ICL performance is sensitive to the output formats, and why ICL accuracy benefits from selecting in-distribution and representative samples. We will make our code available to the research community following publication.
Analysis of networks that evolve dynamically requires the joint modelling of individual snapshots and time dynamics. This paper proposes a new flexible two-way heterogeneity model towards this goal. The new model equips each node of the network with two heterogeneity parameters, one to characterize the propensity to form ties with other nodes statically and the other to differentiate the tendency to retain existing ties over time. With $n$ observed networks each having $p$ nodes, we develop a new asymptotic theory for the maximum likelihood estimation of $2p$ parameters when $np\rightarrow \infty$. We overcome the global non-convexity of the negative log-likelihood function by the virtue of its local convexity, and propose a novel method of moment estimator as the initial value for a simple algorithm that leads to the consistent local maximum likelihood estimator (MLE). To establish the upper bounds for the estimation error of the MLE, we derive a new uniform deviation bound, which is of independent interest. The theory of the model and its usefulness are further supported by extensive simulation and a data analysis examining social interactions of ants.
Large language models (LLMs) have shown remarkable capabilities in language understanding and generation. However, such impressive capability typically comes with a substantial model size, which presents significant challenges in both the deployment, inference, and training stages. With LLM being a general-purpose task solver, we explore its compression in a task-agnostic manner, which aims to preserve the multi-task solving and language generation ability of the original LLM. One challenge to achieving this is the enormous size of the training corpus of LLM, which makes both data transfer and model post-training over-burdensome. Thus, we tackle the compression of LLMs within the bound of two constraints: being task-agnostic and minimizing the reliance on the original training dataset. Our method, named LLM-Pruner, adopts structural pruning that selectively removes non-critical coupled structures based on gradient information, maximally preserving the majority of the LLM's functionality. To this end, the performance of pruned models can be efficiently recovered through tuning techniques, LoRA, in merely 3 hours, requiring only 50K data. We validate the LLM-Pruner on three LLMs, including LLaMA, Vicuna, and ChatGLM, and demonstrate that the compressed models still exhibit satisfactory capabilities in zero-shot classification and generation. The code is available at: //github.com/horseee/LLM-Pruner
Evidence Networks can enable Bayesian model comparison when state-of-the-art methods (e.g. nested sampling) fail and even when likelihoods or priors are intractable or unknown. Bayesian model comparison, i.e. the computation of Bayes factors or evidence ratios, can be cast as an optimization problem. Though the Bayesian interpretation of optimal classification is well-known, here we change perspective and present classes of loss functions that result in fast, amortized neural estimators that directly estimate convenient functions of the Bayes factor. This mitigates numerical inaccuracies associated with estimating individual model probabilities. We introduce the leaky parity-odd power (l-POP) transform, leading to the novel ``l-POP-Exponential'' loss function. We explore neural density estimation for data probability in different models, showing it to be less accurate and scalable than Evidence Networks. Multiple real-world and synthetic examples illustrate that Evidence Networks are explicitly independent of dimensionality of the parameter space and scale mildly with the complexity of the posterior probability density function. This simple yet powerful approach has broad implications for model inference tasks. As an application of Evidence Networks to real-world data we compute the Bayes factor for two models with gravitational lensing data of the Dark Energy Survey. We briefly discuss applications of our methods to other, related problems of model comparison and evaluation in implicit inference settings.