We provide initial seedings to the Quick Shift clustering algorithm, which approximate the locally high-density regions of the data. Such seedings act as more stable and expressive cluster-cores than the singleton modes found by Quick Shift. We establish statistical consistency guarantees for this modification. We then show strong clustering performance on real datasets as well as promising applications to image segmentation.
相關內容
With the rapid increase of large-scale, real-world datasets, it becomes critical to address the problem of long-tailed data distribution (i.e., a few classes account for most of the data, while most classes are under-represented). Existing solutions typically adopt class re-balancing strategies such as re-sampling and re-weighting based on the number of observations for each class. In this work, we argue that as the number of samples increases, the additional benefit of a newly added data point will diminish. We introduce a novel theoretical framework to measure data overlap by associating with each sample a small neighboring region rather than a single point. The effective number of samples is defined as the volume of samples and can be calculated by a simple formula $(1-\beta^{n})/(1-\beta)$, where $n$ is the number of samples and $\beta \in [0,1)$ is a hyperparameter. We design a re-weighting scheme that uses the effective number of samples for each class to re-balance the loss, thereby yielding a class-balanced loss. Comprehensive experiments are conducted on artificially induced long-tailed CIFAR datasets and large-scale datasets including ImageNet and iNaturalist. Our results show that when trained with the proposed class-balanced loss, the network is able to achieve significant performance gains on long-tailed datasets.
Object detectors tend to perform poorly in new or open domains, and require exhaustive yet costly annotations from fully labeled datasets. We aim at benefiting from several datasets with different categories but without additional labelling, not only to increase the number of categories detected, but also to take advantage from transfer learning and to enhance domain independence. Our dataset merging procedure starts with training several initial Faster R-CNN on the different datasets while considering the complementary datasets' images for domain adaptation. Similarly to self-training methods, the predictions of these initial detectors mitigate the missing annotations on the complementary datasets. The final OMNIA Faster R-CNN is trained with all categories on the union of the datasets enriched by predictions. The joint training handles unsafe targets with a new classification loss called SoftSig in a softly supervised way. Experimental results show that in the case of fashion detection for images in the wild, merging Modanet with COCO increases the final performance from 45.5% to 57.4%. Applying our soft distillation to the task of detection with domain shift on Cityscapes enables to beat the state-of-the-art by 5.3 points. We hope that our methodology could unlock object detection for real-world applications without immense datasets.
We present a generalization of the Cauchy/Lorentzian, Geman-McClure, Welsch/Leclerc, generalized Charbonnier, Charbonnier/pseudo-Huber/L1-L2, and L2 loss functions. By introducing robustness as a continous parameter, our loss function allows algorithms built around robust loss minimization to be generalized, which improves performance on basic vision tasks such as registration and clustering. Interpreting our loss as the negative log of a univariate density yields a general probability distribution that includes normal and Cauchy distributions as special cases. This probabilistic interpretation enables the training of neural networks in which the robustness of the loss automatically adapts itself during training, which improves performance on learning-based tasks such as generative image synthesis and unsupervised monocular depth estimation, without requiring any manual parameter tuning.
Novel neural models have been proposed in recent years for learning under domain shift. Most models, however, only evaluate on a single task, on proprietary datasets, or compare to weak baselines, which makes comparison of models difficult. In this paper, we re-evaluate classic general-purpose bootstrapping approaches in the context of neural networks under domain shifts vs. recent neural approaches and propose a novel multi-task tri-training method that reduces the time and space complexity of classic tri-training. Extensive experiments on two benchmarks are negative: while our novel method establishes a new state-of-the-art for sentiment analysis, it does not fare consistently the best. More importantly, we arrive at the somewhat surprising conclusion that classic tri-training, with some additions, outperforms the state of the art. We conclude that classic approaches constitute an important and strong baseline.
The Normalized Cut (NCut) objective function, widely used in data clustering and image segmentation, quantifies the cost of graph partitioning in a way that biases clusters or segments that are balanced towards having lower values than unbalanced partitionings. However, this bias is so strong that it avoids any singleton partitions, even when vertices are very weakly connected to the rest of the graph. Motivated by the B\"uhler-Hein family of balanced cut costs, we propose the family of Compassionately Conservative Balanced (CCB) Cut costs, which are indexed by a parameter that can be used to strike a compromise between the desire to avoid too many singleton partitions and the notion that all partitions should be balanced. We show that CCB-Cut minimization can be relaxed into an orthogonally constrained $\ell_{\tau}$-minimization problem that coincides with the problem of computing Piecewise Flat Embeddings (PFE) for one particular index value, and we present an algorithm for solving the relaxed problem by iteratively minimizing a sequence of reweighted Rayleigh quotients (IRRQ). Using images from the BSDS500 database, we show that image segmentation based on CCB-Cut minimization provides better accuracy with respect to ground truth and greater variability in region size than NCut-based image segmentation.
This work presents a region-growing image segmentation approach based on superpixel decomposition. From an initial contour-constrained over-segmentation of the input image, the image segmentation is achieved by iteratively merging similar superpixels into regions. This approach raises two key issues: (1) how to compute the similarity between superpixels in order to perform accurate merging and (2) in which order those superpixels must be merged together. In this perspective, we firstly introduce a robust adaptive multi-scale superpixel similarity in which region comparisons are made both at content and common border level. Secondly, we propose a global merging strategy to efficiently guide the region merging process. Such strategy uses an adpative merging criterion to ensure that best region aggregations are given highest priorities. This allows to reach a final segmentation into consistent regions with strong boundary adherence. We perform experiments on the BSDS500 image dataset to highlight to which extent our method compares favorably against other well-known image segmentation algorithms. The obtained results demonstrate the promising potential of the proposed approach.
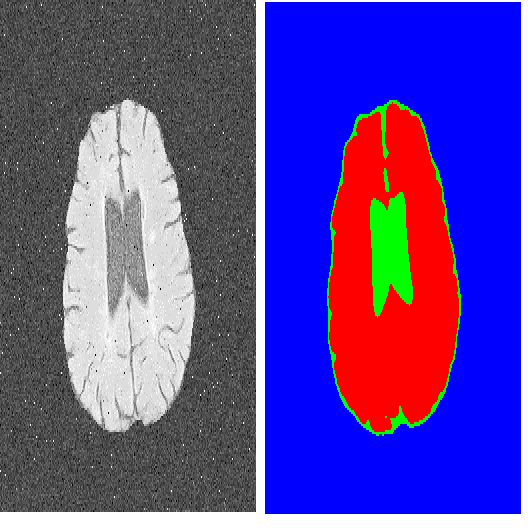
We propose an Active Learning approach to image segmentation that exploits geometric priors to streamline the annotation process. We demonstrate this for both background-foreground and multi-class segmentation tasks in 2D images and 3D image volumes. Our approach combines geometric smoothness priors in the image space with more traditional uncertainty measures to estimate which pixels or voxels are most in need of annotation. For multi-class settings, we additionally introduce two novel criteria for uncertainty. In the 3D case, we use the resulting uncertainty measure to show the annotator voxels lying on the same planar patch, which makes batch annotation much easier than if they were randomly distributed in the volume. The planar patch is found using a branch-and-bound algorithm that finds a patch with the most informative instances. We evaluate our approach on Electron Microscopy and Magnetic Resonance image volumes, as well as on regular images of horses and faces. We demonstrate a substantial performance increase over state-of-the-art approaches.
Amortized inference has led to efficient approximate inference for large datasets. The quality of posterior inference is largely determined by two factors: a) the ability of the variational distribution to model the true posterior and b) the capacity of the recognition network to generalize inference over all datapoints. We analyze approximate inference in variational autoencoders in terms of these factors. We find that suboptimal inference is often due to amortizing inference rather than the limited complexity of the approximating distribution. We show that this is due partly to the generator learning to accommodate the choice of approximation. Furthermore, we show that the parameters used to increase the expressiveness of the approximation play a role in generalizing inference rather than simply improving the complexity of the approximation.
We develop an approach to risk minimization and stochastic optimization that provides a convex surrogate for variance, allowing near-optimal and computationally efficient trading between approximation and estimation error. Our approach builds off of techniques for distributionally robust optimization and Owen's empirical likelihood, and we provide a number of finite-sample and asymptotic results characterizing the theoretical performance of the estimator. In particular, we show that our procedure comes with certificates of optimality, achieving (in some scenarios) faster rates of convergence than empirical risk minimization by virtue of automatically balancing bias and variance. We give corroborating empirical evidence showing that in practice, the estimator indeed trades between variance and absolute performance on a training sample, improving out-of-sample (test) performance over standard empirical risk minimization for a number of classification problems.
Robust estimation is much more challenging in high dimensions than it is in one dimension: Most techniques either lead to intractable optimization problems or estimators that can tolerate only a tiny fraction of errors. Recent work in theoretical computer science has shown that, in appropriate distributional models, it is possible to robustly estimate the mean and covariance with polynomial time algorithms that can tolerate a constant fraction of corruptions, independent of the dimension. However, the sample and time complexity of these algorithms is prohibitively large for high-dimensional applications. In this work, we address both of these issues by establishing sample complexity bounds that are optimal, up to logarithmic factors, as well as giving various refinements that allow the algorithms to tolerate a much larger fraction of corruptions. Finally, we show on both synthetic and real data that our algorithms have state-of-the-art performance and suddenly make high-dimensional robust estimation a realistic possibility.