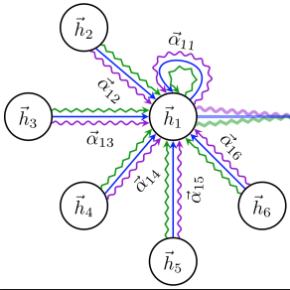
Distributed Constraint Optimization Problems (DCOPs) are an important subclass of combinatorial optimization problems, where information and controls are distributed among multiple autonomous agents. Previously, Machine Learning (ML) has been largely applied to solve combinatorial optimization problems by learning effective heuristics. However, existing ML-based heuristic methods are often not generalizable to different search algorithms. Most importantly, these methods usually require full knowledge about the problems to be solved, which are not suitable for distributed settings where centralization is not realistic due to geographical limitations or privacy concerns. To address the generality issue, we propose a novel directed acyclic graph representation schema for DCOPs and leverage the Graph Attention Networks (GATs) to embed graph representations. Our model, GAT-PCM, is then pretrained with optimally labelled data in an offline manner, so as to construct effective heuristics to boost a broad range of DCOP algorithms where evaluating the quality of a partial assignment is critical, such as local search or backtracking search. Furthermore, to enable decentralized model inference, we propose a distributed embedding schema of GAT-PCM where each agent exchanges only embedded vectors, and show its soundness and complexity. Finally, we demonstrate the effectiveness of our model by combining it with a local search or a backtracking search algorithm. Extensive empirical evaluations indicate that the GAT-PCM-boosted algorithms significantly outperform the state-of-the-art methods in various benchmarks. The pretrained model is available at //github.com/dyc941126/GAT-PCM.
相關內容
In this paper, we present a consensus-based decentralized multi-robot approach to reconstruct a discrete distribution of features, modeled as an occupancy grid map, that represent information contained in a bounded planar environment, such as visual cues used for navigation or semantic labels associated with object detection. The robots explore the environment according to a random walk modeled by a discrete-time discrete-state (DTDS) Markov chain and estimate the feature distribution from their own measurements and the estimates communicated by neighboring robots, using a distributed Chernoff fusion protocol. We prove that under this decentralized fusion protocol, each robot's feature distribution converges to the actual distribution in an almost sure sense. We verify this result in numerical simulations that show that the Hellinger distance between the estimated and actual feature distributions converges to zero over time for each robot. We also validate our strategy through Software-In-The-Loop (SITL) simulations of quadrotors that search a bounded square grid for a set of visual features distributed on a discretized circle.
Distributed Gaussian process (DGP) is a popular approach to scale GP to big data which divides the training data into some subsets, performs local inference for each partition, and aggregates the results to acquire global prediction. To combine the local predictions, the conditional independence assumption is used which basically means there is a perfect diversity between the subsets. Although it keeps the aggregation tractable, it is often violated in practice and generally yields poor results. In this paper, we propose a novel approach for aggregating the Gaussian experts' predictions by Gaussian graphical model (GGM) where the target aggregation is defined as an unobserved latent variable and the local predictions are the observed variables. We first estimate the joint distribution of latent and observed variables using the Expectation-Maximization (EM) algorithm. The interaction between experts can be encoded by the precision matrix of the joint distribution and the aggregated predictions are obtained based on the property of conditional Gaussian distribution. Using both synthetic and real datasets, our experimental evaluations illustrate that our new method outperforms other state-of-the-art DGP approaches.
Recently, Deep Neural Networks (DNNs) have recorded great success in handling medical and other complex classification tasks. However, as the sizes of a DNN model and the available dataset increase, the training process becomes more complex and computationally intensive, which usually takes a longer time to complete. In this work, we have proposed a generic full end-to-end hybrid parallelization approach combining both model and data parallelism for efficiently distributed and scalable training of DNN models. We have also proposed a Genetic Algorithm based heuristic resources allocation mechanism (GABRA) for optimal distribution of partitions on the available GPUs for computing performance optimization. We have applied our proposed approach to a real use case based on 3D Residual Attention Deep Neural Network (3D-ResAttNet) for efficient Alzheimer Disease (AD) diagnosis on multiple GPUs. The experimental evaluation shows that the proposed approach is efficient and scalable, which achieves almost linear speedup with little or no differences in accuracy performance when compared with the existing non-parallel DNN models.
Improving sample-efficiency and safety are crucial challenges when deploying reinforcement learning in high-stakes real world applications. We propose LAMBDA, a novel model-based approach for policy optimization in safety critical tasks modeled via constrained Markov decision processes. Our approach utilizes Bayesian world models, and harnesses the resulting uncertainty to maximize optimistic upper bounds on the task objective, as well as pessimistic upper bounds on the safety constraints. We demonstrate LAMBDA's state of the art performance on the Safety-Gym benchmark suite in terms of sample efficiency and constraint violation.
We consider information-theoretic bounds on expected generalization error for statistical learning problems in a networked setting. In this setting, there are $K$ nodes, each with its own independent dataset, and the models from each node have to be aggregated into a final centralized model. We consider both simple averaging of the models as well as more complicated multi-round algorithms. We give upper bounds on the expected generalization error for a variety of problems, such as those with Bregman divergence or Lipschitz continuous losses, that demonstrate an improved dependence of $1/K$ on the number of nodes. These "per node" bounds are in terms of the mutual information between the training dataset and the trained weights at each node, and are therefore useful in describing the generalization properties inherent to having communication or privacy constraints at each node.
Constrained optimization problems can be difficult because their search spaces have properties not conducive to search, e.g., multimodality, discontinuities, or deception. To address such difficulties, considerable research has been performed on creating novel evolutionary algorithms or specialized genetic operators. However, if the representation that defined the search space could be altered such that it only permitted valid solutions that satisfied the constraints, the task of finding the optimal would be made more feasible without any need for specialized optimization algorithms. We propose the use of a Variational Autoencoder to learn such representations. We present Constrained Optimization in Latent Space (COIL), which uses a VAE to generate a learned latent representation from a dataset comprising samples from the valid region of the search space according to a constraint, thus enabling the optimizer to find the objective in the new space defined by the learned representation. We investigate the value of this approach on different constraint types and for different numbers of variables. We show that, compared to an identical GA using a standard representation, COIL with its learned latent representation can satisfy constraints and find solutions with distance to objective up to two orders of magnitude closer.
The demand for artificial intelligence has grown significantly over the last decade and this growth has been fueled by advances in machine learning techniques and the ability to leverage hardware acceleration. However, in order to increase the quality of predictions and render machine learning solutions feasible for more complex applications, a substantial amount of training data is required. Although small machine learning models can be trained with modest amounts of data, the input for training larger models such as neural networks grows exponentially with the number of parameters. Since the demand for processing training data has outpaced the increase in computation power of computing machinery, there is a need for distributing the machine learning workload across multiple machines, and turning the centralized into a distributed system. These distributed systems present new challenges, first and foremost the efficient parallelization of the training process and the creation of a coherent model. This article provides an extensive overview of the current state-of-the-art in the field by outlining the challenges and opportunities of distributed machine learning over conventional (centralized) machine learning, discussing the techniques used for distributed machine learning, and providing an overview of the systems that are available.
Network embedding aims to learn a latent, low-dimensional vector representations of network nodes, effective in supporting various network analytic tasks. While prior arts on network embedding focus primarily on preserving network topology structure to learn node representations, recently proposed attributed network embedding algorithms attempt to integrate rich node content information with network topological structure for enhancing the quality of network embedding. In reality, networks often have sparse content, incomplete node attributes, as well as the discrepancy between node attribute feature space and network structure space, which severely deteriorates the performance of existing methods. In this paper, we propose a unified framework for attributed network embedding-attri2vec-that learns node embeddings by discovering a latent node attribute subspace via a network structure guided transformation performed on the original attribute space. The resultant latent subspace can respect network structure in a more consistent way towards learning high-quality node representations. We formulate an optimization problem which is solved by an efficient stochastic gradient descent algorithm, with linear time complexity to the number of nodes. We investigate a series of linear and non-linear transformations performed on node attributes and empirically validate their effectiveness on various types of networks. Another advantage of attri2vec is its ability to solve out-of-sample problems, where embeddings of new coming nodes can be inferred from their node attributes through the learned mapping function. Experiments on various types of networks confirm that attri2vec is superior to state-of-the-art baselines for node classification, node clustering, as well as out-of-sample link prediction tasks. The source code of this paper is available at //github.com/daokunzhang/attri2vec.
The field of Multi-Agent System (MAS) is an active area of research within Artificial Intelligence, with an increasingly important impact in industrial and other real-world applications. Within a MAS, autonomous agents interact to pursue personal interests and/or to achieve common objectives. Distributed Constraint Optimization Problems (DCOPs) have emerged as one of the prominent agent architectures to govern the agents' autonomous behavior, where both algorithms and communication models are driven by the structure of the specific problem. During the last decade, several extensions to the DCOP model have enabled them to support MAS in complex, real-time, and uncertain environments. This survey aims at providing an overview of the DCOP model, giving a classification of its multiple extensions and addressing both resolution methods and applications that find a natural mapping within each class of DCOPs. The proposed classification suggests several future perspectives for DCOP extensions, and identifies challenges in the design of efficient resolution algorithms, possibly through the adaptation of strategies from different areas.
In this paper, we study the optimal convergence rate for distributed convex optimization problems in networks. We model the communication restrictions imposed by the network as a set of affine constraints and provide optimal complexity bounds for four different setups, namely: the function $F(\xb) \triangleq \sum_{i=1}^{m}f_i(\xb)$ is strongly convex and smooth, either strongly convex or smooth or just convex. Our results show that Nesterov's accelerated gradient descent on the dual problem can be executed in a distributed manner and obtains the same optimal rates as in the centralized version of the problem (up to constant or logarithmic factors) with an additional cost related to the spectral gap of the interaction matrix. Finally, we discuss some extensions to the proposed setup such as proximal friendly functions, time-varying graphs, improvement of the condition numbers.