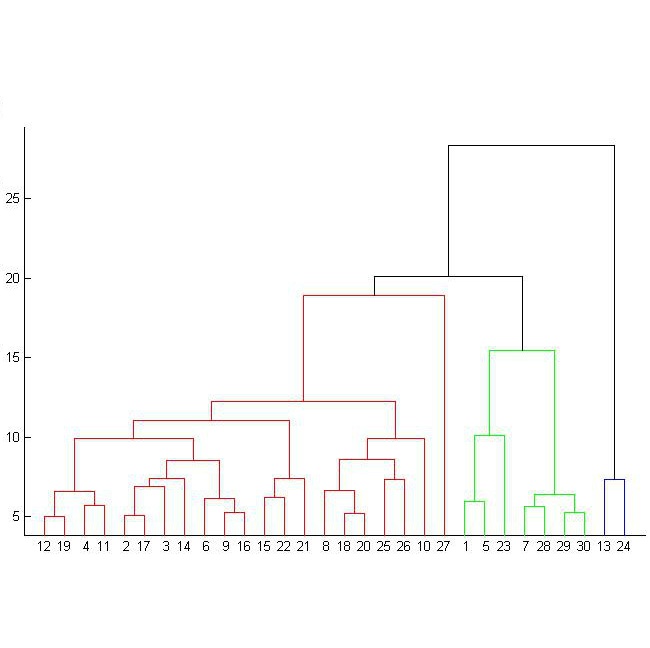
Despite much attention, the comparison of reduced-dimension representations of high-dimensional data remains a challenging problem in multiple fields, especially when representations remain high-dimensional compared to sample size. We offer a framework for evaluating the topological similarity of high-dimensional representations of very high-dimensional data, a regime where topological structure is more likely captured in the distribution of topological "noise" than a few prominent generators. Treating each representational map as a metric embedding, we compute the Vietoris-Rips persistence of its image. We then use the topological bootstrap to analyze the re-sampling stability of each representation, assigning a "prevalence score" for each nontrivial basis element of its persistence module. Finally, we compare the persistent homology of representations using a prevalence-weighted variant of the Wasserstein distance. Notably, our method is able to compare representations derived from different samples of the same distribution and, in particular, is not restricted to comparisons of graphs on the same vertex set. In addition, representations need not lie in the same metric space. We apply this analysis to a cross-sectional sample of representations of functional neuroimaging data in a large cohort and hierarchically cluster under the prevalence-weighted Wasserstein. We find that the ambient dimension of a representation is a stronger predictor of the number and stability of topological features than its decomposition rank. Our findings suggest that important topological information lies in repeatable, low-persistence homology generators, whose distributions capture important and interpretable differences between high-dimensional data representations.
相關內容
Multiscale problems are challenging for neural network-based discretizations of differential equations, such as physics-informed neural networks (PINNs). This can be (partly) attributed to the so-called spectral bias of neural networks. To improve the performance of PINNs for time-dependent problems, a combination of multifidelity stacking PINNs and domain decomposition-based finite basis PINNs are employed. In particular, to learn the high-fidelity part of the multifidelity model, a domain decomposition in time is employed. The performance is investigated for a pendulum and a two-frequency problem as well as the Allen-Cahn equation. It can be observed that the domain decomposition approach clearly improves the PINN and stacking PINN approaches.
In a network of reinforced stochastic processes, for certain values of the parameters, all the agents' inclinations synchronize and converge almost surely toward a certain random variable. The present work aims at clarifying when the agents can asymptotically polarize, i.e. when the common limit inclination can take the extreme values, 0 or 1, with probability zero, strictly positive, or equal to one. Moreover, we present a suitable technique to estimate this probability that, along with the theoretical results, has been framed in the more general setting of a class of martingales taking values in [0, 1] and following a specific dynamics.

We characterize structures such as monotonicity, convexity, and modality in smooth regression curves using persistent homology. Persistent homology is a key tool in topological data analysis that detects higher dimensional topological features such as connected components and holes (cycles or loops) in the data. In other words, persistent homology is a multiscale version of homology that characterizes sets based on the connected components and holes. We use super-level sets of functions to extract geometric features via persistent homology. In particular, we explore structures in regression curves via the persistent homology of super-level sets of a function, where the function of interest is - the first derivative of the regression function. In the course of this study, we extend an existing procedure of estimating the persistent homology for the first derivative of a regression function and establish its consistency. Moreover, as an application of the proposed methodology, we demonstrate that the persistent homology of the derivative of a function can reveal hidden structures in the function that are not visible from the persistent homology of the function itself. In addition, we also illustrate that the proposed procedure can be used to compare the shapes of two or more regression curves which is not possible merely from the persistent homology of the function itself.
We introduce a novel neuromorphic network architecture based on a lattice of exciton-polariton condensates, intricately interconnected and energized through non-resonant optical pumping. The network employs a binary framework, where each neuron, facilitated by the spatial coherence of pairwise coupled condensates, performs binary operations. This coherence, emerging from the ballistic propagation of polaritons, ensures efficient, network-wide communication. The binary neuron switching mechanism, driven by the nonlinear repulsion through the excitonic component of polaritons, offers computational efficiency and scalability advantages over continuous weight neural networks. Our network enables parallel processing, enhancing computational speed compared to sequential or pulse-coded binary systems. The system's performance was evaluated using the MNIST dataset for handwritten digit recognition, showcasing the potential to outperform existing polaritonic neuromorphic systems, as demonstrated by its impressive predicted classification accuracy of up to 97.5%.
We study knowable informational dependence between empirical questions, modeled as continuous functional dependence between variables in a topological setting. We also investigate epistemic independence in topological terms and show that it is compatible with functional (but non-continuous) dependence. We then proceed to study a stronger notion of knowability based on uniformly continuous dependence. On the technical logical side, we determine the complete logics of languages that combine general functional dependence, continuous dependence, and uniformly continuous dependence.
We study the convergence of stochastic gradient descent (SGD) for non-convex objective functions. We establish the local convergence with positive probability under the local \L{}ojasiewicz condition introduced by Chatterjee in \cite{chatterjee2022convergence} and an additional local structural assumption of the loss function landscape. A key component of our proof is to ensure that the whole trajectories of SGD stay inside the local region with a positive probability. We also provide examples of neural networks with finite widths such that our assumptions hold.
Recent extensive numerical experiments in high scale machine learning have allowed to uncover a quite counterintuitive phase transition, as a function of the ratio between the sample size and the number of parameters in the model. As the number of parameters $p$ approaches the sample size $n$, the generalisation error increases, but surprisingly, it starts decreasing again past the threshold $p=n$. This phenomenon, brought to the theoretical community attention in \cite{belkin2019reconciling}, has been thoroughly investigated lately, more specifically for simpler models than deep neural networks, such as the linear model when the parameter is taken to be the minimum norm solution to the least-squares problem, firstly in the asymptotic regime when $p$ and $n$ tend to infinity, see e.g. \cite{hastie2019surprises}, and recently in the finite dimensional regime and more specifically for linear models \cite{bartlett2020benign}, \cite{tsigler2020benign}, \cite{lecue2022geometrical}. In the present paper, we propose a finite sample analysis of non-linear models of \textit{ridge} type, where we investigate the \textit{overparametrised regime} of the double descent phenomenon for both the \textit{estimation problem} and the \textit{prediction} problem. Our results provide a precise analysis of the distance of the best estimator from the true parameter as well as a generalisation bound which complements recent works of \cite{bartlett2020benign} and \cite{chinot2020benign}. Our analysis is based on tools closely related to the continuous Newton method \cite{neuberger2007continuous} and a refined quantitative analysis of the performance in prediction of the minimum $\ell_2$-norm solution.
Unreliable predictions can occur when using artificial intelligence (AI) systems with negative consequences for downstream applications, particularly when employed for decision-making. Conformal prediction provides a model-agnostic framework for uncertainty quantification that can be applied to any dataset, irrespective of its distribution, post hoc. In contrast to other pixel-level uncertainty quantification methods, conformal prediction operates without requiring access to the underlying model and training dataset, concurrently offering statistically valid and informative prediction regions, all while maintaining computational efficiency. In response to the increased need to report uncertainty alongside point predictions, we bring attention to the promise of conformal prediction within the domain of Earth Observation (EO) applications. To accomplish this, we assess the current state of uncertainty quantification in the EO domain and found that only 20% of the reviewed Google Earth Engine (GEE) datasets incorporated a degree of uncertainty information, with unreliable methods prevalent. Next, we introduce modules that seamlessly integrate into existing GEE predictive modelling workflows and demonstrate the application of these tools for datasets spanning local to global scales, including the Dynamic World and Global Ecosystem Dynamics Investigation (GEDI) datasets. These case studies encompass regression and classification tasks, featuring both traditional and deep learning-based workflows. Subsequently, we discuss the opportunities arising from the use of conformal prediction in EO. We anticipate that the increased availability of easy-to-use implementations of conformal predictors, such as those provided here, will drive wider adoption of rigorous uncertainty quantification in EO, thereby enhancing the reliability of uses such as operational monitoring and decision making.
The frontier of quantum computing (QC) simulation on classical hardware is quickly reaching the hard scalability limits for computational feasibility. Nonetheless, there is still a need to simulate large quantum systems classically, as the Noisy Intermediate Scale Quantum (NISQ) devices are yet to be considered fault tolerant and performant enough in terms of operations per second. Each of the two main exact simulation techniques, state vector and tensor network simulators, boasts specific limitations. The exponential memory requirement of state vector simulation, when compared to the qubit register sizes of currently available quantum computers, quickly saturates the capacity of the top HPC machines currently available. Tensor network contraction approaches, which encode quantum circuits into tensor networks and then contract them over an output bit string to obtain its probability amplitude, still fall short of the inherent complexity of finding an optimal contraction path, which maps to a max-cut problem on a dense mesh, a notably NP-hard problem. This article aims at investigating the limits of current state-of-the-art simulation techniques on a test bench made of eight widely used quantum subroutines, each in 31 different configurations, with special emphasis on performance. We then correlate the performance measures of the simulators with the metrics that characterise the benchmark circuits, identifying the main reasons behind the observed performance trend. From our observations, given the structure of a quantum circuit and the number of qubits, we highlight how to select the best simulation strategy, obtaining a speedup of up to an order of magnitude.
Human behaviors, including scientific activities, are shaped by the hierarchical divisions of geography. As a result, researchers' mobility patterns vary across regions, influencing several aspects of the scientific community. These aspects encompass career trajectories, knowledge transfer, international collaborations, talent circulation, innovation diffusion, resource distribution, and policy development. However, our understanding of the relationship between the hierarchical regional scale and scientific movements is limited. This study aims to understand the subtle role of the geographical scales on scientists' mobility patterns across cities, countries, and continents. To this end, we analyzed 2.03 million scientists from 1960 to 2021, spanning institutions, cities, countries, and continents. We built a model based on hierarchical regions with different administrative levels and assessed the tendency for mobility from one region to another and the attractiveness of each region. Our findings reveal distinct nested hierarchies of regional scales and the dynamic of scientists' relocation patterns. This study sheds light on the complex dynamics of scientists' mobility and offers insights into how geographical scale and administrative divisions influence career decisions.