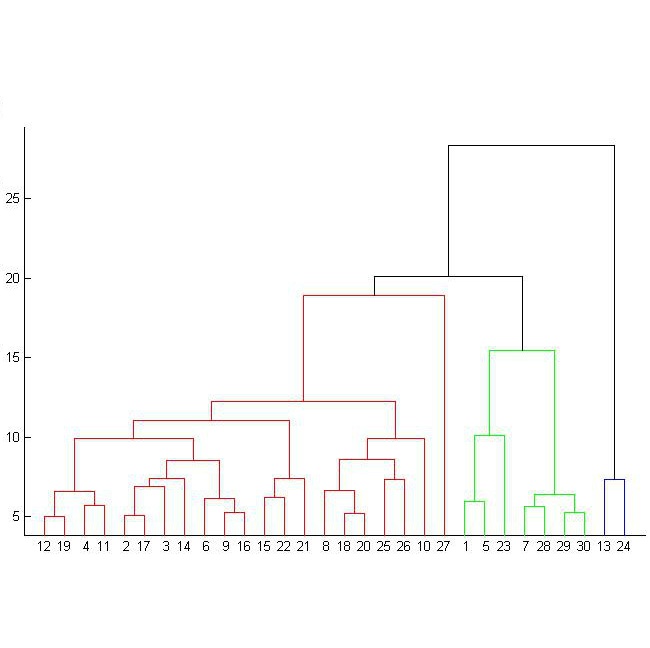
Agglomerative hierarchical clustering based on Ordered Weighted Averaging (OWA) operators not only generalises the single, complete, and average linkages, but also includes intercluster distances based on a few nearest or farthest neighbours, trimmed and winsorised means of pairwise point similarities, amongst many others. We explore the relationships between the famous Lance-Williams update formula and the extended OWA-based linkages with weights generated via infinite coefficient sequences. Furthermore, we provide some conditions for the weight generators to guarantee the resulting dendrograms to be free from unaesthetic inversions.
相關內容
Sample selection models represent a common methodology for correcting bias induced by data missing not at random. It is well known that these models are not empirically identifiable without exclusion restrictions. In other words, some variables predictive of missingness do not affect the outcome model of interest. The drive to establish this requirement often leads to the inclusion of irrelevant variables in the model. A recent proposal uses adaptive LASSO to circumvent this problem, but its performance depends on the so-called covariance assumption, which can be violated in small to moderate samples. Additionally, there are no tools yet for post-selection inference for this model. To address these challenges, we propose two families of spike-and-slab priors to conduct Bayesian variable selection in sample selection models. These prior structures allow for constructing a Gibbs sampler with tractable conditionals, which is scalable to the dimensions of practical interest. We illustrate the performance of the proposed methodology through a simulation study and present a comparison against adaptive LASSO and stepwise selection. We also provide two applications using publicly available real data. An implementation and code to reproduce the results in this paper can be found at //github.com/adam-iqbal/selection-spike-slab
Influenced mixed moving average fields are a versatile modeling class for spatio-temporal data. However, their predictive distribution is not generally known. Under this modeling assumption, we define a novel spatio-temporal embedding and a theory-guided machine learning approach that employs a generalized Bayesian algorithm to make ensemble forecasts. We employ Lipschitz predictors and determine fixed-time and any-time PAC Bayesian bounds in the batch learning setting. Performing causal forecast is a highlight of our methodology as its potential application to data with spatial and temporal short and long-range dependence. We then test the performance of our learning methodology by using linear predictors and data sets simulated from a spatio-temporal Ornstein-Uhlenbeck process.
Forecast combination involves using multiple forecasts to create a single, more accurate prediction. Recently, feature-based forecasting has been employed to either select the most appropriate forecasting models or to optimize the weights of their combination. In this paper, we present a multi-task optimization paradigm that focuses on solving both problems simultaneously and enriches current operational research approaches to forecasting. In essence, it incorporates an additional learning and optimization task into the standard feature-based forecasting approach, focusing on the identification of an optimal set of forecasting methods. During the training phase, an optimization model with linear constraints and quadratic objective function is employed to identify accurate and diverse methods for each time series. Moreover, within the training phase, a neural network is used to learn the behavior of that optimization model. Once training is completed the candidate set of methods is identified using the network. The proposed approach elicits the essential role of diversity in feature-based forecasting and highlights the interplay between model combination and model selection when optimizing forecasting ensembles. Experimental results on a large set of series from the M4 competition dataset show that our proposal enhances point forecast accuracy compared to state-of-the-art methods.
We consider the estimation of generalized additive models using basis expansions coupled with Bayesian model selection. Although Bayesian model selection is an intuitively appealing tool for regression splines, its use has traditionally been limited to Gaussian additive regression because of the availability of a tractable form of the marginal model likelihood. We extend the method to encompass the exponential family of distributions using the Laplace approximation to the likelihood. Although the approach exhibits success with any Gaussian-type prior distribution, there remains a lack of consensus regarding the best prior distribution for nonparametric regression through model selection. We observe that the classical unit information prior distribution for variable selection may not be well-suited for nonparametric regression using basis expansions. Instead, our investigation reveals that mixtures of g-priors are more suitable. We consider various mixtures of g-priors to evaluate the performance in estimating generalized additive models. Furthermore, we conduct a comparative analysis of several priors for knots to identify the most practically effective strategy. Our extensive simulation studies demonstrate the superiority of model selection-based approaches over other Bayesian methods.
This work studies the global convergence and implicit bias of Gauss Newton's (GN) when optimizing over-parameterized one-hidden layer networks in the mean-field regime. We first establish a global convergence result for GN in the continuous-time limit exhibiting a faster convergence rate compared to GD due to improved conditioning. We then perform an empirical study on a synthetic regression task to investigate the implicit bias of GN's method. While GN is consistently faster than GD in finding a global optimum, the learned model generalizes well on test data when starting from random initial weights with a small variance and using a small step size to slow down convergence. Specifically, our study shows that such a setting results in a hidden learning phenomenon, where the dynamics are able to recover features with good generalization properties despite the model having sub-optimal training and test performances due to an under-optimized linear layer. This study exhibits a trade-off between the convergence speed of GN and the generalization ability of the learned solution.
This work introduces UstanceBR, a multimodal corpus in the Brazilian Portuguese Twitter domain for target-based stance prediction. The corpus comprises 86.8 k labelled stances towards selected target topics, and extensive network information about the users who published these stances on social media. In this article we describe the corpus multimodal data, and a number of usage examples in both in-domain and zero-shot stance prediction based on text- and network-related information, which are intended to provide initial baseline results for future studies in the field.
We adopt the integral definition of the fractional Laplace operator and study an optimal control problem on Lipschitz domains that involves a fractional elliptic partial differential equation (PDE) as state equation and a control variable that enters the state equation as a coefficient; pointwise constraints on the control variable are considered as well. We establish the existence of optimal solutions and analyze first and, necessary and sufficient, second order optimality conditions. Regularity estimates for optimal variables are also analyzed. We develop two finite element discretization strategies: a semidiscrete scheme in which the control variable is not discretized, and a fully discrete scheme in which the control variable is discretized with piecewise constant functions. For both schemes, we analyze the convergence properties of discretizations and derive error estimates.
Normal modal logics extending the logic K4.3 of linear transitive frames are known to lack the Craig interpolation property, except some logics of bounded depth such as S5. We turn this `negative' fact into a research question and pursue a non-uniform approach to Craig interpolation by investigating the following interpolant existence problem: decide whether there exists a Craig interpolant between two given formulas in any fixed logic above K4.3. Using a bisimulation-based characterisation of interpolant existence for descriptive frames, we show that this problem is decidable and coNP-complete for all finitely axiomatisable normal modal logics containing K4.3. It is thus not harder than entailment in these logics, which is in sharp contrast to other recent non-uniform interpolation results. We also extend our approach to Priorean temporal logics (with both past and future modalities) over the standard time flows-the integers, rationals, reals, and finite strict linear orders-none of which is blessed with the Craig interpolation property.
With the rising concern on model interpretability, the application of eXplainable AI (XAI) tools on deepfake detection models has been a topic of interest recently. In image classification tasks, XAI tools highlight pixels influencing the decision given by a model. This helps in troubleshooting the model and determining areas that may require further tuning of parameters. With a wide range of tools available in the market, choosing the right tool for a model becomes necessary as each one may highlight different sets of pixels for a given image. There is a need to evaluate different tools and decide the best performing ones among them. Generic XAI evaluation methods like insertion or removal of salient pixels/segments are applicable for general image classification tasks but may produce less meaningful results when applied on deepfake detection models due to their functionality. In this paper, we perform experiments to show that generic removal/insertion XAI evaluation methods are not suitable for deepfake detection models. We also propose and implement an XAI evaluation approach specifically suited for deepfake detection models.
We give a recursive construction for projective Reed-Muller codes in terms of affine Reed-Muller codes and projective Reed-Muller codes in fewer variables. From this construction, we obtain the dimension of the subfield subcodes of projective Reed-Muller codes for some particular degrees that give codes with good parameters. Moreover, from this recursive construction we are able to derive a lower bound for the generalized Hamming weights of projective Reed-Muller codes which, together with the basic properties of the generalized Hamming weights, allows us to determine most of the weight hierarchy of projective Reed-Muller codes in many cases.