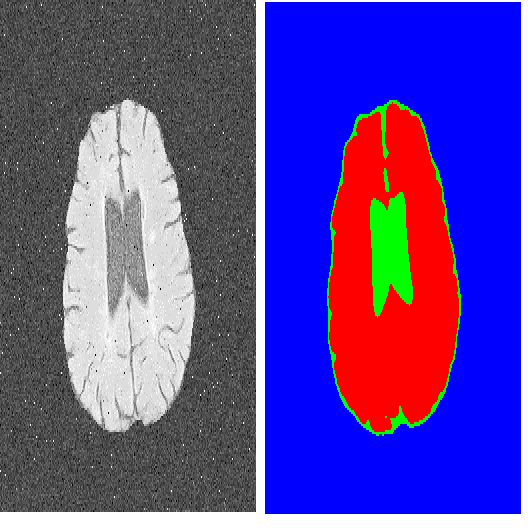
Medical segmentation models are evaluated empirically. As such an evaluation is based on a limited set of example images, it is unavoidably noisy. Beyond a mean performance measure, reporting confidence intervals is thus crucial. However, this is rarely done in medical image segmentation. The width of the confidence interval depends on the test set size and on the spread of the performance measure (its standard-deviation across of the test set). For classification, many test images are needed to avoid wide confidence intervals. Segmentation, however, has not been studied, and it differs by the amount of information brought by a given test image. In this paper, we study the typical confidence intervals in medical image segmentation. We carry experiments on 3D image segmentation using the standard nnU-net framework, two datasets from the Medical Decathlon challenge and two performance measures: the Dice accuracy and the Hausdorff distance. We show that the parametric confidence intervals are reasonable approximations of the bootstrap estimates for varying test set sizes and spread of the performance metric. Importantly, we show that the test size needed to achieve a given precision is often much lower than for classification tasks. Typically, a 1% wide confidence interval requires about 100-200 test samples when the spread is low (standard-deviation around 3%). More difficult segmentation tasks may lead to higher spreads and require over 1000 samples.
相關內容
Confounder selection, namely choosing a set of covariates to control for confounding between a treatment and an outcome, is arguably the most important step in the design of observational studies. Previous methods, such as Pearl's celebrated back-door criterion, typically require pre-specifying a causal graph, which can often be difficult in practice. We propose an interactive procedure for confounder selection that does not require pre-specifying the graph or the set of observed variables. This procedure iteratively expands the causal graph by finding what we call "primary adjustment sets" for a pair of possibly confounded variables. This can be viewed as inverting a sequence of latent projections of the underlying causal graph. Structural information in the form of primary adjustment sets is elicited from the user, bit by bit, until either a set of covariates are found to control for confounding or it can be determined that no such set exists. We show that if the user correctly specifies the primary adjustment sets in every step, our procedure is both sound and complete.
This article presents a new tool for the automatic detection of meteors. Fast Meteor Detection Toolbox (FMDT) is able to detect meteor sightings by analyzing videos acquired by cameras onboard weather balloons or within airplane with stabilization. The challenge consists in designing a processing chain composed of simple algorithms, that are robust to the high fluctuation of the videos and that satisfy the constraints on power consumption (10 W) and real-time processing (25 frames per second).
With the increasing availability of large scale datasets, computational power and tools like automatic differentiation and expressive neural network architectures, sequential data are now often treated in a data-driven way, with a dynamical model trained from the observation data. While neural networks are often seen as uninterpretable black-box architectures, they can still benefit from physical priors on the data and from mathematical knowledge. In this paper, we use a neural network architecture which leverages the long-known Koopman operator theory to embed dynamical systems in latent spaces where their dynamics can be described linearly, enabling a number of appealing features. We introduce methods that enable to train such a model for long-term continuous reconstruction, even in difficult contexts where the data comes in irregularly-sampled time series. The potential for self-supervised learning is also demonstrated, as we show the promising use of trained dynamical models as priors for variational data assimilation techniques, with applications to e.g. time series interpolation and forecasting.
Brain segmentation from neonatal MRI images is a very challenging task due to large changes in the shape of cerebral structures and variations in signal intensities reflecting the gestational process. In this context, there is a clear need for segmentation techniques that are robust to variations in image contrast and to the spatial configuration of anatomical structures. In this work, we evaluate the potential of synthetic learning, a contrast-independent model trained using synthetic images generated from the ground truth labels of very few subjects.We base our experiments on the dataset released by the developmental Human Connectome Project, for which high-quality T1- and T2-weighted images are available for more than 700 babies aged between 26 and 45 weeks post-conception. First, we confirm the impressive performance of a standard Unet trained on a few T2-weighted volumes, but also confirm that such models learn intensity-related features specific to the training domain. We then evaluate the synthetic learning approach and confirm its robustness to variations in image contrast by reporting the capacity of such a model to segment both T1- and T2-weighted images from the same individuals. However, we observe a clear influence of the age of the baby on the predictions. We improve the performance of this model by enriching the synthetic training set with realistic motion artifacts and over-segmentation of the white matter. Based on extensive visual assessment, we argue that the better performance of the model trained on real T2w data may be due to systematic errors in the ground truth. We propose an original experiment combining two definitions of the ground truth allowing us to show that learning from real data will reproduce any systematic bias from the training set, while synthetic models can avoid this limitation. Overall, our experiments confirm that synthetic learning is an effective solution for segmenting neonatal brain MRI. Our adapted synthetic learning approach combines key features that will be instrumental for large multi-site studies and clinical applications.
The (modern) arbitrary derivative (ADER) approach is a popular technique for the numerical solution of differential problems based on iteratively solving an implicit discretization of their weak formulation. In this work, focusing on an ODE context, we investigate several strategies to improve this approach. Our initial emphasis is on the order of accuracy of the method in connection with the polynomial discretization of the weak formulation. We demonstrate that precise choices lead to higher-order convergences in comparison to the existing literature. Then, we put ADER methods into a Deferred Correction (DeC) formalism. This allows to determine the optimal number of iterations, which is equal to the formal order of accuracy of the method, and to introduce efficient $p$-adaptive modifications. These are defined by matching the order of accuracy achieved and the degree of the polynomial reconstruction at each iteration. We provide analytical and numerical results, including the stability analysis of the new modified methods, the investigation of the computational efficiency, an application to adaptivity and an application to hyperbolic PDEs with a Spectral Difference (SD) space discretization.
In this work, we discuss some properties of the eigenvalues of some classes of signed complete graphs. We also obtain the form of characteristic polynomial for these graphs.
As we are aware, various types of methods have been proposed to approximate the Caputo fractional derivative numerically. A common challenge of the methods is the non-local property of the Caputo fractional derivative which leads to the slow and memory consuming methods. Diffusive representation of fractional derivative is an efficient tool to overcome the mentioned challenge. This paper presents two new diffusive representations to approximate the Caputo fractional derivative of order $0<\alpha<1$. Error analysis of the newly presented methods together with some numerical examples are provided at the end.
We present ResMLP, an architecture built entirely upon multi-layer perceptrons for image classification. It is a simple residual network that alternates (i) a linear layer in which image patches interact, independently and identically across channels, and (ii) a two-layer feed-forward network in which channels interact independently per patch. When trained with a modern training strategy using heavy data-augmentation and optionally distillation, it attains surprisingly good accuracy/complexity trade-offs on ImageNet. We will share our code based on the Timm library and pre-trained models.
A key requirement for the success of supervised deep learning is a large labeled dataset - a condition that is difficult to meet in medical image analysis. Self-supervised learning (SSL) can help in this regard by providing a strategy to pre-train a neural network with unlabeled data, followed by fine-tuning for a downstream task with limited annotations. Contrastive learning, a particular variant of SSL, is a powerful technique for learning image-level representations. In this work, we propose strategies for extending the contrastive learning framework for segmentation of volumetric medical images in the semi-supervised setting with limited annotations, by leveraging domain-specific and problem-specific cues. Specifically, we propose (1) novel contrasting strategies that leverage structural similarity across volumetric medical images (domain-specific cue) and (2) a local version of the contrastive loss to learn distinctive representations of local regions that are useful for per-pixel segmentation (problem-specific cue). We carry out an extensive evaluation on three Magnetic Resonance Imaging (MRI) datasets. In the limited annotation setting, the proposed method yields substantial improvements compared to other self-supervision and semi-supervised learning techniques. When combined with a simple data augmentation technique, the proposed method reaches within 8% of benchmark performance using only two labeled MRI volumes for training, corresponding to only 4% (for ACDC) of the training data used to train the benchmark.

Recent advances in 3D fully convolutional networks (FCN) have made it feasible to produce dense voxel-wise predictions of volumetric images. In this work, we show that a multi-class 3D FCN trained on manually labeled CT scans of several anatomical structures (ranging from the large organs to thin vessels) can achieve competitive segmentation results, while avoiding the need for handcrafting features or training class-specific models. To this end, we propose a two-stage, coarse-to-fine approach that will first use a 3D FCN to roughly define a candidate region, which will then be used as input to a second 3D FCN. This reduces the number of voxels the second FCN has to classify to ~10% and allows it to focus on more detailed segmentation of the organs and vessels. We utilize training and validation sets consisting of 331 clinical CT images and test our models on a completely unseen data collection acquired at a different hospital that includes 150 CT scans, targeting three anatomical organs (liver, spleen, and pancreas). In challenging organs such as the pancreas, our cascaded approach improves the mean Dice score from 68.5 to 82.2%, achieving the highest reported average score on this dataset. We compare with a 2D FCN method on a separate dataset of 240 CT scans with 18 classes and achieve a significantly higher performance in small organs and vessels. Furthermore, we explore fine-tuning our models to different datasets. Our experiments illustrate the promise and robustness of current 3D FCN based semantic segmentation of medical images, achieving state-of-the-art results. Our code and trained models are available for download: //github.com/holgerroth/3Dunet_abdomen_cascade.