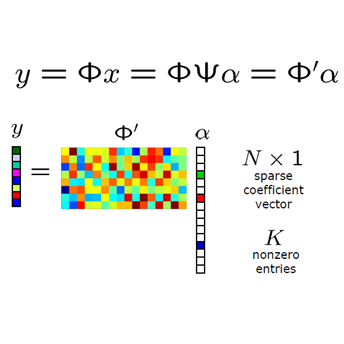
Noiseless compressive sensing is a protocol that enables undersampling and later recovery of a signal without loss of information. This compression is possible because the signal is usually sufficiently sparse in a given basis. Currently, the algorithm offering the best tradeoff between compression rate, robustness, and speed for compressive sensing is the LASSO (l1-norm bias) algorithm. However, many studies have pointed out the possibility that the implementation of lp-norms biases, with p smaller than one, could give better performance while sacrificing convexity. In this work, we focus specifically on the extreme case of the l0-based reconstruction, a task that is complicated by the discontinuity of the loss. In the first part of the paper, we describe via statistical physics methods, and in particular the replica method, how the solutions to this optimization problem are arranged in a clustered structure. We observe two distinct regimes: one at low compression rate where the signal can be recovered exactly, and one at high compression rate where the signal cannot be recovered accurately. In the second part, we present two message-passing algorithms based on our first results for the l0-norm optimization problem. The proposed algorithms are able to recover the signal at compression rates higher than the ones achieved by LASSO while being computationally efficient.
相關內容
Spectral clustering is a well-known technique which identifies $k$ clusters in an undirected graph with weight matrix $W\in\mathbb{R}^{n\times n}$ by exploiting its graph Laplacian $L(W)$, whose eigenvalues $0=\lambda_1\leq \lambda_2 \leq \dots \leq \lambda_n$ and eigenvectors are related to the $k$ clusters. Since the computation of $\lambda_{k+1}$ and $\lambda_k$ affects the reliability of this method, the $k$-th spectral gap $\lambda_{k+1}-\lambda_k$ is often considered as a stability indicator. This difference can be seen as an unstructured distance between $L(W)$ and an arbitrary symmetric matrix $L_\star$ with vanishing $k$-th spectral gap. A more appropriate structured distance to ambiguity such that $L_\star$ represents the Laplacian of a graph has been proposed by Andreotti et al. (2021). Slightly differently, we consider the objective functional $ F(\Delta)=\lambda_{k+1}\left(L(W+\Delta)\right)-\lambda_k\left(L(W+\Delta)\right)$, where $\Delta$ is a perturbation such that $W+\Delta$ has non-negative entries and the same pattern of $W$. We look for an admissible perturbation $\Delta_\star$ of smallest Frobenius norm such that $F(\Delta_\star)=0$. In order to solve this optimization problem, we exploit its low rank underlying structure. We formulate a rank-4 symmetric matrix ODE whose stationary points are the optimizers sought. The integration of this equation benefits from the low rank structure with a moderate computational effort and memory requirement, as it is shown in some illustrative numerical examples.
A parametric class of trust-region algorithms for unconstrained nonconvex optimization is considered where the value of the objective function is never computed. The class contains a deterministic version of the first-order Adagrad method typically used for minimization of noisy function, but also allows the use of (possibly approximate) second-order information when available. The rate of convergence of methods in the class is analyzed and is shown to be identical to that known for first-order optimization methods using both function and gradients values, recovering existing results for purely-first order variants and improving the explicit dependence on problem dimension. This rate is shown to be essentially sharp. A new class of methods is also presented, for which a slightly worse and essentially sharp complexity result holds. Limited numerical experiments show that the new methods' performance may be comparable to that of standard steepest descent, despite using significantly less information, and that this performance is relatively insensitive to noise.
The numerical evaluation of statistics plays a crucial role in statistical physics and its applied fields. It is possible to evaluate the statistics for a stochastic differential equation with Gaussian white noise via the corresponding backward Kolmogorov equation. The important notice is that there is no need to obtain the solution of the backward Kolmogorov equation on the whole domain; it is enough to evaluate a value of the solution at a certain point that corresponds to the initial coordinate for the stochastic differential equation. For this aim, an algorithm based on combinatorics has recently been developed. In this paper, we discuss a higher-order approximation of resolvent, and an algorithm based on a second-order approximation is proposed. The proposed algorithm shows a second-order convergence. Furthermore, the convergence property of the naive algorithms naturally leads to extrapolation methods; they work well to calculate a more accurate value with fewer computational costs. The proposed method is demonstrated with the Ornstein-Uhlenbeck process and the noisy van der Pol system.
We introduce the mean inverse integrator (MII), a novel approach to increase the accuracy when training neural networks to approximate vector fields of dynamical systems from noisy data. This method can be used to average multiple trajectories obtained by numerical integrators such as Runge-Kutta methods. We show that the class of mono-implicit Runge-Kutta methods (MIRK) has particular advantages when used in connection with MII. When training vector field approximations, explicit expressions for the loss functions are obtained when inserting the training data in the MIRK formulae, unlocking symmetric and high-order integrators that would otherwise be implicit for initial value problems. The combined approach of applying MIRK within MII yields a significantly lower error compared to the plain use of the numerical integrator without averaging the trajectories. This is demonstrated with experiments using data from several (chaotic) Hamiltonian systems. Additionally, we perform a sensitivity analysis of the loss functions under normally distributed perturbations, supporting the favorable performance of MII.
This paper is concerned with function reconstruction from samples. The sampling points used in several approaches are (1) structured points connected with fast algorithms or (2) unstructured points coming from, e.g., an initial random draw to achieve an improved information complexity. We connect both approaches and propose a subsampling of structured points in an offline step. In particular, we start with structured quadrature points (QMC), which provide stable $L_2$ reconstruction properties. The subsampling procedure consists of a computationally inexpensive random step followed by a deterministic procedure to further reduce the number of points while keeping its information. In these points functions (belonging to a RKHS of bounded functions) will be sampled and reconstructed from whilst achieving state of the art error decay. Our method is dimension-independent and is applicable as soon as we know some initial quadrature points. We apply our general findings on the $d$-dimensional torus to subsample rank-1 lattices, where it is known that full rank-1 lattices lose half the optimal order of convergence (expressed in terms of the size of the lattice). In contrast to that, our subsampled version regains the optimal rate since many of the lattice points are not needed. Moreover, we utilize fast and memory efficient Fourier algorithms in order to compute the approximation. Numerical experiments in several dimensions support our findings.
Predictive dynamical models for marine ecosystems are used for a variety of needs. Due to sparse measurements and limited understanding of the myriad of ocean processes, there is however significant uncertainty. There is model uncertainty in the parameter values, functional forms with diverse parameterizations, level of complexity needed, and thus in the state fields. We develop a Bayesian model learning methodology that allows interpolation in the space of candidate models and discovery of new models from noisy, sparse, and indirect observations, all while estimating state fields and parameter values, as well as the joint PDFs of all learned quantities. We address the challenges of high-dimensional and multidisciplinary dynamics governed by PDEs by using state augmentation and the computationally efficient GMM-DO filter. Our innovations include stochastic formulation and complexity parameters to unify candidate models into a single general model as well as stochastic expansion parameters within piecewise function approximations to generate dense candidate model spaces. These innovations allow handling many compatible and embedded candidate models, possibly none of which are accurate, and learning elusive unknown functional forms. Our new methodology is generalizable, interpretable, and extrapolates out of the space of models to discover new ones. We perform a series of twin experiments based on flows past a ridge coupled with three-to-five component ecosystem models, including flows with chaotic advection. The probabilities of known, uncertain, and unknown model formulations, and of state fields and parameters, are updated jointly using Bayes' law. Non-Gaussian statistics, ambiguity, and biases are captured. The parameter values and model formulations that best explain the data are identified. When observations are sufficiently informative, model complexity and functions are discovered.
In this article we develop a high order accurate method to solve the incompressible boundary layer equations in a provably stable manner.~We first derive continuous energy estimates,~and then proceed to the discrete setting.~We formulate the discrete approximation using high-order finite difference methods on summation-by-parts form and implement the boundary conditions weakly using the simultaneous approximation term method.~By applying the discrete energy method and imitating the continuous analysis,~the discrete estimate that resembles the continuous counterpart is obtained proving stability.~We also show that these newly derived boundary conditions removes the singularities associated with the null-space of the nonlinear discrete spatial operator.~Numerical experiments that verifies the high-order accuracy of the scheme and coincides with the theoretical results are presented.~The numerical results are compared with the well-known Blasius similarity solution as well as that resulting from the solution of the incompressible Navier Stokes equations.
The aim of this study is to determine the perceived stress levels of 150 individuals and analyze the responses given to adapted questions in Turkish using machine learning. The test consists of 14 questions, each scored on a scale of 0 to 4, resulting in a total score range of 0-56. Out of these questions, 7 are formulated in a negative context and scored accordingly, while the remaining 7 are formulated in a positive context and scored in reverse. The test is also designed to identify two sub-factors: perceived self-efficacy and stress/discomfort perception. The main objectives of this research are to demonstrate that test questions may not have equal importance using artificial intelligence techniques, reveal which questions exhibit variations in the society using machine learning, and ultimately demonstrate the existence of distinct patterns observed psychologically. This study provides a different perspective from the existing psychology literature by repeating the test through machine learning. Additionally, it questions the accuracy of the scale used to interpret the results of the perceived stress test and emphasizes the importance of considering differences in the prioritization of test questions. The findings of this study offer new insights into coping strategies and therapeutic approaches in dealing with stress. Source code: //github.com/toygarr/ppl-r-stressed
In this paper, we initiate the study of local model reconstruction attacks for federated learning, where a honest-but-curious adversary eavesdrops the messages exchanged between a targeted client and the server, and then reconstructs the local/personalized model of the victim. The local model reconstruction attack allows the adversary to trigger other classical attacks in a more effective way, since the local model only depends on the client's data and can leak more private information than the global model learned by the server. Additionally, we propose a novel model-based attribute inference attack in federated learning leveraging the local model reconstruction attack. We provide an analytical lower-bound for this attribute inference attack. Empirical results using real world datasets confirm that our local reconstruction attack works well for both regression and classification tasks. Moreover, we benchmark our novel attribute inference attack against the state-of-the-art attacks in federated learning. Our attack results in higher reconstruction accuracy especially when the clients' datasets are heterogeneous. Our work provides a new angle for designing powerful and explainable attacks to effectively quantify the privacy risk in FL.
This paper is concerned with the lossy compression of general random variables, specifically with rate-distortion theory and quantization of random variables taking values in general measurable spaces such as, e.g., manifolds and fractal sets. Manifold structures are prevalent in data science, e.g., in compressed sensing, machine learning, image processing, and handwritten digit recognition. Fractal sets find application in image compression and in the modeling of Ethernet traffic. Our main contributions are bounds on the rate-distortion function and the quantization error. These bounds are very general and essentially only require the existence of reference measures satisfying certain regularity conditions in terms of small ball probabilities. To illustrate the wide applicability of our results, we particularize them to random variables taking values in i) manifolds, namely, hyperspheres and Grassmannians, and ii) self-similar sets characterized by iterated function systems satisfying the weak separation property.