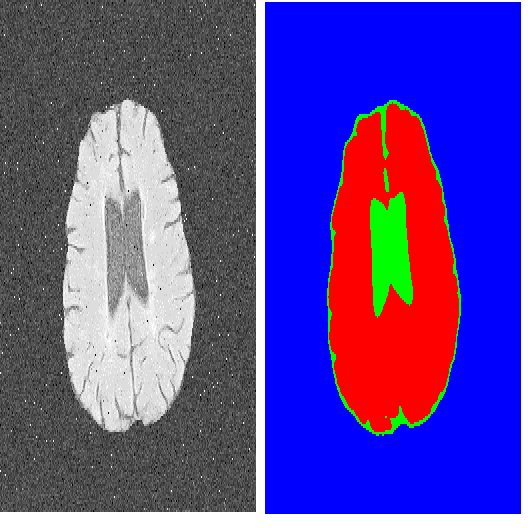
Out of distribution (OOD) medical images are frequently encountered, e.g. because of site- or scanner differences, or image corruption. OOD images come with a risk of incorrect image segmentation, potentially negatively affecting downstream diagnoses or treatment. To ensure robustness to such incorrect segmentations, we propose Laplacian Segmentation Networks (LSN) that jointly model epistemic (model) and aleatoric (data) uncertainty in image segmentation. We capture data uncertainty with a spatially correlated logit distribution. For model uncertainty, we propose the first Laplace approximation of the weight posterior that scales to large neural networks with skip connections that have high-dimensional outputs. Empirically, we demonstrate that modelling spatial pixel correlation allows the Laplacian Segmentation Network to successfully assign high epistemic uncertainty to out-of-distribution objects appearing within images.
相關內容
Supervised masking approaches in the time-frequency domain aim to employ deep neural networks to estimate a multiplicative mask to extract clean speech. This leads to a single estimate for each input without any guarantees or measures of reliability. In this paper, we study the benefits of modeling uncertainty in clean speech estimation. Prediction uncertainty is typically categorized into aleatoric uncertainty and epistemic uncertainty. The former refers to inherent randomness in data, while the latter describes uncertainty in the model parameters. In this work, we propose a framework to jointly model aleatoric and epistemic uncertainties in neural network-based speech enhancement. The proposed approach captures aleatoric uncertainty by estimating the statistical moments of the speech posterior distribution and explicitly incorporates the uncertainty estimate to further improve clean speech estimation. For epistemic uncertainty, we investigate two Bayesian deep learning approaches: Monte Carlo dropout and Deep ensembles to quantify the uncertainty of the neural network parameters. Our analyses show that the proposed framework promotes capturing practical and reliable uncertainty, while combining different sources of uncertainties yields more reliable predictive uncertainty estimates. Furthermore, we demonstrate the benefits of modeling uncertainty on speech enhancement performance by evaluating the framework on different datasets, exhibiting notable improvement over comparable models that fail to account for uncertainty.

Single-channel deep speech enhancement approaches often estimate a single multiplicative mask to extract clean speech without a measure of its accuracy. Instead, in this work, we propose to quantify the uncertainty associated with clean speech estimates in neural network-based speech enhancement. Predictive uncertainty is typically categorized into aleatoric uncertainty and epistemic uncertainty. The former accounts for the inherent uncertainty in data and the latter corresponds to the model uncertainty. Aiming for robust clean speech estimation and efficient predictive uncertainty quantification, we propose to integrate statistical complex Gaussian mixture models (CGMMs) into a deep speech enhancement framework. More specifically, we model the dependency between input and output stochastically by means of a conditional probability density and train a neural network to map the noisy input to the full posterior distribution of clean speech, modeled as a mixture of multiple complex Gaussian components. Experimental results on different datasets show that the proposed algorithm effectively captures predictive uncertainty and that combining powerful statistical models and deep learning also delivers a superior speech enhancement performance.
We propose gradient-enhanced PINNs based on transfer learning (TL-gPINNs) for inverse problems of the function coefficient discovery in order to overcome deficiency of the discrete characterization of the PDE loss in neural networks and improve accuracy of function feature description, which offers a new angle of view for gPINNs. The TL-gPINN algorithm is applied to infer the unknown variable coefficients of various forms (the polynomial, trigonometric function, hyperbolic function and fractional polynomial) and multiple variable coefficients simultaneously with abundant soliton solutions for the well-known variable coefficient nonlinear Schr\"{o}odinger equation. Compared with the PINN and gPINN, TL-gPINN yields considerable improvement in accuracy. Moreover, our method leverages the advantage of the transfer learning technique, which can help to mitigate the problem of inefficiency caused by extra loss terms of the gradient. Numerical results fully demonstrate the effectiveness of the TL-gPINN method in significant accuracy enhancement, and it also outperforms gPINN in efficiency even when the training data was corrupted with different levels of noise or hyper-parameters of neural networks are arbitrarily changed.
The use of deep learning approaches for image reconstruction is of contemporary interest in radiology, especially for approaches that solve inverse problems associated with imaging. In deployment, these models may be exposed to input distributions that are widely shifted from training data, due in part to data biases or drifts. We propose a metric based on local Lipschitz determined from a single trained model that can be used to estimate the model uncertainty for image reconstructions. We demonstrate a monotonic relationship between the local Lipschitz value and Mean Absolute Error and show that this method can be used to provide a threshold that determines whether a given DL reconstruction approach was well suited to the task. Our uncertainty estimation method can be used to identify out-of-distribution test samples, relate information regarding epistemic uncertainties, and guide proper data augmentation. Quantifying uncertainty of learned reconstruction approaches is especially pertinent to the medical domain where reconstructed images must remain diagnostically accurate.
A Bayesian treatment of deep learning allows for the computation of uncertainties associated with the predictions of deep neural networks. We show how the concept of Errors-in-Variables can be used in Bayesian deep regression to also account for the uncertainty associated with the input of the employed neural network. The presented approach thereby exploits a relevant, but generally overlooked, source of uncertainty and yields a decomposition of the predictive uncertainty into an aleatoric and epistemic part that is more complete and, in many cases, more consistent from a statistical perspective. We discuss the approach along various simulated and real examples and observe that using an Errors-in-Variables model leads to an increase in the uncertainty while preserving the prediction performance of models without Errors-in-Variables. For examples with known regression function we observe that this ground truth is substantially better covered by the Errors-in-Variables model, indicating that the presented approach leads to a more reliable uncertainty estimation.
It is well known that semantic segmentation neural networks (SSNNs) produce dense segmentation maps to resolve the objects' boundaries while restrict the prediction on down-sampled grids to alleviate the computational cost. A striking balance between the accuracy and the training cost of the SSNNs such as U-Net exists. We propose a spectral analysis to investigate the correlations among the resolution of the down sampled grid, the loss function and the accuracy of the SSNNs. By analyzing the network back-propagation process in frequency domain, we discover that the traditional loss function, cross-entropy, and the key features of CNN are mainly affected by the low-frequency components of segmentation labels. Our discoveries can be applied to SSNNs in several ways including (i) determining an efficient low resolution grid for resolving the segmentation maps (ii) pruning the networks by truncating the high frequency decoder features for saving computation costs, and (iii) using block-wise weak annotation for saving the labeling time. Experimental results shown in this paper agree with our spectral analysis for the networks such as DeepLab V3+ and Deep Aggregation Net (DAN).
We present an approach for safe motion planning under robot state and environment (obstacle and landmark location) uncertainties. To this end, we first develop an approach that accounts for the landmark uncertainties during robot localization. Existing planning approaches assume that the landmark locations are well known or are known with little uncertainty. However, this might not be true in practice. Noisy sensors and imperfect motions compound to the errors originating from the estimate of environment features. Moreover, possible occlusions and dynamic objects in the environment render imperfect landmark estimation. Consequently, not considering this uncertainty can wrongly localize the robot, leading to inefficient plans. Our approach thus incorporates the landmark uncertainty within the Bayes filter estimation framework. We also analyze the effect of considering this uncertainty and delineate the conditions under which it can be ignored. Second, we extend the state-of-the-art by computing an exact expression for the collision probability under Gaussian distributed robot motion, perception and obstacle location uncertainties. We formulate the collision probability process as a quadratic form in random variables. Under Gaussian distribution assumptions, an exact expression for collision probability is thus obtained which is computable in real-time. In contrast, existing approaches approximate the collision probability using upper-bounds that can lead to overly conservative estimate and thereby suboptimal plans. We demonstrate and evaluate our approach using a theoretical example and simulations. We also present a comparison of our approach to different state-of-the-art methods.
Graph Neural Networks (GNNs) draw their strength from explicitly modeling the topological information of structured data. However, existing GNNs suffer from limited capability in capturing the hierarchical graph representation which plays an important role in graph classification. In this paper, we innovatively propose hierarchical graph capsule network (HGCN) that can jointly learn node embeddings and extract graph hierarchies. Specifically, disentangled graph capsules are established by identifying heterogeneous factors underlying each node, such that their instantiation parameters represent different properties of the same entity. To learn the hierarchical representation, HGCN characterizes the part-whole relationship between lower-level capsules (part) and higher-level capsules (whole) by explicitly considering the structure information among the parts. Experimental studies demonstrate the effectiveness of HGCN and the contribution of each component.
Incompleteness is a common problem for existing knowledge graphs (KGs), and the completion of KG which aims to predict links between entities is challenging. Most existing KG completion methods only consider the direct relation between nodes and ignore the relation paths which contain useful information for link prediction. Recently, a few methods take relation paths into consideration but pay less attention to the order of relations in paths which is important for reasoning. In addition, these path-based models always ignore nonlinear contributions of path features for link prediction. To solve these problems, we propose a novel KG completion method named OPTransE. Instead of embedding both entities of a relation into the same latent space as in previous methods, we project the head entity and the tail entity of each relation into different spaces to guarantee the order of relations in the path. Meanwhile, we adopt a pooling strategy to extract nonlinear and complex features of different paths to further improve the performance of link prediction. Experimental results on two benchmark datasets show that the proposed model OPTransE performs better than state-of-the-art methods.
Embedding models for deterministic Knowledge Graphs (KG) have been extensively studied, with the purpose of capturing latent semantic relations between entities and incorporating the structured knowledge into machine learning. However, there are many KGs that model uncertain knowledge, which typically model the inherent uncertainty of relations facts with a confidence score, and embedding such uncertain knowledge represents an unresolved challenge. The capturing of uncertain knowledge will benefit many knowledge-driven applications such as question answering and semantic search by providing more natural characterization of the knowledge. In this paper, we propose a novel uncertain KG embedding model UKGE, which aims to preserve both structural and uncertainty information of relation facts in the embedding space. Unlike previous models that characterize relation facts with binary classification techniques, UKGE learns embeddings according to the confidence scores of uncertain relation facts. To further enhance the precision of UKGE, we also introduce probabilistic soft logic to infer confidence scores for unseen relation facts during training. We propose and evaluate two variants of UKGE based on different learning objectives. Experiments are conducted on three real-world uncertain KGs via three tasks, i.e. confidence prediction, relation fact ranking, and relation fact classification. UKGE shows effectiveness in capturing uncertain knowledge by achieving promising results on these tasks, and consistently outperforms baselines on these tasks.