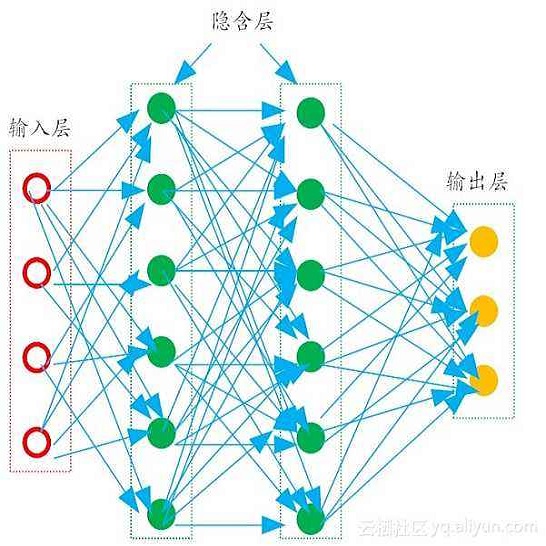
Algebraic Multigrid (AMG) is one of the most used iterative algorithms for solving large sparse linear equations $Ax=b$. In AMG, the coarse grid is a key component that affects the efficiency of the algorithm, the construction of which relies on the strong threshold parameter $\theta$. This parameter is generally chosen empirically, with a default value in many current AMG solvers of 0.25 for 2D problems and 0.5 for 3D problems. However, for many practical problems, the quality of the coarse grid and the efficiency of the AMG algorithm are sensitive to $\theta$; the default value is rarely optimal, and sometimes is far from it. Therefore, how to choose a better $\theta$ is an important question. In this paper, we propose a deep learning based auto-tuning method, AutoAMG($\theta$) for multiscale sparse linear equations, which are widely used in practical problems. The method uses Graph Neural Networks (GNNs) to extract matrix features, and a Multilayer Perceptron (MLP) to build the mapping between matrix features and the optimal $\theta$, which can adaptively output $\theta$ values for different matrices. Numerical experiments show that AutoAMG($\theta$) can achieve significant speedup compared to the default $\theta$ value.
相關內容
Based on the theory of homogeneous spaces we derive \textit{geometrically optimal edge attributes} to be used within the flexible message passing framework. We formalize the notion of weight sharing in convolutional networks as the sharing of message functions over point-pairs that should be treated equally. We define equivalence classes of point-pairs that are identical up to a transformation in the group and derive attributes that uniquely identify these classes. Weight sharing is then obtained by conditioning message functions on these attributes. As an application of the theory, we develop an efficient equivariant group convolutional network for processing 3D point clouds. The theory of homogeneous spaces tells us how to do group convolutions with feature maps over the homogeneous space of positions $\mathbb{R}^3$, position and orientations $\mathbb{R}^3 {\times} S^2$, and the group SE$(3)$ itself. Among these, $\mathbb{R}^3 {\times} S^2$ is an optimal choice due to the ability to represent directional information, which $\mathbb{R}^3$ methods cannot, and it significantly enhances computational efficiency compared to indexing features on the full SE$(3)$ group. We empirically support this claim by reaching state-of-the-art results -- in accuracy and speed -- on three different benchmarks: interatomic potential energy prediction, trajectory forecasting in N-body systems, and generating molecules via equivariant diffusion models.
Large Language Models (LLMs) have the ability to solve a variety of tasks, such as text summarization and mathematical questions, just out of the box, but they are often trained with a single task in mind. Due to high computational costs, the current trend is to use prompt instruction tuning to better adjust monolithic, pretrained LLMs for new -- but often individual -- downstream tasks. Thus, how one would expand prompt tuning to handle -- concomitantly -- heterogeneous tasks and data distributions is a widely open question. To address this gap, we suggest the use of \emph{Mixture of Prompts}, or MoPs, associated with smart gating functionality: the latter -- whose design is one of the contributions of this paper -- can identify relevant skills embedded in different groups of prompts and dynamically assign combined experts (i.e., collection of prompts), based on the target task. Additionally, MoPs are empirically agnostic to any model compression technique applied -- for efficiency reasons -- as well as instruction data source and task composition. In practice, MoPs can simultaneously mitigate prompt training "interference" in multi-task, multi-source scenarios (e.g., task and data heterogeneity across sources), as well as possible implications from model approximations. As a highlight, MoPs manage to decrease final perplexity from $\sim20\%$ up to $\sim70\%$, as compared to baselines, in the federated scenario, and from $\sim 3\%$ up to $\sim30\%$ in the centralized scenario.

Simultaneous localization and mapping (SLAM) is critical to the implementation of autonomous driving. Most LiDAR-inertial SLAM algorithms assume a static environment, leading to unreliable localization in dynamic environments. Moreover, the accurate tracking of moving objects is of great significance for the control and planning of autonomous vehicles. This study proposes LIMOT, a tightly-coupled multi-object tracking and LiDAR-inertial odometry system that is capable of accurately estimating the poses of both ego-vehicle and objects. We propose a trajectory-based dynamic feature filtering method, which filters out features belonging to moving objects by leveraging tracking results before scan-matching. Factor graph-based optimization is then conducted to optimize the bias of the IMU and the poses of both the ego-vehicle and surrounding objects in a sliding window. Experiments conducted on the KITTI tracking dataset and self-collected dataset show that our method achieves better pose and tracking accuracy than our previous work DL-SLOT and other baseline methods. Our open-source implementation is available at //github.com/tiev-tongji/LIMOT.
Solving a linear system $Ax=b$ is a fundamental scientific computing primitive for which numerous solvers and preconditioners have been developed. These come with parameters whose optimal values depend on the system being solved and are often impossible or too expensive to identify; thus in practice sub-optimal heuristics are used. We consider the common setting in which many related linear systems need to be solved, e.g. during a single numerical simulation. In this scenario, can we sequentially choose parameters that attain a near-optimal overall number of iterations, without extra matrix computations? We answer in the affirmative for Successive Over-Relaxation (SOR), a standard solver whose parameter $\omega$ has a strong impact on its runtime. For this method, we prove that a bandit online learning algorithm -- using only the number of iterations as feedback -- can select parameters for a sequence of instances such that the overall cost approaches that of the best fixed $\omega$ as the sequence length increases. Furthermore, when given additional structural information, we show that a contextual bandit method asymptotically achieves the performance of the instance-optimal policy, which selects the best $\omega$ for each instance. Our work provides the first learning-theoretic treatment of high-precision linear system solvers and the first end-to-end guarantees for data-driven scientific computing, demonstrating theoretically the potential to speed up numerical methods using well-understood learning algorithms.
Large Language Models (LLMs) have shown promise in the autonomous driving sector, particularly in generalization and interpretability. We introduce a unique object-level multimodal LLM architecture that merges vectorized numeric modalities with a pre-trained LLM to improve context understanding in driving situations. We also present a new dataset of 160k QA pairs derived from 10k driving scenarios, paired with high quality control commands collected with RL agent and question answer pairs generated by teacher LLM (GPT-3.5). A distinct pretraining strategy is devised to align numeric vector modalities with static LLM representations using vector captioning language data. We also introduce an evaluation metric for Driving QA and demonstrate our LLM-driver's proficiency in interpreting driving scenarios, answering questions, and decision-making. Our findings highlight the potential of LLM-based driving action generation in comparison to traditional behavioral cloning. We make our benchmark, datasets, and model available for further exploration.
We introduce an iterative solver named MINARES for symmetric linear systems $Ax \approx b$, where $A$ is possibly singular. MINARES is based on the symmetric Lanczos process, like MINRES and MINRES-QLP, but it minimizes $\|Ar_k\|$ in each Krylov subspace rather than $\|r_k\|$, where $r_k$ is the current residual vector. When $A$ is symmetric, MINARES minimizes the same quantity $\|Ar_k\|$ as LSMR, but in more relevant Krylov subspaces, and it requires only one matrix-vector product $Av$ per iteration, whereas LSMR would need two. Our numerical experiments with MINRES-QLP and LSMR show that MINARES is a pertinent alternative on consistent symmetric systems and the most suitable Krylov method for inconsistent symmetric systems. We derive properties of MINARES from an equivalent solver named CAR that is to MINARES as CR is to MINRES, is not based on the Lanczos process, and minimizes $\|Ar_k\|$ in the same Krylov subspace as MINARES. We establish that MINARES and CAR generate monotonic $\|x_k - x_{\star}\|$, $\|x_k - x_{\star}\|_A$ and $\|r_k\|$ when $A$ is positive definite.
We derive a family of efficient constrained dynamics algorithms by formulating an equivalent linear quadratic regulator (LQR) problem using Gauss principle of least constraint and solving it using dynamic programming. Our approach builds upon the pioneering (but largely unknown) O(n + m^2d + m^3) solver by Popov and Vereshchagin (PV), where n, m and d are the number of joints, number of constraints and the kinematic tree depth respectively. We provide an expository derivation for the original PV solver and extend it to floating-base kinematic trees with constraints allowed on any link. We make new connections between the LQR's dual Hessian and the inverse operational space inertia matrix (OSIM), permitting efficient OSIM computation, which we further accelerate using matrix inversion lemma. By generalizing the elimination ordering and accounting for MUJOCO-type soft constraints, we derive two original O(n + m) complexity solvers. Our numerical results indicate that significant simulation speed-up can be achieved for high dimensional robots like quadrupeds and humanoids using our algorithms as they scale better than the widely used O(nd^2 + m^2d + d^2m) LTL algorithm of Featherstone. The derivation through the LQR-constrained dynamics connection can make our algorithm accessible to a wider audience and enable cross-fertilization of software and research results between the fields
Given a vector dataset $\mathcal{X}$ and a query vector $\vec{x}_q$, graph-based Approximate Nearest Neighbor Search (ANNS) aims to build a graph index $G$ and approximately return vectors with minimum distances to $\vec{x}_q$ by searching over $G$. The main drawback of graph-based ANNS is that a graph index would be too large to fit into the memory especially for a large-scale $\mathcal{X}$. To solve this, a Product Quantization (PQ)-based hybrid method called DiskANN is proposed to store a low-dimensional PQ index in memory and retain a graph index in SSD, thus reducing memory overhead while ensuring a high search accuracy. However, it suffers from two I/O issues that significantly affect the overall efficiency: (1) long routing path from an entry vertex to the query's neighborhood that results in large number of I/O requests and (2) redundant I/O requests during the routing process. We propose an optimized DiskANN++ to overcome above issues. Specifically, for the first issue, we present a query-sensitive entry vertex selection strategy to replace DiskANN's static graph-central entry vertex by a dynamically determined entry vertex that is close to the query. For the second I/O issue, we present an isomorphic mapping on DiskANN's graph index to optimize the SSD layout and propose an asynchronously optimized Pagesearch based on the optimized SSD layout as an alternative to DiskANN's beamsearch. Comprehensive experimental studies on eight real-world datasets demonstrate our DiskANN++'s superiority on efficiency. We achieve a notable 1.5 X to 2.2 X improvement on QPS compared to DiskANN, given the same accuracy constraint.
We introduce a neural-preconditioned iterative solver for Poisson equations with mixed boundary conditions. The Poisson equation is ubiquitous in scientific computing: it governs a wide array of physical phenomena, arises as a subproblem in many numerical algorithms, and serves as a model problem for the broader class of elliptic PDEs. The most popular Poisson discretizations yield large sparse linear systems. At high resolution, and for performance-critical applications, iterative solvers can be advantageous for these -- but only when paired with powerful preconditioners. The core of our solver is a neural network trained to approximate the inverse of a discrete structured-grid Laplace operator for a domain of arbitrary shape and with mixed boundary conditions. The structure of this problem motivates a novel network architecture that we demonstrate is highly effective as a preconditioner even for boundary conditions outside the training set. We show that on challenging test cases arising from an incompressible fluid simulation, our method outperforms state-of-the-art solvers like algebraic multigrid as well as some recent neural preconditioners.
We provide a collection of results on covariance expressions between Monte Carlo based multi-output mean, variance, and Sobol main effect variance estimators from an ensemble of models. These covariances can be used within multi-fidelity uncertainty quantification strategies that seek to reduce the estimator variance of high-fidelity Monte Carlo estimators with an ensemble of low-fidelity models. Such covariance expressions are required within approaches like the approximate control variate and multi-level best linear unbiased estimator. While the literature provides these expressions for some single-output cases such as mean and variance, our results are relevant to both multiple function outputs and multiple statistics across any sampling strategy. Following the description of these results, we use them within an approximate control variate scheme to show that leveraging multiple outputs can dramatically reduce estimator variance compared to single-output approaches. Synthetic examples are used to highlight the effects of optimal sample allocation and pilot sample estimation. A flight-trajectory simulation of entry, descent, and landing is used to demonstrate multi-output estimation in practical applications.