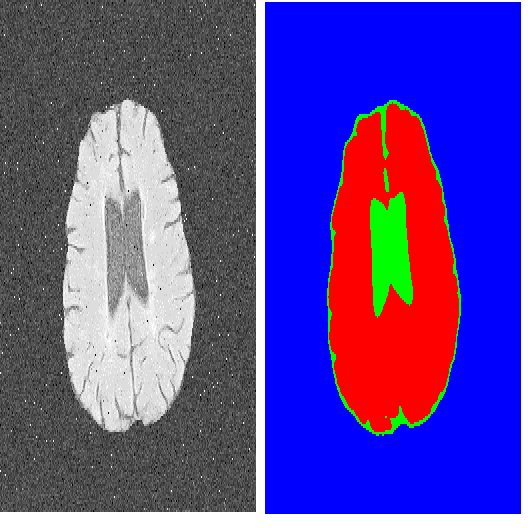
Medical image segmentation is crucial for clinical diagnosis. However, current losses for medical image segmentation mainly focus on overall segmentation results, with fewer losses proposed to guide boundary segmentation. Those that do exist often need to be used in combination with other losses and produce ineffective results. To address this issue, we have developed a simple and effective loss called the Boundary Difference over Union Loss (Boundary DoU Loss) to guide boundary region segmentation. It is obtained by calculating the ratio of the difference set of prediction and ground truth to the union of the difference set and the partial intersection set. Our loss only relies on region calculation, making it easy to implement and training stable without needing any additional losses. Additionally, we use the target size to adaptively adjust attention applied to the boundary regions. Experimental results using UNet, TransUNet, and Swin-UNet on two datasets (ACDC and Synapse) demonstrate the effectiveness of our proposed loss function. Code is available at //github.com/sunfan-bvb/BoundaryDoULoss.
相關內容
We present a distributed conjugate gradient method for distributed optimization problems, where each agent computes an optimal solution of the problem locally without any central computation or coordination, while communicating with its immediate, one-hop neighbors over a communication network. Each agent updates its local problem variable using an estimate of the average conjugate direction across the network, computed via a dynamic consensus approach. Our algorithm enables the agents to use uncoordinated step-sizes. We prove convergence of the local variable of each agent to the optimal solution of the aggregate optimization problem, without requiring decreasing step-sizes. In addition, we demonstrate the efficacy of our algorithm in distributed state estimation problems, and its robust counterparts, where we show its performance compared to existing distributed first-order optimization methods.
Brain tumors are collections of abnormal cells that can develop into masses or clusters. Because they have the potential to infiltrate other tissues, they pose a risk to the patient. The main imaging technique used, MRI, may be able to identify a brain tumor with accuracy. The fast development of Deep Learning methods for use in computer vision applications has been facilitated by a vast amount of training data and improvements in model construction that offer better approximations in a supervised setting. The need for these approaches has been the main driver of this expansion. Deep learning methods have shown promise in improving the precision of brain tumor detection and classification using magnetic resonance imaging (MRI). The study on the use of deep learning techniques, especially ResNet50, for brain tumor identification is presented in this abstract. As a result, this study investigates the possibility of automating the detection procedure using deep learning techniques. In this study, I utilized five transfer learning models which are VGG16, VGG19, DenseNet121, ResNet50 and YOLO V4 where ResNet50 provide the best or highest accuracy 99.54%. The goal of the study is to guide researchers and medical professionals toward powerful brain tumor detecting systems by employing deep learning approaches by way of this evaluation and analysis.
The recent advance of neural fields, such as neural radiance fields, has significantly pushed the boundary of scene representation learning. Aiming to boost the computation efficiency and rendering quality of 3D scenes, a popular line of research maps the 3D coordinate system to another measuring system, e.g., 2D manifolds and hash tables, for modeling neural fields. The conversion of coordinate systems can be typically dubbed as \emph{gauge transformation}, which is usually a pre-defined mapping function, e.g., orthogonal projection or spatial hash function. This begs a question: can we directly learn a desired gauge transformation along with the neural field in an end-to-end manner? In this work, we extend this problem to a general paradigm with a taxonomy of discrete \& continuous cases, and develop a learning framework to jointly optimize gauge transformations and neural fields. To counter the problem that the learning of gauge transformations can collapse easily, we derive a general regularization mechanism from the principle of information conservation during the gauge transformation. To circumvent the high computation cost in gauge learning with regularization, we directly derive an information-invariant gauge transformation which allows to preserve scene information inherently and yield superior performance. Project: //fnzhan.com/Neural-Gauge-Fields
We study a challenging problem of unsupervised discovery of object landmarks. Many recent methods rely on bottlenecks to generate 2D Gaussian heatmaps however, these are limited in generating informed heatmaps while training, presumably due to the lack of effective structural cues. Also, it is assumed that all predicted landmarks are semantically relevant despite having no ground truth supervision. In the current work, we introduce a consistency-guided bottleneck in an image reconstruction-based pipeline that leverages landmark consistency, a measure of compatibility score with the pseudo-ground truth to generate adaptive heatmaps. We propose obtaining pseudo-supervision via forming landmark correspondence across images. The consistency then modulates the uncertainty of the discovered landmarks in the generation of adaptive heatmaps which rank consistent landmarks above their noisy counterparts, providing effective structural information for improved robustness. Evaluations on five diverse datasets including MAFL, AFLW, LS3D, Cats, and Shoes demonstrate excellent performance of the proposed approach compared to the existing state-of-the-art methods. Our code is publicly available at //github.com/MamonaAwan/CGB_ULD.

Purpose: To determine if fine-tuned large language models (LLMs) can generate accurate, personalized impressions for whole-body PET reports. Materials and Methods: Twelve language models were trained on a corpus of PET reports using the teacher-forcing algorithm, with the report findings as input and the clinical impressions as reference. An extra input token encodes the reading physician's identity, allowing models to learn physician-specific reporting styles. Our corpus comprised 37,370 retrospective PET reports collected from our institution between 2010 and 2022. To identify the best LLM, 30 evaluation metrics were benchmarked against quality scores from two nuclear medicine (NM) physicians, with the most aligned metrics selecting the model for expert evaluation. In a subset of data, model-generated impressions and original clinical impressions were assessed by three NM physicians according to 6 quality dimensions and an overall utility score (5-point scale). Each physician reviewed 12 of their own reports and 12 reports from other physicians. Bootstrap resampling was used for statistical analysis. Results: Of all evaluation metrics, domain-adapted BARTScore and PEGASUSScore showed the highest Spearman's rho correlations (0.568 and 0.563) with physician preferences. Based on these metrics, the fine-tuned PEGASUS model was selected as the top LLM. When physicians reviewed PEGASUS-generated impressions in their own style, 89% were considered clinically acceptable, with a mean utility score of 4.08/5. Physicians rated these personalized impressions as comparable in overall utility to the impressions dictated by other physicians (4.03, P=0.41). Conclusion: Personalized impressions generated by PEGASUS were clinically useful, highlighting its potential to expedite PET reporting.
Recent contrastive representation learning methods rely on estimating mutual information (MI) between multiple views of an underlying context. E.g., we can derive multiple views of a given image by applying data augmentation, or we can split a sequence into views comprising the past and future of some step in the sequence. Contrastive lower bounds on MI are easy to optimize, but have a strong underestimation bias when estimating large amounts of MI. We propose decomposing the full MI estimation problem into a sum of smaller estimation problems by splitting one of the views into progressively more informed subviews and by applying the chain rule on MI between the decomposed views. This expression contains a sum of unconditional and conditional MI terms, each measuring modest chunks of the total MI, which facilitates approximation via contrastive bounds. To maximize the sum, we formulate a contrastive lower bound on the conditional MI which can be approximated efficiently. We refer to our general approach as Decomposed Estimation of Mutual Information (DEMI). We show that DEMI can capture a larger amount of MI than standard non-decomposed contrastive bounds in a synthetic setting, and learns better representations in a vision domain and for dialogue generation.
This paper presents a new approach for assembling graph neural networks based on framelet transforms. The latter provides a multi-scale representation for graph-structured data. With the framelet system, we can decompose the graph feature into low-pass and high-pass frequencies as extracted features for network training, which then defines a framelet-based graph convolution. The framelet decomposition naturally induces a graph pooling strategy by aggregating the graph feature into low-pass and high-pass spectra, which considers both the feature values and geometry of the graph data and conserves the total information. The graph neural networks with the proposed framelet convolution and pooling achieve state-of-the-art performance in many types of node and graph prediction tasks. Moreover, we propose shrinkage as a new activation for the framelet convolution, which thresholds the high-frequency information at different scales. Compared to ReLU, shrinkage in framelet convolution improves the graph neural network model in terms of denoising and signal compression: noises in both node and structure can be significantly reduced by accurately cutting off the high-pass coefficients from framelet decomposition, and the signal can be compressed to less than half its original size with the prediction performance well preserved.
Graph neural networks (GNNs) are a popular class of machine learning models whose major advantage is their ability to incorporate a sparse and discrete dependency structure between data points. Unfortunately, GNNs can only be used when such a graph-structure is available. In practice, however, real-world graphs are often noisy and incomplete or might not be available at all. With this work, we propose to jointly learn the graph structure and the parameters of graph convolutional networks (GCNs) by approximately solving a bilevel program that learns a discrete probability distribution on the edges of the graph. This allows one to apply GCNs not only in scenarios where the given graph is incomplete or corrupted but also in those where a graph is not available. We conduct a series of experiments that analyze the behavior of the proposed method and demonstrate that it outperforms related methods by a significant margin.
This paper is an attempt to explain all the matrix calculus you need in order to understand the training of deep neural networks. We assume no math knowledge beyond what you learned in calculus 1, and provide links to help you refresh the necessary math where needed. Note that you do not need to understand this material before you start learning to train and use deep learning in practice; rather, this material is for those who are already familiar with the basics of neural networks, and wish to deepen their understanding of the underlying math. Don't worry if you get stuck at some point along the way---just go back and reread the previous section, and try writing down and working through some examples. And if you're still stuck, we're happy to answer your questions in the Theory category at forums.fast.ai. Note: There is a reference section at the end of the paper summarizing all the key matrix calculus rules and terminology discussed here. See related articles at //explained.ai
The dominant sequence transduction models are based on complex recurrent or convolutional neural networks in an encoder-decoder configuration. The best performing models also connect the encoder and decoder through an attention mechanism. We propose a new simple network architecture, the Transformer, based solely on attention mechanisms, dispensing with recurrence and convolutions entirely. Experiments on two machine translation tasks show these models to be superior in quality while being more parallelizable and requiring significantly less time to train. Our model achieves 28.4 BLEU on the WMT 2014 English-to-German translation task, improving over the existing best results, including ensembles by over 2 BLEU. On the WMT 2014 English-to-French translation task, our model establishes a new single-model state-of-the-art BLEU score of 41.8 after training for 3.5 days on eight GPUs, a small fraction of the training costs of the best models from the literature. We show that the Transformer generalizes well to other tasks by applying it successfully to English constituency parsing both with large and limited training data.