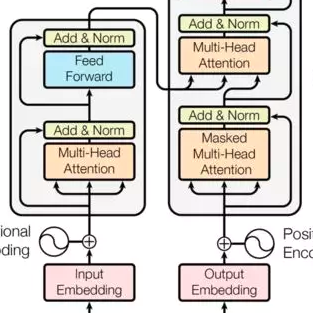
Recent theoretical work has identified surprisingly simple reasoning problems, such as checking if two nodes in a graph are connected or simulating finite-state machines, that are provably unsolvable by standard transformers that answer immediately after reading their input. However, in practice, transformers' reasoning can be improved by allowing them to use a "chain of thought" or "scratchpad", i.e., generate and condition on a sequence of intermediate tokens before answering. Motivated by this, we ask: Does such intermediate generation fundamentally extend the computational power of a decoder-only transformer? We show that the answer is yes, but the amount of increase depends crucially on the amount of intermediate generation. For instance, we find that transformer decoders with a logarithmic number of decoding steps (w.r.t. the input length) push the limits of standard transformers only slightly, while a linear number of decoding steps adds a clear new ability (under standard complexity conjectures): recognizing all regular languages. Our results also imply that linear steps keep transformer decoders within context-sensitive languages, and polynomial steps make them recognize exactly the class of polynomial-time solvable problems -- the first exact characterization of a type of transformers in terms of standard complexity classes. Together, our results provide a nuanced framework for understanding how the length of a transformer's chain of thought or scratchpad impacts its reasoning power.
相關內容
Achievability in information theory refers to demonstrating a coding strategy that accomplishes a prescribed performance benchmark for the underlying task. In quantum information theory, the crafted Hayashi-Nagaoka operator inequality is an essential technique in proving a wealth of one-shot achievability bounds since it effectively resembles a union bound in various problems. In this work, we show that the pretty-good measurement naturally plays a role as the union bound as well. A judicious application of it considerably simplifies the derivation of one-shot achievability for classical-quantum (c-q) channel coding via an elegant three-line proof. The proposed analysis enjoys the following favorable features. (i) The established one-shot bound admits a closed-form expression as in the celebrated Holevo-Helstrom Theorem. Namely, the error probability of sending $M$ messages through a c-q channel is upper bounded by the minimum error of distinguishing the joint channel input-output state against $(M-1)$ decoupled products states. (ii) Our bound directly yields asymptotic results in the large deviation, small deviation, and moderate deviation regimes in a unified manner. (iii) The coefficients incurred in applying the Hayashi-Nagaoka operator inequality are no longer needed. Hence, the derived one-shot bound sharpens existing results relying on the Hayashi-Nagaoka operator inequality. In particular, we obtain the tightest achievable $\epsilon$-one-shot capacity for c-q channel coding heretofore, improving the third-order coding rate in the asymptotic scenario. (iv) Our result holds for infinite-dimensional Hilbert space. (v) The proposed method applies to deriving one-shot achievability for classical data compression with quantum side information, entanglement-assisted classical communication over quantum channels, and various quantum network information-processing protocols.
Although robust statistical estimators are less affected by outlying observations, their computation is usually more challenging. This is particularly the case in high-dimensional sparse settings. The availability of new optimization procedures, mainly developed in the computer science domain, offers new possibilities for the field of robust statistics. This paper investigates how such procedures can be used for robust sparse association estimators. The problem can be split into a robust estimation step followed by an optimization for the remaining decoupled, (bi-)convex problem. A combination of the augmented Lagrangian algorithm and adaptive gradient descent is implemented to also include suitable constraints for inducing sparsity. We provide results concerning the precision of the algorithm and show the advantages over existing algorithms in this context. High-dimensional empirical examples underline the usefulness of this procedure. Extensions to other robust sparse estimators are possible.
State inference and parameter learning in sequential models can be successfully performed with approximation techniques that maximize the evidence lower bound to the marginal log-likelihood of the data distribution. These methods may be referred to as Dynamical Variational Autoencoders, and our specific focus lies on the deep Kalman filter. It has been shown that the ELBO objective can oversimplify data representations, potentially compromising estimation quality. Tighter Monte Carlo objectives have been proposed in the literature to enhance generative modeling performance. For instance, the IWAE objective uses importance weights to reduce the variance of marginal log-likelihood estimates. In this paper, importance sampling is applied to the DKF framework for learning deep Markov models, resulting in the IW-DKF, which shows an improvement in terms of log-likelihood estimates and KL divergence between the variational distribution and the transition model. The framework using the sampled DKF update rule is also accommodated to address sequential state and parameter estimation when working with highly non-linear physics-based models. An experiment with the 3-space Lorenz attractor shows an enhanced generative modeling performance and also a decrease in RMSE when estimating the model parameters and latent states, indicating that tighter MCOs lead to improved state inference performance.
We propose a theory for matrix completion that goes beyond the low-rank structure commonly considered in the literature and applies to general matrices of low description complexity. Specifically, complexity of the sets of matrices encompassed by the theory is measured in terms of Hausdorff and upper Minkowski dimensions. Our goal is the characterization of the number of linear measurements, with an emphasis on rank-$1$ measurements, needed for the existence of an algorithm that yields reconstruction, either perfect, with probability 1, or with arbitrarily small probability of error, depending on the setup. Concretely, we show that matrices taken from a set $\mathcal{U}$ such that $\mathcal{U}-\mathcal{U}$ has Hausdorff dimension $s$ can be recovered from $k>s$ measurements, and random matrices supported on a set $\mathcal{U}$ of Hausdorff dimension $s$ can be recovered with probability 1 from $k>s$ measurements. What is more, we establish the existence of recovery mappings that are robust against additive perturbations or noise in the measurements. Concretely, we show that there are $\beta$-H\"older continuous mappings recovering matrices taken from a set of upper Minkowski dimension $s$ from $k>2s/(1-\beta)$ measurements and, with arbitrarily small probability of error, random matrices supported on a set of upper Minkowski dimension $s$ from $k>s/(1-\beta)$ measurements. The numerous concrete examples we consider include low-rank matrices, sparse matrices, QR decompositions with sparse R-components, and matrices of fractal nature.
In mortality modelling, cohort effects are often taken into consideration as they add insights about variations in mortality across different generations. Statistically speaking, models such as the Renshaw-Haberman model may provide a better fit to historical data compared to their counterparts that incorporate no cohort effects. However, when such models are estimated using an iterative maximum likelihood method in which parameters are updated one at a time, convergence is typically slow and may not even be reached within a reasonably established maximum number of iterations. Among others, the slow convergence problem hinders the study of parameter uncertainty through bootstrapping methods. In this paper, we propose an intuitive estimation method that minimizes the sum of squared errors between actual and fitted log central death rates. The complications arising from the incorporation of cohort effects are overcome by formulating part of the optimization as a principal component analysis with missing values. We also show how the proposed method can be generalized to variants of the Renshaw-Haberman model with further computational improvement, either with a simplified model structure or an additional constraint. Using mortality data from the Human Mortality Database (HMD), we demonstrate that our proposed method produces satisfactory estimation results and is significantly more efficient compared to the traditional likelihood-based approach.
The subrank of tensors is a measure of how much a tensor can be ''diagonalized''. This parameter was introduced by Strassen to study fast matrix multiplication algorithms in algebraic complexity theory and is closely related to many central tensor parameters (e.g. slice rank, partition rank, analytic rank, geometric rank, G-stable rank) and problems in combinatorics, computer science and quantum information theory. Strassen (J. Reine Angew. Math., 1988) proved that there is a gap in the subrank when taking large powers under the tensor product: either the subrank of all powers is at most one, or it grows as a power of a constant strictly larger than one. In this paper, we precisely determine this constant for tensors of any order. Additionally, for tensors of order three, we prove that there is a second gap in the possible rates of growth. Our results strengthen the recent work of Costa and Dalai (J. Comb. Theory, Ser. A, 2021), who proved a similar gap for the slice rank. Our theorem on the subrank has wider applications by implying such gaps not only for the slice rank, but for any ``normalized monotone''. In order to prove the main result, we characterize when a tensor has a very structured tensor (the W-tensor) in its orbit closure. Our methods include degenerations in Grassmanians, which may be of independent interest.
The allure of aesthetic appeal in images captivates our senses, yet the underlying intricacies of aesthetic preferences remain elusive. In this study, we pioneer a novel perspective by utilizing machine learning models that focus on aesthetic attributes known to influence preferences. Through a data mining approach, our models process these attributes as inputs to predict the aesthetic scores of images. Moreover, to delve deeper and obtain interpretable explanations regarding the factors driving aesthetic preferences, we utilize the popular Explainable AI (XAI) technique known as SHapley Additive exPlanations (SHAP). Our methodology involves employing various machine learning models, including Random Forest, XGBoost, Support Vector Regression, and Multilayer Perceptron, to compare their performances in accurately predicting aesthetic scores, and consistently observing results in conjunction with SHAP. We conduct experiments on three image aesthetic benchmarks, providing insights into the roles of attributes and their interactions. Ultimately, our study aims to shed light on the complex nature of aesthetic preferences in images through machine learning and provides a deeper understanding of the attributes that influence aesthetic judgements.
The fusion of causal models with deep learning introducing increasingly intricate data sets, such as the causal associations within images or between textual components, has surfaced as a focal research area. Nonetheless, the broadening of original causal concepts and theories to such complex, non-statistical data has been met with serious challenges. In response, our study proposes redefinitions of causal data into three distinct categories from the standpoint of causal structure and representation: definite data, semi-definite data, and indefinite data. Definite data chiefly pertains to statistical data used in conventional causal scenarios, while semi-definite data refers to a spectrum of data formats germane to deep learning, including time-series, images, text, and others. Indefinite data is an emergent research sphere inferred from the progression of data forms by us. To comprehensively present these three data paradigms, we elaborate on their formal definitions, differences manifested in datasets, resolution pathways, and development of research. We summarize key tasks and achievements pertaining to definite and semi-definite data from myriad research undertakings, present a roadmap for indefinite data, beginning with its current research conundrums. Lastly, we classify and scrutinize the key datasets presently utilized within these three paradigms.
Graph neural networks (GNNs) have been demonstrated to be a powerful algorithmic model in broad application fields for their effectiveness in learning over graphs. To scale GNN training up for large-scale and ever-growing graphs, the most promising solution is distributed training which distributes the workload of training across multiple computing nodes. However, the workflows, computational patterns, communication patterns, and optimization techniques of distributed GNN training remain preliminarily understood. In this paper, we provide a comprehensive survey of distributed GNN training by investigating various optimization techniques used in distributed GNN training. First, distributed GNN training is classified into several categories according to their workflows. In addition, their computational patterns and communication patterns, as well as the optimization techniques proposed by recent work are introduced. Second, the software frameworks and hardware platforms of distributed GNN training are also introduced for a deeper understanding. Third, distributed GNN training is compared with distributed training of deep neural networks, emphasizing the uniqueness of distributed GNN training. Finally, interesting issues and opportunities in this field are discussed.
Object detection typically assumes that training and test data are drawn from an identical distribution, which, however, does not always hold in practice. Such a distribution mismatch will lead to a significant performance drop. In this work, we aim to improve the cross-domain robustness of object detection. We tackle the domain shift on two levels: 1) the image-level shift, such as image style, illumination, etc, and 2) the instance-level shift, such as object appearance, size, etc. We build our approach based on the recent state-of-the-art Faster R-CNN model, and design two domain adaptation components, on image level and instance level, to reduce the domain discrepancy. The two domain adaptation components are based on H-divergence theory, and are implemented by learning a domain classifier in adversarial training manner. The domain classifiers on different levels are further reinforced with a consistency regularization to learn a domain-invariant region proposal network (RPN) in the Faster R-CNN model. We evaluate our newly proposed approach using multiple datasets including Cityscapes, KITTI, SIM10K, etc. The results demonstrate the effectiveness of our proposed approach for robust object detection in various domain shift scenarios.