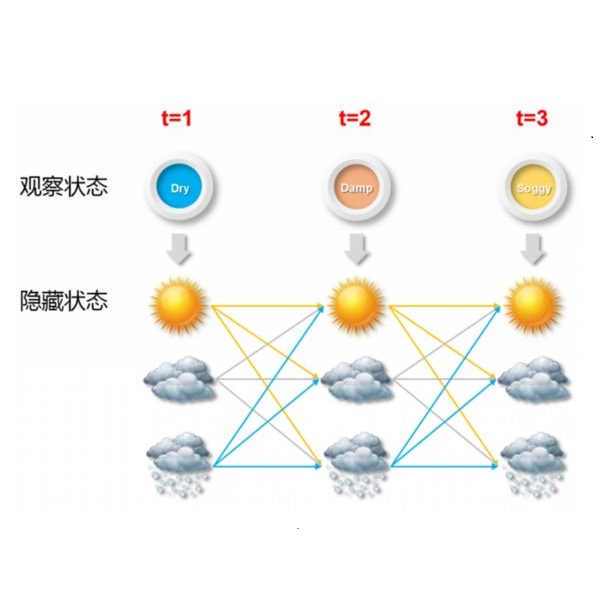
We consider learning the structures of Gaussian latent tree models with vector observations when a subset of them are arbitrarily corrupted. First, we present the sample complexities of Recursive Grouping (RG) and Chow-Liu Recursive Grouping (CLRG) without the assumption that the effective depth is bounded in the number of observed nodes, significantly generalizing the results in Choi et al. (2011). We show that Chow-Liu initialization in CLRG greatly reduces the sample complexity of RG from being exponential in the diameter of the tree to only logarithmic in the diameter for the hidden Markov model (HMM). Second, we robustify RG, CLRG, Neighbor Joining (NJ) and Spectral NJ (SNJ) by using the truncated inner product. These robustified algorithms can tolerate a number of corruptions up to the square root of the number of clean samples. Finally, we derive the first known instance-dependent impossibility result for structure learning of latent trees. The optimalities of the robust version of CLRG and NJ are verified by comparing their sample complexities and the impossibility result.
相關內容
$d$-dimensional (for $d>1$) efficient range-summability ($d$D-ERS) of ideally i.i.d. random variables (RVs) is a fundamental algorithmic problem that has applications to two important families of database problems, namely, fast approximate wavelet tracking (FAWT) on data streams and approximately answering range-sum queries over a data cube. Whether there are efficient solutions to the $d$D-ERS problem, or to the latter database problem, have been two long-standing open problems. Both are solved in this work. Specifically, we propose a novel solution framework to $d$D-ERS on RVs that have Gaussian or Poisson distribution. Our $d$D-ERS solutions are the first ones that have polylogarithmic time complexities. Furthermore, we develop a novel $k$-wise independence theory that allows our $d$D-ERS solutions to have both high computational efficiencies and strong provable independence guarantees. Finally, we show that under a sufficient and likely necessary condition, certain existing solutions for 1D-ERS can be generalized to higher dimensions.
In Bayesian Networks (BNs), the direction of edges is crucial for causal reasoning and inference. However, Markov equivalence class considerations mean it is not always possible to establish edge orientations, which is why many BN structure learning algorithms cannot orientate all edges from purely observational data. Moreover, latent confounders can lead to false positive edges. Relatively few methods have been proposed to address these issues. In this work, we present the hybrid mFGS-BS (majority rule and Fast Greedy equivalence Search with Bayesian Scoring) algorithm for structure learning from discrete data that involves an observational data set and one or more interventional data sets. The algorithm assumes causal insufficiency in the presence of latent variables and produces a Partial Ancestral Graph (PAG). Structure learning relies on a hybrid approach and a novel Bayesian scoring paradigm that calculates the posterior probability of each directed edge being added to the learnt graph. Experimental results based on well-known networks of up to 109 variables and 10k sample size show that mFGS-BS improves structure learning accuracy relative to the state-of-the-art and it is computationally efficient.
The increasing integration of intermittent renewable generation, especially at the distribution level,necessitates advanced planning and optimisation methodologies contingent on the knowledge of thegrid, specifically the admittance matrix capturing the topology and line parameters of an electricnetwork. However, a reliable estimate of the admittance matrix may either be missing or quicklybecome obsolete for temporally varying grids. In this work, we propose a data-driven identificationmethod utilising voltage and current measurements collected from micro-PMUs. More precisely,we first present a maximum likelihood approach and then move towards a Bayesian framework,leveraging the principles of maximum a posteriori estimation. In contrast with most existing con-tributions, our approach not only factors in measurement noise on both voltage and current data,but is also capable of exploiting available a priori information such as sparsity patterns and knownline parameters. Simulations conducted on benchmark cases demonstrate that, compared to otheralgorithms, our method can achieve significantly greater accuracy.
In this paper we present a novel method for learning hierarchical representations of Markov decision processes. Our method works by partitioning the state space into subsets, and defines subtasks for performing transitions between the partitions. We formulate the problem of partitioning the state space as an optimization problem that can be solved using gradient descent given a set of sampled trajectories, making our method suitable for high-dimensional problems with large state spaces. We empirically validate the method, by showing that it can successfully learn a useful hierarchical representation in a navigation domain. Once learned, the hierarchical representation can be used to solve different tasks in the given domain, thus generalizing knowledge across tasks.
Monte Carlo Tree Search (MCTS) is a sampling best-first method to search for optimal decisions. The MCTS's popularity is based on its extraordinary results in the challenging two-player based game Go, a game considered much harder than Chess and that until very recently was considered infeasible for Artificial Intelligence methods. The success of MCTS depends heavily on how the tree is built and the selection process plays a fundamental role in this. One particular selection mechanism that has proved to be reliable is based on the Upper Confidence Bounds for Trees, commonly referred as UCT. The UCT attempts to nicely balance exploration and exploitation by considering the values stored in the statistical tree of the MCTS. However, some tuning of the MCTS UCT is necessary for this to work well. In this work, we use Evolutionary Algorithms (EAs) to evolve mathematical expressions with the goal to substitute the UCT mathematical expression. We compare our proposed approach, called Evolution Strategy in MCTS (ES-MCTS) against five variants of the MCTS UCT, three variants of the star-minimax family of algorithms as well as a random controller in the Game of Carcassonne. We also use a variant of our proposed EA-based controller, dubbed ES partially integrated in MCTS. We show how the ES-MCTS controller, is able to outperform all these 10 intelligent controllers, including robust MCTS UCT controllers.
Motivated by a medical decision making problem, this paper focuses on an impulse control problem for a class of piecewise deterministic semi-Markov processes. The process evolves deterministically between jumps and the inter-jump times have a general distribution. %that may depend on both coordinates. The discrete coordinate (e.g. global health state of the patient) is not observed, the continuous one (e.g. result of some blood measurement) is observed with noise at some (possibly scarce) observation times. The objective %in this paper is to optimally select the observation dates while controlling the process so that it remains close to a nominal value. At each visit to the medical center, a cancer patient undergoes possibly invasive analyses, and {treatment and next visit dates} are scheduled according to their result and the patient history. Frequent observations lead to a better estimation of the hidden state of the process but may be too costly for the center and/or patient. Rare observations may lead to undetected possibly lethal degradation of the patient's health. We exhibit an explicit policy close to optimality based on discretisations of the process. Construction of discretisation grids are discussed at length. The paper is illustrated with experiments on synthetic data fitted from the Intergroupe Francophone du My\'elome 2009 clinical trial.

A common assumption exists according to which machine learning models improve their performance when they have more data to learn from. In this study, the authors wished to clarify the dilemma by performing an empirical experiment utilizing novel vocational student data. The experiment compared different machine learning algorithms while varying the number of data and feature combinations available for training and testing the models. The experiment revealed that the increase of data records or their sample frequency does not immediately lead to significant increases in the model accuracies or performance, however the variance of accuracies does diminish in the case of ensemble models. Similar phenomenon was witnessed while increasing the number of input features for the models. The study refutes the starting assumption and continues to state that in this case the significance in data lies in the quality of the data instead of the quantity of the data.
Learning a graph topology to reveal the underlying relationship between data entities plays an important role in various machine learning and data analysis tasks. Under the assumption that structured data vary smoothly over a graph, the problem can be formulated as a regularised convex optimisation over a positive semidefinite cone and solved by iterative algorithms. Classic methods require an explicit convex function to reflect generic topological priors, e.g. the $\ell_1$ penalty for enforcing sparsity, which limits the flexibility and expressiveness in learning rich topological structures. We propose to learn a mapping from node data to the graph structure based on the idea of learning to optimise (L2O). Specifically, our model first unrolls an iterative primal-dual splitting algorithm into a neural network. The key structural proximal projection is replaced with a variational autoencoder that refines the estimated graph with enhanced topological properties. The model is trained in an end-to-end fashion with pairs of node data and graph samples. Experiments on both synthetic and real-world data demonstrate that our model is more efficient than classic iterative algorithms in learning a graph with specific topological properties.
Machine learning methods are powerful in distinguishing different phases of matter in an automated way and provide a new perspective on the study of physical phenomena. We train a Restricted Boltzmann Machine (RBM) on data constructed with spin configurations sampled from the Ising Hamiltonian at different values of temperature and external magnetic field using Monte Carlo methods. From the trained machine we obtain the flow of iterative reconstruction of spin state configurations to faithfully reproduce the observables of the physical system. We find that the flow of the trained RBM approaches the spin configurations of the maximal possible specific heat which resemble the near criticality region of the Ising model. In the special case of the vanishing magnetic field the trained RBM converges to the critical point of the Renormalization Group (RG) flow of the lattice model. Our results suggest an alternative explanation of how the machine identifies the physical phase transitions, by recognizing certain properties of the configuration like the maximization of the specific heat, instead of associating directly the recognition procedure with the RG flow and its fixed points. Then from the reconstructed data we deduce the critical exponent associated to the magnetization to find satisfactory agreement with the actual physical value. We assume no prior knowledge about the criticality of the system and its Hamiltonian.
The Variational Auto-Encoder (VAE) is one of the most used unsupervised machine learning models. But although the default choice of a Gaussian distribution for both the prior and posterior represents a mathematically convenient distribution often leading to competitive results, we show that this parameterization fails to model data with a latent hyperspherical structure. To address this issue we propose using a von Mises-Fisher (vMF) distribution instead, leading to a hyperspherical latent space. Through a series of experiments we show how such a hyperspherical VAE, or $\mathcal{S}$-VAE, is more suitable for capturing data with a hyperspherical latent structure, while outperforming a normal, $\mathcal{N}$-VAE, in low dimensions on other data types.