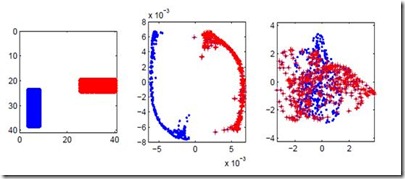
In this paper, we explore how to use topological tools to compare dimension reduction methods. We first make a brief overview of some of the methods often used dimension reduction such as Isometric Feature Mapping, Laplacian Eigenmaps, Fast Independent Component Analysis, Kernel Ridge Regression, t-distributed Stochastic Neighbor Embedding. We then give a brief overview of some topological notions used in topological data analysis, such as, barcodes, persistent homology, and Wasserstein distance. Theoretically, these methods applied on a data set can be interpreted differently. From EEG data embedded into a manifold of high dimension, we apply these methods and we compare them across persistent homologies of dimension 0, 1, and 2, that is, across connected components, tunnels and holes, shells around voids or cavities. We find that from three dimension clouds of points, it is not clear how distinct from each other the methods are, but Wasserstein and Bottleneck distances, topological tests of hypothesis, and various methods show that the methods qualitatively and significantly differ across homologies.
相關內容
Understanding how and why certain communities bear a disproportionate burden of disease is challenging due to the scarcity of data on these communities. Surveys provide a useful avenue for accessing hard-to-reach populations, as many surveys specifically oversample understudied and vulnerable populations. When survey data is used for analysis, it is important to account for the complex survey design that gave rise to the data, in order to avoid biased conclusions. The field of Bayesian survey statistics aims to account for such survey design while leveraging the advantages of Bayesian models, which can flexibly handle sparsity through borrowing of information and provide a coherent inferential framework to easily obtain variances for complex models and data types. For these reasons, Bayesian survey methods seem uniquely well-poised for health disparities research, where heterogeneity and sparsity are frequent considerations. This review discusses three main approaches found in the Bayesian survey methodology literature: 1) multilevel regression and post-stratification, 2) weighted pseudolikelihood-based methods, and 3) synthetic population generation. We discuss advantages and disadvantages of each approach, examine recent applications and extensions, and consider how these approaches may be leveraged to improve research in population health equity.
Recently, Transformer-like deep architectures have shown strong performance on tabular data problems. Unlike traditional models, e.g., MLP, these architectures map scalar values of numerical features to high-dimensional embeddings before mixing them in the main backbone. In this work, we argue that embeddings for numerical features are an underexplored degree of freedom in tabular DL, which allows constructing more powerful DL models and competing with GBDT on some traditionally GBDT-friendly benchmarks. We start by describing two conceptually different approaches to building embedding modules: the first one is based on a piecewise linear encoding of scalar values, and the second one utilizes periodic activations. Then, we empirically demonstrate that these two approaches can lead to significant performance boosts compared to the embeddings based on conventional blocks such as linear layers and ReLU activations. Importantly, we also show that embedding numerical features is beneficial for many backbones, not only for Transformers. Specifically, after proper embeddings, simple MLP-like models can perform on par with the attention-based architectures. Overall, we highlight embeddings for numerical features as an important design aspect with good potential for further improvements in tabular DL.
Gaussian graphical models are nowadays commonly applied to the comparison of groups sharing the same variables, by jointy learning their independence structures. We consider the case where there are exactly two dependent groups and the association structure is represented by a family of coloured Gaussian graphical models suited to deal with paired data problems. To learn the two dependent graphs, together with their across-graph association structure, we implement a fused graphical lasso penalty. We carry out a comprehensive analysis of this approach, with special attention to the role played by some relevant submodel classes. In this way, we provide a broad set of tools for the application of Gaussian graphical models to paired data problems. These include results useful for the specification of penalty values in order to obtain a path of lasso solutions and an ADMM algorithm that solves the fused graphical lasso optimization problem. Finally, we present an application of our method to cancer genomics where it is of interest to compare cancer cells with a control sample from histologically normal tissues adjacent to the tumor. All the methods described in this article are implemented in the $\texttt{R}$ package $\texttt{pdglasso}$ availabe at: //github.com/savranciati/pdglasso.

We present an extended validation of semi-analytical, semi-empirical covariance matrices for the two-point correlation function (2PCF) on simulated catalogs representative of Luminous Red Galaxies (LRG) data collected during the initial two months of operations of the Stage-IV ground-based Dark Energy Spectroscopic Instrument (DESI). We run the pipeline on multiple effective Zel'dovich (EZ) mock galaxy catalogs with the corresponding cuts applied and compare the results with the mock sample covariance to assess the accuracy and its fluctuations. We propose an extension of the previously developed formalism for catalogs processed with standard reconstruction algorithms. We consider methods for comparing covariance matrices in detail, highlighting their interpretation and statistical properties caused by sample variance, in particular, nontrivial expectation values of certain metrics even when the external covariance estimate is perfect. With improved mocks and validation techniques, we confirm a good agreement between our predictions and sample covariance. This allows one to generate covariance matrices for comparable datasets without the need to create numerous mock galaxy catalogs with matching clustering, only requiring 2PCF measurements from the data itself. The code used in this paper is publicly available at //github.com/oliverphilcox/RascalC.
Over the past few years, extensive research has been devoted to enhancing YOLO object detectors. Since its introduction, eight major versions of YOLO have been introduced with the purpose of improving its accuracy and efficiency. While the evident merits of YOLO have yielded to its extensive use in many areas, deploying it on resource-limited devices poses challenges. To address this issue, various neural network compression methods have been developed, which fall under three main categories, namely network pruning, quantization, and knowledge distillation. The fruitful outcomes of utilizing model compression methods, such as lowering memory usage and inference time, make them favorable, if not necessary, for deploying large neural networks on hardware-constrained edge devices. In this review paper, our focus is on pruning and quantization due to their comparative modularity. We categorize them and analyze the practical results of applying those methods to YOLOv5. By doing so, we identify gaps in adapting pruning and quantization for compressing YOLOv5, and provide future directions in this area for further exploration. Among several versions of YOLO, we specifically choose YOLOv5 for its excellent trade-off between recency and popularity in literature. This is the first specific review paper that surveys pruning and quantization methods from an implementation point of view on YOLOv5. Our study is also extendable to newer versions of YOLO as implementing them on resource-limited devices poses the same challenges that persist even today. This paper targets those interested in the practical deployment of model compression methods on YOLOv5, and in exploring different compression techniques that can be used for subsequent versions of YOLO.
The homology groups of a simplicial complex reveal fundamental properties of the topology of the data or the system and the notion of topological stability naturally poses an important yet not fully investigated question. In the current work, we study the stability in terms of the smallest perturbation sufficient to change the dimensionality of the corresponding homology group. Such definition requires an appropriate weighting and normalizing procedure for the boundary operators acting on the Hodge algebra's homology groups. Using the resulting boundary operators, we then formulate the question of structural stability as a spectral matrix nearness problem for the corresponding higher-order graph Laplacian. We develop a bilevel optimization procedure suitable for the formulated matrix nearness problem and illustrate the method's performance on a variety of synthetic quasi-triangulation datasets and transportation networks.
Medical segmentation models are evaluated empirically. As such an evaluation is based on a limited set of example images, it is unavoidably noisy. Beyond a mean performance measure, reporting confidence intervals is thus crucial. However, this is rarely done in medical image segmentation. The width of the confidence interval depends on the test set size and on the spread of the performance measure (its standard-deviation across of the test set). For classification, many test images are needed to avoid wide confidence intervals. Segmentation, however, has not been studied, and it differs by the amount of information brought by a given test image. In this paper, we study the typical confidence intervals in medical image segmentation. We carry experiments on 3D image segmentation using the standard nnU-net framework, two datasets from the Medical Decathlon challenge and two performance measures: the Dice accuracy and the Hausdorff distance. We show that the parametric confidence intervals are reasonable approximations of the bootstrap estimates for varying test set sizes and spread of the performance metric. Importantly, we show that the test size needed to achieve a given precision is often much lower than for classification tasks. Typically, a 1% wide confidence interval requires about 100-200 test samples when the spread is low (standard-deviation around 3%). More difficult segmentation tasks may lead to higher spreads and require over 1000 samples.
We consider the problem of discovering $K$ related Gaussian directed acyclic graphs (DAGs), where the involved graph structures share a consistent causal order and sparse unions of supports. Under the multi-task learning setting, we propose a $l_1/l_2$-regularized maximum likelihood estimator (MLE) for learning $K$ linear structural equation models. We theoretically show that the joint estimator, by leveraging data across related tasks, can achieve a better sample complexity for recovering the causal order (or topological order) than separate estimations. Moreover, the joint estimator is able to recover non-identifiable DAGs, by estimating them together with some identifiable DAGs. Lastly, our analysis also shows the consistency of union support recovery of the structures. To allow practical implementation, we design a continuous optimization problem whose optimizer is the same as the joint estimator and can be approximated efficiently by an iterative algorithm. We validate the theoretical analysis and the effectiveness of the joint estimator in experiments.
Deep models trained in supervised mode have achieved remarkable success on a variety of tasks. When labeled samples are limited, self-supervised learning (SSL) is emerging as a new paradigm for making use of large amounts of unlabeled samples. SSL has achieved promising performance on natural language and image learning tasks. Recently, there is a trend to extend such success to graph data using graph neural networks (GNNs). In this survey, we provide a unified review of different ways of training GNNs using SSL. Specifically, we categorize SSL methods into contrastive and predictive models. In either category, we provide a unified framework for methods as well as how these methods differ in each component under the framework. Our unified treatment of SSL methods for GNNs sheds light on the similarities and differences of various methods, setting the stage for developing new methods and algorithms. We also summarize different SSL settings and the corresponding datasets used in each setting. To facilitate methodological development and empirical comparison, we develop a standardized testbed for SSL in GNNs, including implementations of common baseline methods, datasets, and evaluation metrics.
Lots of learning tasks require dealing with graph data which contains rich relation information among elements. Modeling physics system, learning molecular fingerprints, predicting protein interface, and classifying diseases require that a model to learn from graph inputs. In other domains such as learning from non-structural data like texts and images, reasoning on extracted structures, like the dependency tree of sentences and the scene graph of images, is an important research topic which also needs graph reasoning models. Graph neural networks (GNNs) are connectionist models that capture the dependence of graphs via message passing between the nodes of graphs. Unlike standard neural networks, graph neural networks retain a state that can represent information from its neighborhood with an arbitrary depth. Although the primitive graph neural networks have been found difficult to train for a fixed point, recent advances in network architectures, optimization techniques, and parallel computation have enabled successful learning with them. In recent years, systems based on graph convolutional network (GCN) and gated graph neural network (GGNN) have demonstrated ground-breaking performance on many tasks mentioned above. In this survey, we provide a detailed review over existing graph neural network models, systematically categorize the applications, and propose four open problems for future research.