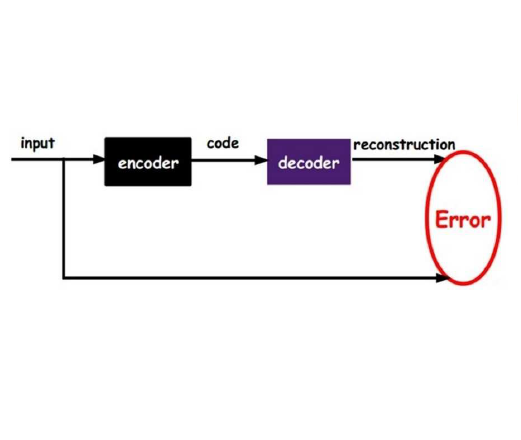
This paper integrates nonlinear-manifold reduced order models (NM-ROMs) with domain decomposition (DD). NM-ROMs approximate the FOM state in a nonlinear-manifold by training a shallow, sparse autoencoder using FOM snapshot data. These NM-ROMs can be advantageous over linear-subspace ROMs (LS-ROMs) for problems with slowly decaying Kolmogorov n-width. However, the number of NM-ROM parameters that need to be trained scales with the size of the FOM. Moreover, for "extreme-scale" problems, the storage of high-dimensional FOM snapshots alone can make ROM training expensive. To alleviate the training cost, this paper applies DD to the FOM, computes NM-ROMs on each subdomain, and couples them to obtain a global NM-ROM. This approach has several advantages: Subdomain NM-ROMs can be trained in parallel, involve fewer parameters to be trained than global NM-ROMs, require smaller subdomain FOM dimensional training data, and can be tailored to subdomain-specific features of the FOM. The shallow, sparse architecture of the autoencoder used in each subdomain NM-ROM allows application of hyper-reduction (HR), reducing the complexity caused by nonlinearity and yielding computational speedup of the NM-ROM. This paper provides the first application of NM-ROM (with HR) to a DD problem. In particular, it details an algebraic DD reformulation of the FOM, trains a NM-ROM with HR for each subdomain, and develops a sequential quadratic programming (SQP) solver to evaluate the coupled global NM-ROM. Theoretical convergence results for the SQP method and a priori and a posteriori error estimates for the DD NM-ROM with HR are provided. The proposed DD NM-ROM with HR approach is numerically compared to a DD LS-ROM with HR on the 2D steady-state Burgers' equation, showing an order of magnitude improvement in accuracy of the proposed DD NM-ROM over the DD LS-ROM.
相關內容
We propose a novel neural network architecture based on conformer transducer that adds contextual information flow to the ASR systems. Our method improves the accuracy of recognizing uncommon words while not harming the word error rate of regular words. We explore the uncommon words accuracy improvement when we use the new model and/or shallow fusion with context language model. We found that combination of both provides cumulative gain in uncommon words recognition accuracy.
Multi-product formulas (MPF) are linear combinations of Trotter circuits offering high-quality simulation of Hamiltonian time evolution with fewer Trotter steps. Here we report two contributions aimed at making multi-product formulas more viable for near-term quantum simulations. First, we extend the theory of Trotter error with commutator scaling developed by Childs, Su, Tran et al. to multi-product formulas. Our result implies that multi-product formulas can achieve a quadratic reduction of Trotter error in 1-norm (nuclear norm) on arbitrary time intervals compared with the regular product formulas without increasing the required circuit depth or qubit connectivity. The number of circuit repetitions grows only by a constant factor. Second, we introduce dynamic multi-product formulas with time-dependent coefficients chosen to minimize a certain efficiently computable proxy for the Trotter error. We use a minimax estimation method to make dynamic multi-product formulas robust to uncertainty from algorithmic errors, sampling and hardware noise. We call this method Minimax MPF and we provide a rigorous bound on its error.
We provide a new theoretical framework for the variable-step deferred correction (DC) methods based on the well-known BDF2 formula. By using the discrete orthogonal convolution kernels, some high-order BDF2-DC methods are proven to be stable on arbitrary time grids according to the recent definition of stability (SINUM, 60: 2253-2272). It significantly relaxes the existing step-ratio restrictions for the BDF2-DC methods (BIT, 62: 1789-1822). The associated sharp error estimates are established by taking the numerical effects of the starting approximations into account, and they suggest that the BDF2-DC methods have no aftereffect, that is, the lower-order starting scheme for the BDF2 scheme will not cause a loss in the accuracy of the high-order BDF2-DC methods. Extensive tests on the graded and random time meshes are presented to support the new theory.
This paper addresses the multiple two-sample test problem in a graph-structured setting, which is a common scenario in fields such as Spatial Statistics and Neuroscience. Each node $v$ in fixed graph deals with a two-sample testing problem between two node-specific probability density functions (pdfs), $p_v$ and $q_v$. The goal is to identify nodes where the null hypothesis $p_v = q_v$ should be rejected, under the assumption that connected nodes would yield similar test outcomes. We propose the non-parametric collaborative two-sample testing (CTST) framework that efficiently leverages the graph structure and minimizes the assumptions over $p_v$ and $q_v$. Our methodology integrates elements from f-divergence estimation, Kernel Methods, and Multitask Learning. We use synthetic experiments and a real sensor network detecting seismic activity to demonstrate that CTST outperforms state-of-the-art non-parametric statistical tests that apply at each node independently, hence disregard the geometry of the problem.
In this paper we develop a Neumann-Neumann type domain decomposition method for elliptic problems on metric graphs. We describe the iteration in the continuous and discrete setting, reformulate the latter in the abstract additive Schwarz framework and prove its convergence to the finite element solution. We provide an implementation and test it on various examples of interest.
We introduce a method for computing immediately human interpretable yet accurate classifiers from tabular data. The classifiers obtained are short DNF-formulas, computed via first discretizing the original data to Boolean form and then using feature selection coupled with a very fast algorithm for producing the best possible Boolean classifier for the setting. We demonstrate the approach via 14 experiments, obtaining results with accuracies mainly similar to ones obtained via random forests, XGBoost, and existing results for the same datasets in the literature. In several cases, our approach in fact outperforms the reference results in relation to accuracy, even though the main objective of our study is the immediate interpretability of our classifiers. We also prove a new result on the probability that the classifier we obtain from real-life data corresponds to the ideally best classifier with respect to the background distribution the data comes from.
An algorithm for three-dimensional dynamic vehicle-track-structure interaction (VTSI) analysis is described in this paper. The algorithm is described in terms of bridges and high-speed trains, but more generally applies to multibody systems coupled to deformable structures by time-varying kinematic constraints. Coupling is accomplished by a kinematic constraint/Lagrange multiplier approach, resulting in a system of index-3 Differential Algebraic Equations (DAE). Three main new concepts are developed. (i) A corotational approach is used to represent the vehicle (train) dynamics. Reference coordinate frames are fitted to the undeformed geometry of the bridge. While the displacements of the train can be large, deformations are taken to be small within these frames, resulting in linear (time-varying) rather than nonlinear dynamics. (ii) If conventional finite elements are used to discretize the track, the curvature is discontinuous across elements (and possibly rotation, too, for curved tracks). This results in spurious numerical oscillations in computed contact forces and accelerations, quantities of key interest in VTSI. A NURBS-based discretization is employed for the track to mitigate such oscillations. (iii) The higher order continuity due to using NURBS allows for alternative techniques for solving the VTSI system. First, enforcing constraints at the acceleration level reduces an index-3 DAE to an index-1 system that can be solved without numerical dissipation. Second, a constraint projection method is proposed to solve an index-3 DAE system without numerical dissipation by correcting wheel velocities and accelerations. Moreover, the modularity of the presented algorithm, resulting from a kinematic constraint/Lagrange multiplier formulation, enables ready integration of this VTSI approach in existing structural analysis and finite element software.
The present work presents a stable POD-Galerkin based reduced-order model (ROM) for two-dimensional Rayleigh-B\'enard convection in a square geometry for three Rayleigh numbers: $10^4$ (steady state), $3\times 10^5$ (periodic), and $6 \times 10^6$ (chaotic). Stability is obtained through a particular (staggered-grid) full-order model (FOM) discretization that leads to a ROM that is pressure-free and has skew-symmetric (energy-conserving) convective terms. This yields long-time stable solutions without requiring stabilizing mechanisms, even outside the training data range. The ROM's stability is validated for the different test cases by investigating the Nusselt and Reynolds number time series and the mean and variance of the vertical temperature profile. In general, these quantities converge to the FOM when increasing the number of modes, and turn out to be a good measure of accuracy. However, for the chaotic case, convergence with increasing numbers of modes is relatively difficult and a high number of modes is required to resolve the low-energy structures that are important for the global dynamics.
The Spatial AutoRegressive model (SAR) is commonly used in studies involving spatial and network data to estimate the spatial or network peer influence and the effects of covariates on the response, taking into account the spatial or network dependence. While the model can be efficiently estimated with a Quasi maximum likelihood approach (QMLE), the detrimental effect of covariate measurement error on the QMLE and how to remedy it is currently unknown. If covariates are measured with error, then the QMLE may not have the $\sqrt{n}$ convergence and may even be inconsistent even when a node is influenced by only a limited number of other nodes or spatial units. We develop a measurement error-corrected ML estimator (ME-QMLE) for the parameters of the SAR model when covariates are measured with error. The ME-QMLE possesses statistical consistency and asymptotic normality properties. We consider two types of applications. The first is when the true covariate cannot be measured directly, and a proxy is observed instead. The second one involves including latent homophily factors estimated with error from the network for estimating peer influence. Our numerical results verify the bias correction property of the estimator and the accuracy of the standard error estimates in finite samples. We illustrate the method on a real dataset related to county-level death rates from the COVID-19 pandemic.
We consider nonparametric Bayesian inference in a multidimensional diffusion model with reflecting boundary conditions based on discrete high-frequency observations. We prove a general posterior contraction rate theorem in $L^2$-loss, which is applied to Gaussian priors. The resulting posteriors, as well as their posterior means, are shown to converge to the ground truth at the minimax optimal rate over H\"older smoothness classes in any dimension. Of independent interest and as part of our proofs, we show that certain frequentist penalized least squares estimators are also minimax optimal.