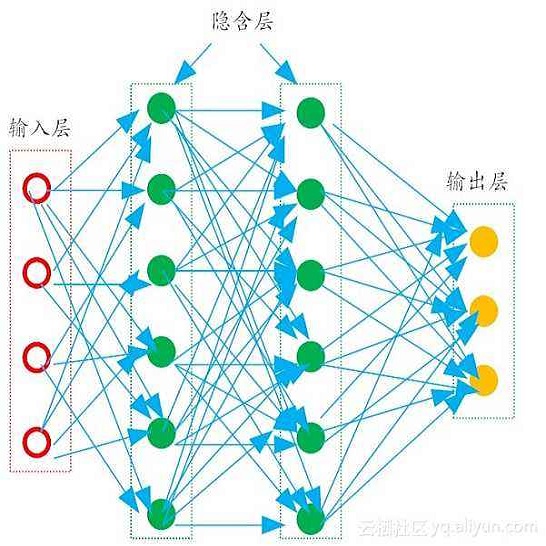
The surrogate model-based uncertainty quantification method has drawn a lot of attention in recent years. Both the polynomial chaos expansion (PCE) and the deep learning (DL) are powerful methods for building a surrogate model. However, the PCE needs to increase the expansion order to improve the accuracy of the surrogate model, which causes more labeled data to solve the expansion coefficients, and the DL also needs a lot of labeled data to train the neural network model. This paper proposes a deep arbitrary polynomial chaos expansion (Deep aPCE) method to improve the balance between surrogate model accuracy and training data cost. On the one hand, the multilayer perceptron (MLP) model is used to solve the adaptive expansion coefficients of arbitrary polynomial chaos expansion, which can improve the Deep aPCE model accuracy with lower expansion order. On the other hand, the adaptive arbitrary polynomial chaos expansion's properties are used to construct the MLP training cost function based on only a small amount of labeled data and a large scale of non-labeled data, which can significantly reduce the training data cost. Four numerical examples and an actual engineering problem are used to verify the effectiveness of the Deep aPCE method.
相關內容
Simulation of the crack network evolution on high strain rate impact experiments performed in brittle materials is very compute-intensive. The cost increases even more if multiple simulations are needed to account for the randomness in crack length, location, and orientation, which is inherently found in real-world materials. Constructing a machine learning emulator can make the process faster by orders of magnitude. There has been little work, however, on assessing the error associated with their predictions. Estimating these errors is imperative for meaningful overall uncertainty quantification. In this work, we extend the heteroscedastic uncertainty estimates to bound a multiple output machine learning emulator. We find that the response prediction is accurate within its predicted errors, but with a somewhat conservative estimate of uncertainty.
Differential dynamic microscopy (DDM) is a form of video image analysis that combines the sensitivity of scattering and the direct visualization benefits of microscopy. DDM is broadly useful in determining dynamical properties including the intermediate scattering function for many spatiotemporally correlated systems. Despite its straightforward analysis, DDM has not been fully adopted as a routine characterization tool, largely due to computational cost and lack of algorithmic robustness. We present statistical analysis that quantifies the noise, reduces the computational order and enhances the robustness of DDM analysis. We propagate the image noise through the Fourier analysis, which allows us to comprehensively study the bias in different estimators of model parameters, and we derive a different way to detect whether the bias is negligible. Furthermore, through use of Gaussian process regression (GPR), we find that predictive samples of the image structure function require only around 0.5%-5% of the Fourier transforms of the observed quantities. This vastly reduces computational cost, while preserving information of the quantities of interest, such as quantiles of the image scattering function, for subsequent analysis. The approach, which we call DDM with uncertainty quantification (DDM-UQ), is validated using both simulations and experiments with respect to accuracy and computational efficiency, as compared with conventional DDM and multiple particle tracking. Overall, we propose that DDM-UQ lays the foundation for important new applications of DDM, as well as to high-throughput characterization. We implement the fast computation tool in a new, publicly available MATLAB software package.

We study problems with stochastic uncertainty information on intervals for which the precise value can be queried by paying a cost. The goal is to devise an adaptive decision tree to find a correct solution to the problem in consideration while minimizing the expected total query cost. We show that, for the sorting problem, such a decision tree can be found in polynomial time. For the problem of finding the data item with minimum value, we have some evidence for hardness. This contradicts intuition, since the minimum problem is easier both in the online setting with adversarial inputs and in the offline verification setting. However, the stochastic assumption can be leveraged to beat both deterministic and randomized approximation lower bounds for the online setting.
Design and operation of complex engineering systems rely on reliability optimization. Such optimization requires us to account for uncertainties expressed in terms of compli-cated, high-dimensional probability distributions, for which only samples or data might be available. However, using data or samples often degrades the computational efficiency, particularly as the conventional failure probability is estimated using the indicator function whose gradient is not defined at zero. To address this issue, by leveraging the buffered failure probability, the paper develops the buffered optimization and reliability method (BORM) for efficient, data-driven optimization of reliability. The proposed formulations, algo-rithms, and strategies greatly improve the computational efficiency of the optimization and thereby address the needs of high-dimensional and nonlinear problems. In addition, an analytical formula is developed to estimate the reliability sensitivity, a subject fraught with difficulty when using the conventional failure probability. The buffered failure probability is thoroughly investigated in the context of many different distributions, leading to a novel measure of tail-heaviness called the buffered tail index. The efficiency and accuracy of the proposed optimization methodology are demonstrated by three numerical examples, which underline the unique advantages of the buffered failure probability for data-driven reliability analysis.
This work presents a new meta-heuristic approach to select the structure of polynomial NARX models for regression and classification problems. The method takes into account the complexity of the model and the contribution of each term to build parsimonious models by proposing a new cost function formulation. The robustness of the new algorithm is tested on several simulated and experimental system with different nonlinear characteristics. The obtained results show that the proposed algorithm is capable of identifying the correct model, for cases where the proper model structure is known, and determine parsimonious models for experimental data even for those systems for which traditional and contemporary methods habitually fails. The new algorithm is validated over classical methods such as the FROLS and recent randomized approaches.
Surface normal estimation from a single image is an important task in 3D scene understanding. In this paper, we address two limitations shared by the existing methods: the inability to estimate the aleatoric uncertainty and lack of detail in the prediction. The proposed network estimates the per-pixel surface normal probability distribution. We introduce a new parameterization for the distribution, such that its negative log-likelihood is the angular loss with learned attenuation. The expected value of the angular error is then used as a measure of the aleatoric uncertainty. We also present a novel decoder framework where pixel-wise multi-layer perceptrons are trained on a subset of pixels sampled based on the estimated uncertainty. The proposed uncertainty-guided sampling prevents the bias in training towards large planar surfaces and improves the quality of prediction, especially near object boundaries and on small structures. Experimental results show that the proposed method outperforms the state-of-the-art in ScanNet and NYUv2, and that the estimated uncertainty correlates well with the prediction error. Code is available at //github.com/baegwangbin/surface_normal_uncertainty.
Due to their increasing spread, confidence in neural network predictions became more and more important. However, basic neural networks do not deliver certainty estimates or suffer from over or under confidence. Many researchers have been working on understanding and quantifying uncertainty in a neural network's prediction. As a result, different types and sources of uncertainty have been identified and a variety of approaches to measure and quantify uncertainty in neural networks have been proposed. This work gives a comprehensive overview of uncertainty estimation in neural networks, reviews recent advances in the field, highlights current challenges, and identifies potential research opportunities. It is intended to give anyone interested in uncertainty estimation in neural networks a broad overview and introduction, without presupposing prior knowledge in this field. A comprehensive introduction to the most crucial sources of uncertainty is given and their separation into reducible model uncertainty and not reducible data uncertainty is presented. The modeling of these uncertainties based on deterministic neural networks, Bayesian neural networks, ensemble of neural networks, and test-time data augmentation approaches is introduced and different branches of these fields as well as the latest developments are discussed. For a practical application, we discuss different measures of uncertainty, approaches for the calibration of neural networks and give an overview of existing baselines and implementations. Different examples from the wide spectrum of challenges in different fields give an idea of the needs and challenges regarding uncertainties in practical applications. Additionally, the practical limitations of current methods for mission- and safety-critical real world applications are discussed and an outlook on the next steps towards a broader usage of such methods is given.
This paper focuses on the expected difference in borrower's repayment when there is a change in the lender's credit decisions. Classical estimators overlook the confounding effects and hence the estimation error can be magnificent. As such, we propose another approach to construct the estimators such that the error can be greatly reduced. The proposed estimators are shown to be unbiased, consistent, and robust through a combination of theoretical analysis and numerical testing. Moreover, we compare the power of estimating the causal quantities between the classical estimators and the proposed estimators. The comparison is tested across a wide range of models, including linear regression models, tree-based models, and neural network-based models, under different simulated datasets that exhibit different levels of causality, different degrees of nonlinearity, and different distributional properties. Most importantly, we apply our approaches to a large observational dataset provided by a global technology firm that operates in both the e-commerce and the lending business. We find that the relative reduction of estimation error is strikingly substantial if the causal effects are accounted for correctly.
Ensembles over neural network weights trained from different random initialization, known as deep ensembles, achieve state-of-the-art accuracy and calibration. The recently introduced batch ensembles provide a drop-in replacement that is more parameter efficient. In this paper, we design ensembles not only over weights, but over hyperparameters to improve the state of the art in both settings. For best performance independent of budget, we propose hyper-deep ensembles, a simple procedure that involves a random search over different hyperparameters, themselves stratified across multiple random initializations. Its strong performance highlights the benefit of combining models with both weight and hyperparameter diversity. We further propose a parameter efficient version, hyper-batch ensembles, which builds on the layer structure of batch ensembles and self-tuning networks. The computational and memory costs of our method are notably lower than typical ensembles. On image classification tasks, with MLP, LeNet, and Wide ResNet 28-10 architectures, our methodology improves upon both deep and batch ensembles.
This work considers the problem of provably optimal reinforcement learning for episodic finite horizon MDPs, i.e. how an agent learns to maximize his/her long term reward in an uncertain environment. The main contribution is in providing a novel algorithm --- Variance-reduced Upper Confidence Q-learning (vUCQ) --- which enjoys a regret bound of $\widetilde{O}(\sqrt{HSAT} + H^5SA)$, where the $T$ is the number of time steps the agent acts in the MDP, $S$ is the number of states, $A$ is the number of actions, and $H$ is the (episodic) horizon time. This is the first regret bound that is both sub-linear in the model size and asymptotically optimal. The algorithm is sub-linear in that the time to achieve $\epsilon$-average regret for any constant $\epsilon$ is $O(SA)$, which is a number of samples that is far less than that required to learn any non-trivial estimate of the transition model (the transition model is specified by $O(S^2A)$ parameters). The importance of sub-linear algorithms is largely the motivation for algorithms such as $Q$-learning and other "model free" approaches. vUCQ algorithm also enjoys minimax optimal regret in the long run, matching the $\Omega(\sqrt{HSAT})$ lower bound. Variance-reduced Upper Confidence Q-learning (vUCQ) is a successive refinement method in which the algorithm reduces the variance in $Q$-value estimates and couples this estimation scheme with an upper confidence based algorithm. Technically, the coupling of both of these techniques is what leads to the algorithm enjoying both the sub-linear regret property and the asymptotically optimal regret.