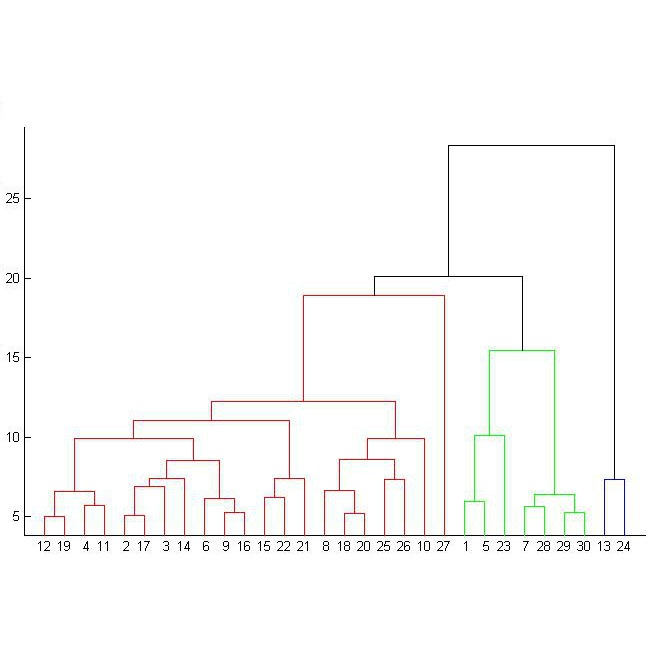
Hierarchical Clustering is a popular unsupervised machine learning method with decades of history and numerous applications. We initiate the study of differentially private approximation algorithms for hierarchical clustering under the rigorous framework introduced by (Dasgupta, 2016). We show strong lower bounds for the problem: that any $\epsilon$-DP algorithm must exhibit $O(|V|^2/ \epsilon)$-additive error for an input dataset $V$. Then, we exhibit a polynomial-time approximation algorithm with $O(|V|^{2.5}/ \epsilon)$-additive error, and an exponential-time algorithm that meets the lower bound. To overcome the lower bound, we focus on the stochastic block model, a popular model of graphs, and, with a separation assumption on the blocks, propose a private $1+o(1)$ approximation algorithm which also recovers the blocks exactly. Finally, we perform an empirical study of our algorithms and validate their performance.
相關內容
Federated learning has gained popularity as a means of training models distributed across the wireless edge. The paper introduces delay-aware federated learning (DFL) to improve the efficiency of distributed machine learning (ML) model training by addressing communication delays between edge and cloud. DFL employs multiple stochastic gradient descent iterations on device datasets during each global aggregation interval and intermittently aggregates model parameters through edge servers in local subnetworks. The cloud server synchronizes the local models with the global deployed model computed via a local-global combiner at global synchronization. The convergence behavior of DFL is theoretically investigated under a generalized data heterogeneity metric. A set of conditions is obtained to achieve the sub-linear convergence rate of O(1/k). Based on these findings, an adaptive control algorithm is developed for DFL, implementing policies to mitigate energy consumption and edge-to-cloud communication latency while aiming for a sublinear convergence rate. Numerical evaluations show DFL's superior performance in terms of faster global model convergence, reduced resource consumption, and robustness against communication delays compared to existing FL algorithms. In summary, this proposed method offers improved efficiency and satisfactory results when dealing with both convex and non-convex loss functions.
The hierarchical small-world network is a real-world network. It models well the benefit transmission web of the pyramid selling in China and many other countries. In this paper, by applying the spectral graph theory, we study three important aspects of the consensus problem in the hierarchical small-world network: convergence speed, communication time-delay robustness, and network coherence. Firstly, we explicitly determine the Laplacian eigenvalues of the hierarchical small-world network by making use of its treelike structure. Secondly, we find that the consensus algorithm on the hierarchical small-world network converges faster than that on some well-studied sparse networks, but is less robust to time delay. The closed-form of the first-order and the second-order network coherence are also derived. Our result shows that the hierarchical small-world network has an optimal structure of noisy consensus dynamics. Therefore, we provide a positive answer to two open questions of Yi \emph{et al}. Finally, we argue that some network structure characteristics, such as large maximum degree, small average path length, and large vertex and edge connectivity, are responsible for the strong robustness with respect to external perturbations.
Recently, several studies consider the stochastic optimization problem but in a heavy-tailed noise regime, i.e., the difference between the stochastic gradient and the true gradient is assumed to have a finite $p$-th moment (say being upper bounded by $\sigma^{p}$ for some $\sigma\geq0$) where $p\in(1,2]$, which not only generalizes the traditional finite variance assumption ($p=2$) but also has been observed in practice for several different tasks. Under this challenging assumption, lots of new progress has been made for either convex or nonconvex problems, however, most of which only consider smooth objectives. In contrast, people have not fully explored and well understood this problem when functions are nonsmooth. This paper aims to fill this crucial gap by providing a comprehensive analysis of stochastic nonsmooth convex optimization with heavy-tailed noises. We revisit a simple clipping-based algorithm, whereas, which is only proved to converge in expectation but under the additional strong convexity assumption. Under appropriate choices of parameters, for both convex and strongly convex functions, we not only establish the first high-probability rates but also give refined in-expectation bounds compared with existing works. Remarkably, all of our results are optimal (or nearly optimal up to logarithmic factors) with respect to the time horizon $T$ even when $T$ is unknown in advance. Additionally, we show how to make the algorithm parameter-free with respect to $\sigma$, in other words, the algorithm can still guarantee convergence without any prior knowledge of $\sigma$.
Motivated by time series forecasting, we study Online Linear Optimization (OLO) under the coupling of two problem structures: the domain is unbounded, and the performance of an algorithm is measured by its dynamic regret. Handling either of them requires the regret bound to depend on certain complexity measure of the comparator sequence -- specifically, the comparator norm in unconstrained OLO, and the path length in dynamic regret. In contrast to a recent work (Jacobsen & Cutkosky, 2022) that adapts to the combination of these two complexity measures, we propose an alternative complexity measure by recasting the problem into sparse coding. Adaptivity can be achieved by a simple modular framework, which naturally exploits more intricate prior knowledge of the environment. Along the way, we also present a new gradient adaptive algorithm for static unconstrained OLO, designed using novel continuous time machinery. This could be of independent interest.
Classic algorithms and machine learning systems like neural networks are both abundant in everyday life. While classic computer science algorithms are suitable for precise execution of exactly defined tasks such as finding the shortest path in a large graph, neural networks allow learning from data to predict the most likely answer in more complex tasks such as image classification, which cannot be reduced to an exact algorithm. To get the best of both worlds, this thesis explores combining both concepts leading to more robust, better performing, more interpretable, more computationally efficient, and more data efficient architectures. The thesis formalizes the idea of algorithmic supervision, which allows a neural network to learn from or in conjunction with an algorithm. When integrating an algorithm into a neural architecture, it is important that the algorithm is differentiable such that the architecture can be trained end-to-end and gradients can be propagated back through the algorithm in a meaningful way. To make algorithms differentiable, this thesis proposes a general method for continuously relaxing algorithms by perturbing variables and approximating the expectation value in closed form, i.e., without sampling. In addition, this thesis proposes differentiable algorithms, such as differentiable sorting networks, differentiable renderers, and differentiable logic gate networks. Finally, this thesis presents alternative training strategies for learning with algorithms.
The conjoining of dynamical systems and deep learning has become a topic of great interest. In particular, neural differential equations (NDEs) demonstrate that neural networks and differential equation are two sides of the same coin. Traditional parameterised differential equations are a special case. Many popular neural network architectures, such as residual networks and recurrent networks, are discretisations. NDEs are suitable for tackling generative problems, dynamical systems, and time series (particularly in physics, finance, ...) and are thus of interest to both modern machine learning and traditional mathematical modelling. NDEs offer high-capacity function approximation, strong priors on model space, the ability to handle irregular data, memory efficiency, and a wealth of available theory on both sides. This doctoral thesis provides an in-depth survey of the field. Topics include: neural ordinary differential equations (e.g. for hybrid neural/mechanistic modelling of physical systems); neural controlled differential equations (e.g. for learning functions of irregular time series); and neural stochastic differential equations (e.g. to produce generative models capable of representing complex stochastic dynamics, or sampling from complex high-dimensional distributions). Further topics include: numerical methods for NDEs (e.g. reversible differential equations solvers, backpropagation through differential equations, Brownian reconstruction); symbolic regression for dynamical systems (e.g. via regularised evolution); and deep implicit models (e.g. deep equilibrium models, differentiable optimisation). We anticipate this thesis will be of interest to anyone interested in the marriage of deep learning with dynamical systems, and hope it will provide a useful reference for the current state of the art.
Sampling methods (e.g., node-wise, layer-wise, or subgraph) has become an indispensable strategy to speed up training large-scale Graph Neural Networks (GNNs). However, existing sampling methods are mostly based on the graph structural information and ignore the dynamicity of optimization, which leads to high variance in estimating the stochastic gradients. The high variance issue can be very pronounced in extremely large graphs, where it results in slow convergence and poor generalization. In this paper, we theoretically analyze the variance of sampling methods and show that, due to the composite structure of empirical risk, the variance of any sampling method can be decomposed into \textit{embedding approximation variance} in the forward stage and \textit{stochastic gradient variance} in the backward stage that necessities mitigating both types of variance to obtain faster convergence rate. We propose a decoupled variance reduction strategy that employs (approximate) gradient information to adaptively sample nodes with minimal variance, and explicitly reduces the variance introduced by embedding approximation. We show theoretically and empirically that the proposed method, even with smaller mini-batch sizes, enjoys a faster convergence rate and entails a better generalization compared to the existing methods.
Clustering is one of the most fundamental and wide-spread techniques in exploratory data analysis. Yet, the basic approach to clustering has not really changed: a practitioner hand-picks a task-specific clustering loss to optimize and fit the given data to reveal the underlying cluster structure. Some types of losses---such as k-means, or its non-linear version: kernelized k-means (centroid based), and DBSCAN (density based)---are popular choices due to their good empirical performance on a range of applications. Although every so often the clustering output using these standard losses fails to reveal the underlying structure, and the practitioner has to custom-design their own variation. In this work we take an intrinsically different approach to clustering: rather than fitting a dataset to a specific clustering loss, we train a recurrent model that learns how to cluster. The model uses as training pairs examples of datasets (as input) and its corresponding cluster identities (as output). By providing multiple types of training datasets as inputs, our model has the ability to generalize well on unseen datasets (new clustering tasks). Our experiments reveal that by training on simple synthetically generated datasets or on existing real datasets, we can achieve better clustering performance on unseen real-world datasets when compared with standard benchmark clustering techniques. Our meta clustering model works well even for small datasets where the usual deep learning models tend to perform worse.
Recently, graph neural networks (GNNs) have revolutionized the field of graph representation learning through effectively learned node embeddings, and achieved state-of-the-art results in tasks such as node classification and link prediction. However, current GNN methods are inherently flat and do not learn hierarchical representations of graphs---a limitation that is especially problematic for the task of graph classification, where the goal is to predict the label associated with an entire graph. Here we propose DiffPool, a differentiable graph pooling module that can generate hierarchical representations of graphs and can be combined with various graph neural network architectures in an end-to-end fashion. DiffPool learns a differentiable soft cluster assignment for nodes at each layer of a deep GNN, mapping nodes to a set of clusters, which then form the coarsened input for the next GNN layer. Our experimental results show that combining existing GNN methods with DiffPool yields an average improvement of 5-10% accuracy on graph classification benchmarks, compared to all existing pooling approaches, achieving a new state-of-the-art on four out of five benchmark data sets.