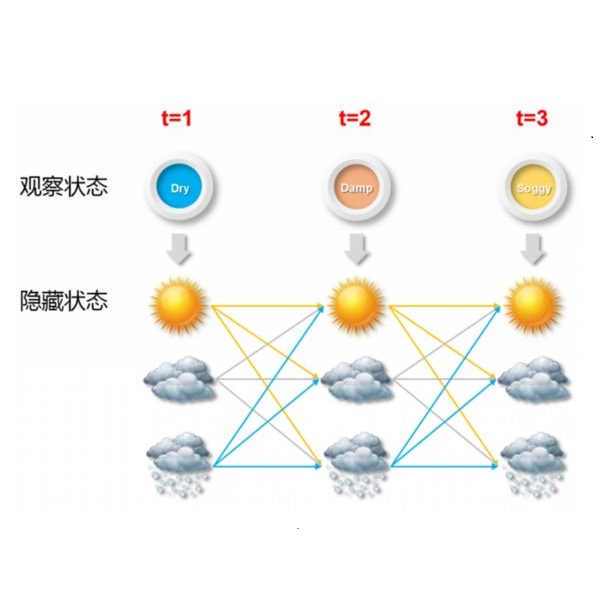
Hidden Markov models (HMMs) and their extensions have proven to be powerful tools for classification of observations that stem from systems with temporal dependence as they take into account that observations close in time are likely generated from the same state (i.e.\ class). When information on the classes of the observations is available in advanced, supervised methods can be applied. In this paper, we provide details for the implementation of four models for classification in a supervised learning context: HMMs, hidden semi-Markov models (HSMMs), autoregressive-HMMs, and autoregressive-HSMMs. Using simulations, we study the classification performance under various degrees of model misspecification to characterize when it would be important to extend a basic HMM to an HSMM. As an application of these techniques we use the models to classify accelerometer data from Merino sheep to distinguish between four different behaviors of interest. In particular in the field of movement ecology, collection of fine-scale animal movement data over time to identify behavioral states has become ubiquitous, necessitating models that can account for the dependence structure in the data. We demonstrate that when the aim is to conduct classification, various degrees of model misspecification of the proposed model may not impede good classification performance unless there is high overlap between the state-dependent distributions, that is, unless the observation distributions of the different states are difficult to differentiate.
相關內容
ACM/IEEE第23屆模型驅動工程語言和系統國際會議，是模型驅動軟件和系統工程的首要會議系列，由ACM-SIGSOFT和IEEE-TCSE支持組織。自1998年以來，模型涵蓋了建模的各個方面，從語言和方法到工具和應用程序。模特的參加者來自不同的背景，包括研究人員、學者、工程師和工業專業人士。MODELS 2019是一個論壇，參與者可以圍繞建模和模型驅動的軟件和系統交流前沿研究成果和創新實踐經驗。今年的版本將為建模社區提供進一步推進建模基礎的機會，并在網絡物理系統、嵌入式系統、社會技術系統、云計算、大數據、機器學習、安全、開源等新興領域提出建模的創新應用以及可持續性。
官網鏈接： ·
馬爾可夫過程
·
推斷
·
CASES
·
蒙特卡羅
·
We construct a family of genealogy-valued Markov processes that are induced by a continuous-time Markov population process. We derive exact expressions for the likelihood of a given genealogy conditional on the history of the underlying population process. These lead to a nonlinear filtering equation which can be used to design efficient Monte Carlo inference algorithms. We demonstrate these calculations with several examples. Existing full-information approaches for phylodynamic inference are special cases of the theory.
In this paper we consider $L_p$-approximation, $p \in \{2,\infty\}$, of periodic functions from weighted Korobov spaces. In particular, we discuss tractability properties of such problems, which means that we aim to relate the dependence of the information complexity on the error demand $\varepsilon$ and the dimension $d$ to the decay rate of the weight sequence $(\gamma_j)_{j \ge 1}$ assigned to the Korobov space. Some results have been well known since the beginning of this millennium, others have been proven quite recently. We give a survey of these findings and will add some new results on the $L_\infty$-approximation problem. To conclude, we give a concise overview of results and collect a number of interesting open problems.
Data collected from wearable devices and smartphones can shed light on an individual's patterns of behavior and circadian routine. Phone use can be modeled as alternating between the state of active use and the state of being idle. Markov chains and alternating recurrent event models are commonly used to model state transitions in cases such as these, and the incorporation of random effects can be used to introduce time-of-day effects. While state labels can be derived prior to modeling dynamics, this approach omits informative regression covariates that can influence state memberships. We instead propose a recurrent event proportional hazards (PH) regression to model the transitions between latent states. We propose an Expectation-Maximization (EM) algorithm for imputing latent state labels and estimating regression parameters. We show that our E-step simplifies to the hidden Markov model (HMM) forward-backward algorithm, allowing us to recover a HMM in addition to PH models. We derive asymptotic distributions for our model parameter estimates and compare our approach against competing methods through simulation as well as in a digital phenotyping study that followed smartphone use in a cohort of adolescents with mood disorders.
Spurred in part by the ever-growing number of sensors and web-based methods of collecting data, the use of Intensive Longitudinal Data (ILD) is becoming more common in the social and behavioural sciences. The ILD collected in this field are often hypothesised to be the result of latent states (e.g. behaviour, emotions), and the promise of ILD lies in its ability to capture the dynamics of these states as they unfold in time. In particular, by collecting data for multiple subjects, researchers can observe how such dynamics differ between subjects. The Bayesian Multilevel Hidden Markov Model (mHMM) is a relatively novel model that is suited to model the ILD of this kind while taking into account heterogeneity between subjects. While the mHMM has been applied in a variety of settings, large-scale studies that examine the required sample size for this model are lacking. In this paper, we address this research gap by conducting a simulation study to evaluate the effect of changing (1) the number of subjects, (2) the number of occasions, and (3) the between subjects variability on parameter estimates obtained by the mHMM. We frame this simulation study in the context of sleep research, which consists of multivariate continuous data that displays considerable overlap in the state dependent component distributions. In addition, we generate a set of baseline scenarios with more general data properties. Overall, the number of subjects has the largest effect on model performance. However, the number of occasions is important to adequately model latent state transitions. We discuss how the characteristics of the data influence parameter estimation and provide recommendations to researchers seeking to apply the mHMM to their own data.
Heterogeneous tabular data are the most commonly used form of data and are essential for numerous critical and computationally demanding applications. On homogeneous data sets, deep neural networks have repeatedly shown excellent performance and have therefore been widely adopted. However, their application to modeling tabular data (inference or generation) remains highly challenging. This work provides an overview of state-of-the-art deep learning methods for tabular data. We start by categorizing them into three groups: data transformations, specialized architectures, and regularization models. We then provide a comprehensive overview of the main approaches in each group. A discussion of deep learning approaches for generating tabular data is complemented by strategies for explaining deep models on tabular data. Our primary contribution is to address the main research streams and existing methodologies in this area, while highlighting relevant challenges and open research questions. To the best of our knowledge, this is the first in-depth look at deep learning approaches for tabular data. This work can serve as a valuable starting point and guide for researchers and practitioners interested in deep learning with tabular data.
AI in finance broadly refers to the applications of AI techniques in financial businesses. This area has been lasting for decades with both classic and modern AI techniques applied to increasingly broader areas of finance, economy and society. In contrast to either discussing the problems, aspects and opportunities of finance that have benefited from specific AI techniques and in particular some new-generation AI and data science (AIDS) areas or reviewing the progress of applying specific techniques to resolving certain financial problems, this review offers a comprehensive and dense roadmap of the overwhelming challenges, techniques and opportunities of AI research in finance over the past decades. The landscapes and challenges of financial businesses and data are firstly outlined, followed by a comprehensive categorization and a dense overview of the decades of AI research in finance. We then structure and illustrate the data-driven analytics and learning of financial businesses and data. The comparison, criticism and discussion of classic vs. modern AI techniques for finance are followed. Lastly, open issues and opportunities address future AI-empowered finance and finance-motivated AI research.
This book develops an effective theory approach to understanding deep neural networks of practical relevance. Beginning from a first-principles component-level picture of networks, we explain how to determine an accurate description of the output of trained networks by solving layer-to-layer iteration equations and nonlinear learning dynamics. A main result is that the predictions of networks are described by nearly-Gaussian distributions, with the depth-to-width aspect ratio of the network controlling the deviations from the infinite-width Gaussian description. We explain how these effectively-deep networks learn nontrivial representations from training and more broadly analyze the mechanism of representation learning for nonlinear models. From a nearly-kernel-methods perspective, we find that the dependence of such models' predictions on the underlying learning algorithm can be expressed in a simple and universal way. To obtain these results, we develop the notion of representation group flow (RG flow) to characterize the propagation of signals through the network. By tuning networks to criticality, we give a practical solution to the exploding and vanishing gradient problem. We further explain how RG flow leads to near-universal behavior and lets us categorize networks built from different activation functions into universality classes. Altogether, we show that the depth-to-width ratio governs the effective model complexity of the ensemble of trained networks. By using information-theoretic techniques, we estimate the optimal aspect ratio at which we expect the network to be practically most useful and show how residual connections can be used to push this scale to arbitrary depths. With these tools, we can learn in detail about the inductive bias of architectures, hyperparameters, and optimizers.
Stream processing has been an active research field for more than 20 years, but it is now witnessing its prime time due to recent successful efforts by the research community and numerous worldwide open-source communities. This survey provides a comprehensive overview of fundamental aspects of stream processing systems and their evolution in the functional areas of out-of-order data management, state management, fault tolerance, high availability, load management, elasticity, and reconfiguration. We review noteworthy past research findings, outline the similarities and differences between early ('00-'10) and modern ('11-'18) streaming systems, and discuss recent trends and open problems.
This paper seeks to develop a deeper understanding of the fundamental properties of neural text generations models. The study of artifacts that emerge in machine generated text as a result of modeling choices is a nascent research area. Previously, the extent and degree to which these artifacts surface in generated text has not been well studied. In the spirit of better understanding generative text models and their artifacts, we propose the new task of distinguishing which of several variants of a given model generated a piece of text, and we conduct an extensive suite of diagnostic tests to observe whether modeling choices (e.g., sampling methods, top-$k$ probabilities, model architectures, etc.) leave detectable artifacts in the text they generate. Our key finding, which is backed by a rigorous set of experiments, is that such artifacts are present and that different modeling choices can be inferred by observing the generated text alone. This suggests that neural text generators may be more sensitive to various modeling choices than previously thought.
Image segmentation is the process of partitioning the image into significant regions easier to analyze. Nowadays, segmentation has become a necessity in many practical medical imaging methods as locating tumors and diseases. Hidden Markov Random Field model is one of several techniques used in image segmentation. It provides an elegant way to model the segmentation process. This modeling leads to the minimization of an objective function. Conjugate Gradient algorithm (CG) is one of the best known optimization techniques. This paper proposes the use of the Conjugate Gradient algorithm (CG) for image segmentation, based on the Hidden Markov Random Field. Since derivatives are not available for this expression, finite differences are used in the CG algorithm to approximate the first derivative. The approach is evaluated using a number of publicly available images, where ground truth is known. The Dice Coefficient is used as an objective criterion to measure the quality of segmentation. The results show that the proposed CG approach compares favorably with other variants of Hidden Markov Random Field segmentation algorithms.
小貼士
登錄享
注冊地址： 北京市海淀區羊坊店路18號2幢3層301-191