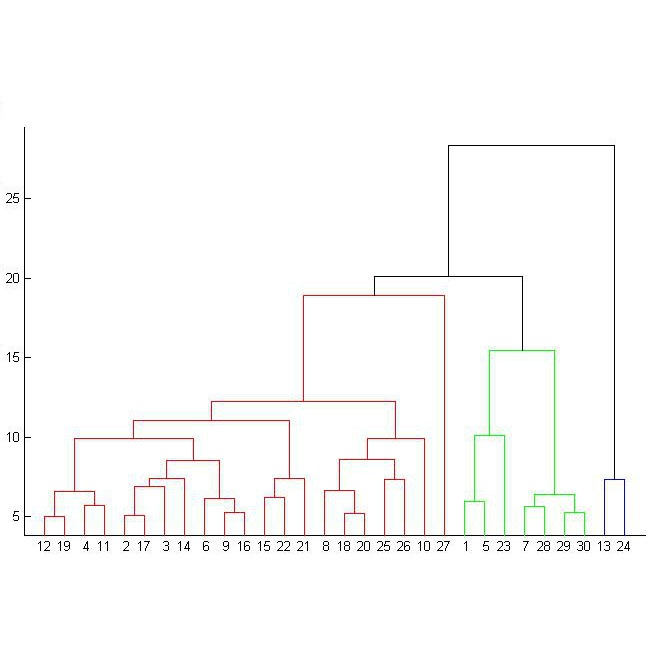
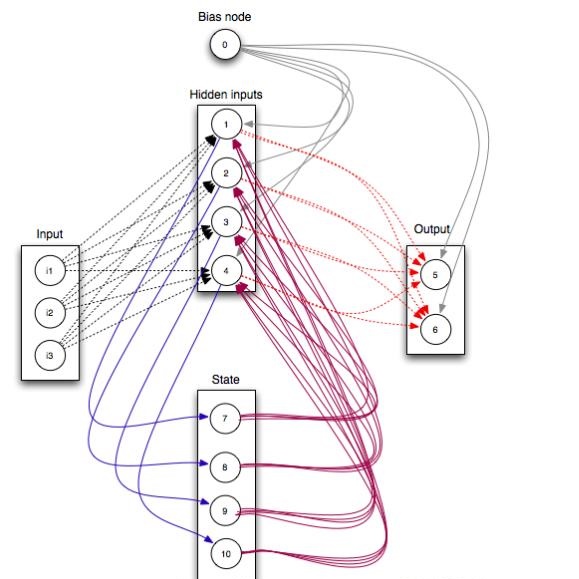
Datasets in the real world are often complex and to some degree hierarchical, with groups and sub-groups of data sharing common characteristics at different levels of abstraction. Understanding and uncovering the hidden structure of these datasets is an important task that has many practical applications. To address this challenge, we present a new and general method for building relational data trees by exploiting the learning dynamics of the Restricted Boltzmann Machine (RBM). Our method is based on the mean-field approach, derived from the Plefka expansion, and developed in the context of disordered systems. It is designed to be easily interpretable. We tested our method in an artificially created hierarchical dataset and on three different real-world datasets (images of digits, mutations in the human genome, and a homologous family of proteins). The method is able to automatically identify the hierarchical structure of the data. This could be useful in the study of homologous protein sequences, where the relationships between proteins are critical for understanding their function and evolution.
相關內容
Federated learning has gained popularity as a means of training models distributed across the wireless edge. The paper introduces delay-aware federated learning (DFL) to improve the efficiency of distributed machine learning (ML) model training by addressing communication delays between edge and cloud. DFL employs multiple stochastic gradient descent iterations on device datasets during each global aggregation interval and intermittently aggregates model parameters through edge servers in local subnetworks. The cloud server synchronizes the local models with the global deployed model computed via a local-global combiner at global synchronization. The convergence behavior of DFL is theoretically investigated under a generalized data heterogeneity metric. A set of conditions is obtained to achieve the sub-linear convergence rate of O(1/k). Based on these findings, an adaptive control algorithm is developed for DFL, implementing policies to mitigate energy consumption and edge-to-cloud communication latency while aiming for a sublinear convergence rate. Numerical evaluations show DFL's superior performance in terms of faster global model convergence, reduced resource consumption, and robustness against communication delays compared to existing FL algorithms. In summary, this proposed method offers improved efficiency and satisfactory results when dealing with both convex and non-convex loss functions.
The hierarchical small-world network is a real-world network. It models well the benefit transmission web of the pyramid selling in China and many other countries. In this paper, by applying the spectral graph theory, we study three important aspects of the consensus problem in the hierarchical small-world network: convergence speed, communication time-delay robustness, and network coherence. Firstly, we explicitly determine the Laplacian eigenvalues of the hierarchical small-world network by making use of its treelike structure. Secondly, we find that the consensus algorithm on the hierarchical small-world network converges faster than that on some well-studied sparse networks, but is less robust to time delay. The closed-form of the first-order and the second-order network coherence are also derived. Our result shows that the hierarchical small-world network has an optimal structure of noisy consensus dynamics. Therefore, we provide a positive answer to two open questions of Yi \emph{et al}. Finally, we argue that some network structure characteristics, such as large maximum degree, small average path length, and large vertex and edge connectivity, are responsible for the strong robustness with respect to external perturbations.
Accurate and robust trajectory prediction of neighboring agents is critical for autonomous vehicles traversing in complex scenes. Most methods proposed in recent years are deep learning-based due to their strength in encoding complex interactions. However, unplausible predictions are often generated since they rely heavily on past observations and cannot effectively capture the transient and contingency interactions from sparse samples. In this paper, we propose a hierarchical hybrid framework of deep learning (DL) and reinforcement learning (RL) for multi-agent trajectory prediction, to cope with the challenge of predicting motions shaped by multi-scale interactions. In the DL stage, the traffic scene is divided into multiple intermediate-scale heterogenous graphs based on which Transformer-style GNNs are adopted to encode heterogenous interactions at intermediate and global levels. In the RL stage, we divide the traffic scene into local sub-scenes utilizing the key future points predicted in the DL stage. To emulate the motion planning procedure so as to produce trajectory predictions, a Transformer-based Proximal Policy Optimization (PPO) incorporated with a vehicle kinematics model is devised to plan motions under the dominant influence of microscopic interactions. A multi-objective reward is designed to balance between agent-centric accuracy and scene-wise compatibility. Experimental results show that our proposal matches the state-of-the-arts on the Argoverse forecasting benchmark. It's also revealed by the visualized results that the hierarchical learning framework captures the multi-scale interactions and improves the feasibility and compliance of the predicted trajectories.
We study the computational complexity of multi-stage robust optimization problems. Such problems are formulated with alternating min/max quantifiers and therefore naturally fall into a higher stage of the polynomial hierarchy. Despite this, almost no hardness results with respect to the polynomial hierarchy are known. In this work, we examine the hardness of robust two-stage adjustable and robust recoverable optimization with budgeted uncertainty sets. Our main technical contribution is the introduction of a technique tailored to prove $\Sigma^p_3$-hardness of such problems. We highlight a difference between continuous and discrete budgeted uncertainty: In the discrete case, indeed a wide range of problems becomes complete for the third stage of the polynomial hierarchy; in particular, this applies to the TSP, independent set, and vertex cover problems. However, in the continuous case this does not happen and problems remain in the first stage of the hierarchy. Finally, if we allow the uncertainty to not only affect the objective, but also multiple constraints, then this distinction disappears and even in the continuous case we encounter hardness for the third stage of the hierarchy. This shows that even robust problems which are already NP-complete can still exhibit a significant computational difference between column-wise and row-wise uncertainty.
Understanding causality helps to structure interventions to achieve specific goals and enables predictions under interventions. With the growing importance of learning causal relationships, causal discovery tasks have transitioned from using traditional methods to infer potential causal structures from observational data to the field of pattern recognition involved in deep learning. The rapid accumulation of massive data promotes the emergence of causal search methods with brilliant scalability. Existing summaries of causal discovery methods mainly focus on traditional methods based on constraints, scores and FCMs, there is a lack of perfect sorting and elaboration for deep learning-based methods, also lacking some considers and exploration of causal discovery methods from the perspective of variable paradigms. Therefore, we divide the possible causal discovery tasks into three types according to the variable paradigm and give the definitions of the three tasks respectively, define and instantiate the relevant datasets for each task and the final causal model constructed at the same time, then reviews the main existing causal discovery methods for different tasks. Finally, we propose some roadmaps from different perspectives for the current research gaps in the field of causal discovery and point out future research directions.
The adaptive processing of structured data is a long-standing research topic in machine learning that investigates how to automatically learn a mapping from a structured input to outputs of various nature. Recently, there has been an increasing interest in the adaptive processing of graphs, which led to the development of different neural network-based methodologies. In this thesis, we take a different route and develop a Bayesian Deep Learning framework for graph learning. The dissertation begins with a review of the principles over which most of the methods in the field are built, followed by a study on graph classification reproducibility issues. We then proceed to bridge the basic ideas of deep learning for graphs with the Bayesian world, by building our deep architectures in an incremental fashion. This framework allows us to consider graphs with discrete and continuous edge features, producing unsupervised embeddings rich enough to reach the state of the art on several classification tasks. Our approach is also amenable to a Bayesian nonparametric extension that automatizes the choice of almost all model's hyper-parameters. Two real-world applications demonstrate the efficacy of deep learning for graphs. The first concerns the prediction of information-theoretic quantities for molecular simulations with supervised neural models. After that, we exploit our Bayesian models to solve a malware-classification task while being robust to intra-procedural code obfuscation techniques. We conclude the dissertation with an attempt to blend the best of the neural and Bayesian worlds together. The resulting hybrid model is able to predict multimodal distributions conditioned on input graphs, with the consequent ability to model stochasticity and uncertainty better than most works. Overall, we aim to provide a Bayesian perspective into the articulated research field of deep learning for graphs.
This PhD thesis contains several contributions to the field of statistical causal modeling. Statistical causal models are statistical models embedded with causal assumptions that allow for the inference and reasoning about the behavior of stochastic systems affected by external manipulation (interventions). This thesis contributes to the research areas concerning the estimation of causal effects, causal structure learning, and distributionally robust (out-of-distribution generalizing) prediction methods. We present novel and consistent linear and non-linear causal effects estimators in instrumental variable settings that employ data-dependent mean squared prediction error regularization. Our proposed estimators show, in certain settings, mean squared error improvements compared to both canonical and state-of-the-art estimators. We show that recent research on distributionally robust prediction methods has connections to well-studied estimators from econometrics. This connection leads us to prove that general K-class estimators possess distributional robustness properties. We, furthermore, propose a general framework for distributional robustness with respect to intervention-induced distributions. In this framework, we derive sufficient conditions for the identifiability of distributionally robust prediction methods and present impossibility results that show the necessity of several of these conditions. We present a new structure learning method applicable in additive noise models with directed trees as causal graphs. We prove consistency in a vanishing identifiability setup and provide a method for testing substructure hypotheses with asymptotic family-wise error control that remains valid post-selection. Finally, we present heuristic ideas for learning summary graphs of nonlinear time-series models.
Graph Neural Networks (GNNs) draw their strength from explicitly modeling the topological information of structured data. However, existing GNNs suffer from limited capability in capturing the hierarchical graph representation which plays an important role in graph classification. In this paper, we innovatively propose hierarchical graph capsule network (HGCN) that can jointly learn node embeddings and extract graph hierarchies. Specifically, disentangled graph capsules are established by identifying heterogeneous factors underlying each node, such that their instantiation parameters represent different properties of the same entity. To learn the hierarchical representation, HGCN characterizes the part-whole relationship between lower-level capsules (part) and higher-level capsules (whole) by explicitly considering the structure information among the parts. Experimental studies demonstrate the effectiveness of HGCN and the contribution of each component.
There has been appreciable progress in unsupervised network representation learning (UNRL) approaches over graphs recently with flexible random-walk approaches, new optimization objectives and deep architectures. However, there is no common ground for systematic comparison of embeddings to understand their behavior for different graphs and tasks. In this paper we theoretically group different approaches under a unifying framework and empirically investigate the effectiveness of different network representation methods. In particular, we argue that most of the UNRL approaches either explicitly or implicit model and exploit context information of a node. Consequently, we propose a framework that casts a variety of approaches -- random walk based, matrix factorization and deep learning based -- into a unified context-based optimization function. We systematically group the methods based on their similarities and differences. We study the differences among these methods in detail which we later use to explain their performance differences (on downstream tasks). We conduct a large-scale empirical study considering 9 popular and recent UNRL techniques and 11 real-world datasets with varying structural properties and two common tasks -- node classification and link prediction. We find that there is no single method that is a clear winner and that the choice of a suitable method is dictated by certain properties of the embedding methods, task and structural properties of the underlying graph. In addition we also report the common pitfalls in evaluation of UNRL methods and come up with suggestions for experimental design and interpretation of results.