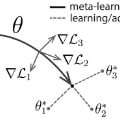
In the paper, we propose an effective and efficient Compositional Federated Learning (ComFedL) algorithm for solving a new compositional Federated Learning (FL) framework, which frequently appears in many data mining and machine learning problems with a hierarchical structure such as distributionally robust FL and model-agnostic meta learning (MAML). Moreover, we study the convergence analysis of our ComFedL algorithm under some mild conditions, and prove that it achieves a convergence rate of $O(\frac{1}{\sqrt{T}})$, where $T$ denotes the number of iteration. To the best of our knowledge, our new Compositional FL framework is the first work to bridge federated learning with composition stochastic optimization. In particular, we first transform the distributionally robust FL (i.e., a minimax optimization problem) into a simple composition optimization problem by using KL divergence regularization. At the same time, we also first transform the distribution-agnostic MAML problem (i.e., a minimax optimization problem) into a simple yet effective composition optimization problem. Finally, we apply two popular machine learning tasks, i.e., distributionally robust FL and MAML to demonstrate the effectiveness of our algorithm.
相關內容
Quantum neural networks (QNNs) and quantum kernels stand as prominent figures in the realm of quantum machine learning, poised to leverage the nascent capabilities of near-term quantum computers to surmount classical machine learning challenges. Nonetheless, the training efficiency challenge poses a limitation on both QNNs and quantum kernels, curbing their efficacy when applied to extensive datasets. To confront this concern, we present a unified approach: coreset selection, aimed at expediting the training of QNNs and quantum kernels by distilling a judicious subset from the original training dataset. Furthermore, we analyze the generalization error bounds of QNNs and quantum kernels when trained on such coresets, unveiling the comparable performance with those training on the complete original dataset. Through systematic numerical simulations, we illuminate the potential of coreset selection in expediting tasks encompassing synthetic data classification, identification of quantum correlations, and quantum compiling. Our work offers a useful way to improve diverse quantum machine learning models with a theoretical guarantee while reducing the training cost.
In this paper, we introduce an improved version of the fifth-order weighted essentially non-oscillatory (WENO) shock-capturing scheme by incorporating deep learning techniques. The established WENO algorithm is improved by training a compact neural network to adjust the smoothness indicators within the WENO scheme. This modification enhances the accuracy of the numerical results, particularly near abrupt shocks. Unlike previous deep learning-based methods, no additional post-processing steps are necessary for maintaining consistency. We demonstrate the superiority of our new approach using several examples from the literature for the two-dimensional Euler equations of gas dynamics. Through intensive study of these test problems, which involve various shocks and rarefaction waves, the new technique is shown to outperform traditional fifth-order WENO schemes, especially in cases where the numerical solutions exhibit excessive diffusion or overshoot around shocks.
In this work, we construct a fifth-order weighted essentially non-oscillatory (WENO) scheme with exponential approximation space for solving dispersive equations. A conservative third-order derivative formulation is developed directly using WENO spatial reconstruction procedure and third-order TVD Runge- Kutta scheme is used for the evaluation of time derivative. This exponential approximation space consists a tension parameter that may be optimized to fit the specific feature of the charecteristic data, yielding better results without spurious oscillations compared to the polynomial approximation space. A detailed formulation is presented for the the construction of conservative flux approximation, smoothness indicators, nonlinear weights and verified that the proposed scheme provides the required fifth convergence order. One and two-dimensional numerical examples are presented to support the theoretical claims.
We present a robust deep incremental learning framework for regression tasks on financial temporal tabular datasets which is built upon the incremental use of commonly available tabular and time series prediction models to adapt to distributional shifts typical of financial datasets. The framework uses a simple basic building block (decision trees) to build self-similar models of any required complexity to deliver robust performance under adverse situations such as regime changes, fat-tailed distributions, and low signal-to-noise ratios. As a detailed study, we demonstrate our scheme using XGBoost models trained on the Numerai dataset and show that a two layer deep ensemble of XGBoost models over different model snapshots delivers high quality predictions under different market regimes. We also show that the performance of XGBoost models with different number of boosting rounds in three scenarios (small, standard and large) is monotonically increasing with respect to model size and converges towards the generalisation upper bound. We also evaluate the robustness of the model under variability of different hyperparameters, such as model complexity and data sampling settings. Our model has low hardware requirements as no specialised neural architectures are used and each base model can be independently trained in parallel.
In this paper, we combine the Smolyak technique for multi-dimensional interpolation with the Filon-Clenshaw-Curtis (FCC) rule for one-dimensional oscillatory integration, to obtain a new Filon-Clenshaw-Curtis-Smolyak (FCCS) rule for oscillatory integrals with linear phase over the $d-$dimensional cube $[-1,1]^d$. By combining stability and convergence estimates for the FCC rule with error estimates for the Smolyak interpolation operator, we obtain an error estimate for the FCCS rule, consisting of the product of a Smolyak-type error estimate multiplied by a term that decreases with $\mathcal{O}(k^{-\tilde{d}})$, where $k$ is the wavenumber and $\tilde{d}$ is the number of oscillatory dimensions. If all dimensions are oscillatory, a higher negative power of $k$ appears in the estimate. As an application, we consider the forward problem of uncertainty quantification (UQ) for a one-space-dimensional Helmholtz problem with wavenumber $k$ and a random heterogeneous refractive index, depending in an affine way on $d$ i.i.d. uniform random variables. After applying a classical hybrid numerical-asymptotic approximation, expectations of functionals of the solution of this problem can be formulated as a sum of oscillatory integrals over $[-1,1]^d$, which we compute using the FCCS rule. We give numerical results for the FCCS rule and the UQ algorithm showing that accuracy improves when both $k$ and the order of the rule increase. We also give results for dimension-adaptive sparse grid FCCS quadrature showing its efficiency as dimension increases.
We discuss techniques of estimation and inference for nonlinear cohort panels with learning from experience, showing, inter alia, the consistency and asymptotic normality of the nonlinear least squares estimator employed in the seminal paper by Malmendier and Nagel (2016). Potential pitfalls for hypothesis testing are identified and solutions proposed. Monte Carlo simulations verify the properties of the estimator and corresponding test statistics in finite samples, while an application to a panel of survey expectations demonstrates the usefulness of the theory developed.
The accurate representation of precipitation in Earth system models (ESMs) is crucial for reliable projections of the ecological and socioeconomic impacts in response to anthropogenic global warming. The complex cross-scale interactions of processes that produce precipitation are challenging to model, however, inducing potentially strong biases in ESM fields, especially regarding extremes. State-of-the-art bias correction methods only address errors in the simulated frequency distributions locally at every individual grid cell. Improving unrealistic spatial patterns of the ESM output, which would require spatial context, has not been possible so far. Here, we show that a post-processing method based on physically constrained generative adversarial networks (cGANs) can correct biases of a state-of-the-art, CMIP6-class ESM both in local frequency distributions and in the spatial patterns at once. While our method improves local frequency distributions equally well as gold-standard bias-adjustment frameworks, it strongly outperforms any existing methods in the correction of spatial patterns, especially in terms of the characteristic spatial intermittency of precipitation extremes.
The notion that algorithmic systems should be "transparent" and "explainable" is common in the many statements of consensus principles developed by governments, companies, and advocacy organizations. But what exactly do policy and legal actors want from these technical concepts, and how do their desiderata compare with the explainability techniques developed in the machine learning literature? In hopes of better connecting the policy and technical communities, we provide case studies illustrating five ways in which algorithmic transparency and explainability have been used in policy settings: specific requirements for explanations; in nonbinding guidelines for internal governance of algorithms; in regulations applicable to highly regulated settings; in guidelines meant to increase the utility of legal liability for algorithms; and broad requirements for model and data transparency. The case studies span a spectrum from precise requirements for specific types of explanations to nonspecific requirements focused on broader notions of transparency, illustrating the diverse needs, constraints, and capacities of various policy actors and contexts. Drawing on these case studies, we discuss promising ways in which transparency and explanation could be used in policy, as well as common factors limiting policymakers' use of algorithmic explainability. We conclude with recommendations for researchers and policymakers.
This paper proposes a method for extracting a lightweight subset from a text-to-speech (TTS) corpus ensuring synthetic speech quality. In recent years, methods have been proposed for constructing large-scale TTS corpora by collecting diverse data from massive sources such as audiobooks and YouTube. Although these methods have gained significant attention for enhancing the expressive capabilities of TTS systems, they often prioritize collecting vast amounts of data without considering practical constraints like storage capacity and computation time in training, which limits the available data quantity. Consequently, the need arises to efficiently collect data within these volume constraints. To address this, we propose a method for selecting the core subset~(known as \textit{core-set}) from a TTS corpus on the basis of a \textit{diversity metric}, which measures the degree to which a subset encompasses a wide range. Experimental results demonstrate that our proposed method performs significantly better than the baseline phoneme-balanced data selection across language and corpus size.
The goal of explainable Artificial Intelligence (XAI) is to generate human-interpretable explanations, but there are no computationally precise theories of how humans interpret AI generated explanations. The lack of theory means that validation of XAI must be done empirically, on a case-by-case basis, which prevents systematic theory-building in XAI. We propose a psychological theory of how humans draw conclusions from saliency maps, the most common form of XAI explanation, which for the first time allows for precise prediction of explainee inference conditioned on explanation. Our theory posits that absent explanation humans expect the AI to make similar decisions to themselves, and that they interpret an explanation by comparison to the explanations they themselves would give. Comparison is formalized via Shepard's universal law of generalization in a similarity space, a classic theory from cognitive science. A pre-registered user study on AI image classifications with saliency map explanations demonstrate that our theory quantitatively matches participants' predictions of the AI.