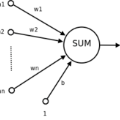
Interpretability of neural networks and their underlying theoretical behavior remain an open field of study even after the great success of their practical applications, particularly with the emergence of deep learning. In this work, NN2Poly is proposed: a theoretical approach to obtain an explicit polynomial model that provides an accurate representation of an already trained fully-connected feed-forward artificial neural network (a multilayer perceptron or MLP). This approach extends a previous idea proposed in the literature, which was limited to single hidden layer networks, to work with arbitrarily deep MLPs in both regression and classification tasks. The objective of this paper is to achieve this by using a Taylor expansion on the activation function, at each layer, and then using several combinatorial properties to calculate the coefficients of the desired polynomials. Discussion is presented on the main computational challenges of this method, and the way to overcome them by imposing certain constraints during the training phase. Finally, simulation experiments as well as an application to a real data set are presented to demonstrate the effectiveness of the proposed method.
相關內容
Owing to the data explosion and rapid development of artificial intelligence (AI), particularly deep neural networks (DNNs), the ever-increasing demand for large-scale matrix-vector multiplication has become one of the major issues in machine learning (ML). Training and evaluating such neural networks rely on heavy computational resources, resulting in significant system latency and power consumption. To overcome these issues, analog computing using optical interferometric-based linear processors have recently appeared as promising candidates in accelerating matrix-vector multiplication and lowering power consumption. On the other hand, radio frequency (RF) electromagnetic waves can also exhibit similar advantages as the optical counterpart by performing analog computation at light speed with lower power. Furthermore, RF devices have extra benefits such as lower cost, mature fabrication, and analog-digital mixed design simplicity, which has great potential in realizing affordable, scalable, low latency, low power, near-sensor radio frequency neural network (RFNN) that may greatly enrich RF signal processing capability. In this work, we propose a 2X2 reconfigurable linear RF analog processor in theory and experiment, which can be applied as a matrix multiplier in an artificial neural network (ANN). The proposed device can be utilized to realize a 2X2 simple RFNN for data classification. An 8X8 linear analog processor formed by 28 RFNN devices are also applied in a 4-layer ANN for Modified National Institute of Standards and Technology (MNIST) dataset classification.
For Deep Neural Networks (DNNs) to become useful in safety-critical applications, such as self-driving cars and disease diagnosis, they must be stable to perturbations in input and model parameters. Characterizing the sensitivity of a DNN to perturbations is necessary to determine minimal bit-width precision that may be used to safely represent the network. However, no general result exists that is capable of predicting the sensitivity of a given DNN to round-off error, noise, or other perturbations in input. This paper derives an estimator that can predict such quantities. The estimator is derived via inequalities and matrix norms, and the resulting quantity is roughly analogous to a condition number for the entire neural network. An approximation of the estimator is tested on two Convolutional Neural Networks, AlexNet and VGG-19, using the ImageNet dataset. For each of these networks, the tightness of the estimator is explored via random perturbations and adversarial attacks.
Summation-by-parts (SBP) operators allow us to systematically develop energy-stable and high-order accurate numerical methods for time-dependent differential equations. Until recently, the main idea behind existing SBP operators was that polynomials can accurately approximate the solution, and SBP operators should thus be exact for them. However, polynomials do not provide the best approximation for some problems, with other approximation spaces being more appropriate. We recently addressed this issue and developed a theory for one-dimensional SBP operators based on general function spaces, coined function-space SBP (FSBP) operators. In this paper, we extend the theory of FSBP operators to multiple dimensions. We focus on their existence, connection to quadratures, construction, and mimetic properties. A more exhaustive numerical demonstration of multi-dimensional FSBP (MFSBP) operators and their application will be provided in future works. Similar to the one-dimensional case, we demonstrate that most of the established results for polynomial-based multi-dimensional SBP (MSBP) operators carry over to the more general class of MFSBP operators. Our findings imply that the concept of SBP operators can be applied to a significantly larger class of methods than is currently done. This can increase the accuracy of the numerical solutions and/or provide stability to the methods.
In this paper, we introduce a type of tensor neural network. For the first time, we propose its numerical integration scheme and prove the computational complexity to be the polynomial scale of the dimension. Based on the tensor product structure, we develop an efficient numerical integration method by using fixed quadrature points for the functions of the tensor neural network. The corresponding machine learning method is also introduced for solving high-dimensional problems. Some numerical examples are also provided to validate the theoretical results and the numerical algorithm.
One of the fundamental problems in machine learning is generalization. In neural network models with a large number of weights (parameters), many solutions can be found to fit the training data equally well. The key question is which solution can describe testing data not in the training set. Here, we report the discovery of an exact duality (equivalence) between changes in activities in a given layer of neurons and changes in weights that connect to the next layer of neurons in a densely connected layer in any feed forward neural network. The activity-weight (A-W) duality allows us to map variations in inputs (data) to variations of the corresponding dual weights. By using this mapping, we show that the generalization loss can be decomposed into a sum of contributions from different eigen-directions of the Hessian matrix of the loss function at the solution in weight space. The contribution from a given eigen-direction is the product of two geometric factors (determinants): the sharpness of the loss landscape and the standard deviation of the dual weights, which is found to scale with the weight norm of the solution. Our results provide an unified framework, which we used to reveal how different regularization schemes (weight decay, stochastic gradient descent with different batch sizes and learning rates, dropout), training data size, and labeling noise affect generalization performance by controlling either one or both of these two geometric determinants for generalization. These insights can be used to guide development of algorithms for finding more generalizable solutions in overparametrized neural networks.
Understanding dynamics in complex systems is challenging because there are many degrees of freedom, and those that are most important for describing events of interest are often not obvious. The leading eigenfunctions of the transition operator are useful for visualization, and they can provide an efficient basis for computing statistics such as the likelihood and average time of events (predictions). Here we develop inexact iterative linear algebra methods for computing these eigenfunctions (spectral estimation) and making predictions from a data set of short trajectories sampled at finite intervals. We demonstrate the methods on a low-dimensional model that facilitates visualization and a high-dimensional model of a biomolecular system. Implications for the prediction problem in reinforcement learning are discussed.
Large language models (LLMs) have demonstrated remarkable proficiency in understanding and generating human-like texts, which may potentially revolutionize the finance industry. However, existing LLMs often fall short in the financial field, which is mainly attributed to the disparities between general text data and financial text data. Unfortunately, there is only a limited number of financial text datasets available (quite small size), and BloombergGPT, the first financial LLM (FinLLM), is close-sourced (only the training logs were released). In light of this, we aim to democratize Internet-scale financial data for LLMs, which is an open challenge due to diverse data sources, low signal-to-noise ratio, and high time-validity. To address the challenges, we introduce an open-sourced and data-centric framework, \textit{Financial Generative Pre-trained Transformer (FinGPT)}, that automates the collection and curation of real-time financial data from >34 diverse sources on the Internet, providing researchers and practitioners with accessible and transparent resources to develop their FinLLMs. Additionally, we propose a simple yet effective strategy for fine-tuning FinLLM using the inherent feedback from the market, dubbed Reinforcement Learning with Stock Prices (RLSP). We also adopt the Low-rank Adaptation (LoRA, QLoRA) method that enables users to customize their own FinLLMs from open-source general-purpose LLMs at a low cost. Finally, we showcase several FinGPT applications, including robo-advisor, sentiment analysis for algorithmic trading, and low-code development. FinGPT aims to democratize FinLLMs, stimulate innovation, and unlock new opportunities in open finance. The codes are available at //github.com/AI4Finance-Foundation/FinGPT and //github.com/AI4Finance-Foundation/FinNLP
In this thesis, we explore the use of complex systems to study learning and adaptation in natural and artificial systems. The goal is to develop autonomous systems that can learn without supervision, develop on their own, and become increasingly complex over time. Complex systems are identified as a suitable framework for understanding these phenomena due to their ability to exhibit growth of complexity. Being able to build learning algorithms that require limited to no supervision would enable greater flexibility and adaptability in various applications. By understanding the fundamental principles of learning in complex systems, we hope to advance our ability to design and implement practical learning algorithms in the future. This thesis makes the following key contributions: the development of a general complexity metric that we apply to search for complex systems that exhibit growth of complexity, the introduction of a coarse-graining method to study computations in large-scale complex systems, and the development of a metric for learning efficiency as well as a benchmark dataset for evaluating the speed of learning algorithms. Our findings add substantially to our understanding of learning and adaptation in natural and artificial systems. Moreover, our approach contributes to a promising new direction for research in this area. We hope these findings will inspire the development of more effective and efficient learning algorithms in the future.
As soon as abstract mathematical computations were adapted to computation on digital computers, the problem of efficient representation, manipulation, and communication of the numerical values in those computations arose. Strongly related to the problem of numerical representation is the problem of quantization: in what manner should a set of continuous real-valued numbers be distributed over a fixed discrete set of numbers to minimize the number of bits required and also to maximize the accuracy of the attendant computations? This perennial problem of quantization is particularly relevant whenever memory and/or computational resources are severely restricted, and it has come to the forefront in recent years due to the remarkable performance of Neural Network models in computer vision, natural language processing, and related areas. Moving from floating-point representations to low-precision fixed integer values represented in four bits or less holds the potential to reduce the memory footprint and latency by a factor of 16x; and, in fact, reductions of 4x to 8x are often realized in practice in these applications. Thus, it is not surprising that quantization has emerged recently as an important and very active sub-area of research in the efficient implementation of computations associated with Neural Networks. In this article, we survey approaches to the problem of quantizing the numerical values in deep Neural Network computations, covering the advantages/disadvantages of current methods. With this survey and its organization, we hope to have presented a useful snapshot of the current research in quantization for Neural Networks and to have given an intelligent organization to ease the evaluation of future research in this area.
Spectral clustering (SC) is a popular clustering technique to find strongly connected communities on a graph. SC can be used in Graph Neural Networks (GNNs) to implement pooling operations that aggregate nodes belonging to the same cluster. However, the eigendecomposition of the Laplacian is expensive and, since clustering results are graph-specific, pooling methods based on SC must perform a new optimization for each new sample. In this paper, we propose a graph clustering approach that addresses these limitations of SC. We formulate a continuous relaxation of the normalized minCUT problem and train a GNN to compute cluster assignments that minimize this objective. Our GNN-based implementation is differentiable, does not require to compute the spectral decomposition, and learns a clustering function that can be quickly evaluated on out-of-sample graphs. From the proposed clustering method, we design a graph pooling operator that overcomes some important limitations of state-of-the-art graph pooling techniques and achieves the best performance in several supervised and unsupervised tasks.