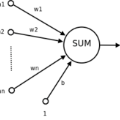
In the present paper, we consider one-hidden layer ANNs with a feedforward architecture, also referred to as shallow or two-layer networks, so that the structure is determined by the number and types of neurons. The determination of the parameters that define the function, called training, is done via the resolution of the approximation problem, so by imposing the interpolation through a set of specific nodes. We present the case where the parameters are trained using a procedure that is referred to as Extreme Learning Machine (ELM) that leads to a linear interpolation problem. In such hypotheses, the existence of an ANN interpolating function is guaranteed. The focus is then on the accuracy of the interpolation outside of the given sampling interpolation nodes when they are the equispaced, the Chebychev, and the randomly selected ones. The study is motivated by the well-known bell-shaped Runge example, which makes it clear that the construction of a global interpolating polynomial is accurate only if trained on suitably chosen nodes, ad example the Chebychev ones. In order to evaluate the behavior when growing the number of interpolation nodes, we raise the number of neurons in our network and compare it with the interpolating polynomial. We test using Runge's function and other well-known examples with different regularities. As expected, the accuracy of the approximation with a global polynomial increases only if the Chebychev nodes are considered. Instead, the error for the ANN interpolating function always decays and in most cases we observe that the convergence follows what is observed in the polynomial case on Chebychev nodes, despite the set of nodes used for training.
相關內容
In this paper, we present a learned and workload-aware variant of a Z-index, which jointly optimizes storage layout and search structures. Specifically, we first formulate a cost function to measure the performance of a Z-index on a dataset for a range-query workload. Then, we optimize the Z-index structure by minimizing the cost function through adaptive partitioning and ordering for index construction. Moreover, we design a novel page-skipping mechanism to improve its query performance by reducing access to irrelevant data pages. Our extensive experiments show that our index improves range query time by 40% on average over the baselines, while always performing better or comparably to state-of-the-art spatial indexes. Additionally, our index maintains good point query performance while providing favourable construction time and index size tradeoffs.
Permutation pattern-avoidance is a central concept of both enumerative and extremal combinatorics. In this paper we study the effect of permutation pattern-avoidance on the complexity of optimization problems. In the context of the dynamic optimality conjecture (Sleator, Tarjan, STOC 1983), Chalermsook, Goswami, Kozma, Mehlhorn, and Saranurak (FOCS 2015) conjectured that the amortized access cost of an optimal binary search tree (BST) is $O(1)$ whenever the access sequence avoids some fixed pattern. They showed a bound of $2^{\alpha{(n)}^{O(1)}}$, which was recently improved to $2^{\alpha{(n)}(1+o(1))}$ by Chalermsook, Pettie, and Yingchareonthawornchai (2023); here $n$ is the BST size and $\alpha(\cdot)$ the inverse-Ackermann function. In this paper we resolve the conjecture, showing a tight $O(1)$ bound. This indicates a barrier to dynamic optimality: any candidate online BST (e.g., splay trees or greedy trees) must match this optimum, but current analysis techniques only give superconstant bounds. More broadly, we argue that the easiness of pattern-avoiding input is a general phenomenon, not limited to BSTs or even to data structures. To illustrate this, we show that when the input avoids an arbitrary, fixed, a priori unknown pattern, one can efficiently compute a $k$-server solution of $n$ requests from a unit interval, with total cost $n^{O(1/\log k)}$, in contrast to the worst-case $\Theta(n/k)$ bound; and a traveling salesman tour of $n$ points from a unit box, of length $O(\log{n})$, in contrast to the worst-case $\Theta(\sqrt{n})$ bound; similar results hold for the euclidean minimum spanning tree, Steiner tree, and nearest-neighbor graphs. We show both results to be tight. Our techniques build on the Marcus-Tardos proof of the Stanley-Wilf conjecture, and on the recently emerging concept of twin-width; we believe our techniques to be more generally applicable.
This paper addresses the problem of designing the {\it continuous-discrete} unscented Kalman filter (UKF) implementation methods. More precisely, the aim is to propose the MATLAB-based UKF algorithms for {\it accurate} and {\it robust} state estimation of stochastic dynamic systems. The accuracy of the {\it continuous-discrete} nonlinear filters heavily depends on how the implementation method manages the discretization error arisen at the filter prediction step. We suggest the elegant and accurate implementation framework for tracking the hidden states by utilizing the MATLAB built-in numerical integration schemes developed for solving ordinary differential equations (ODEs). The accuracy is boosted by the discretization error control involved in all MATLAB ODE solvers. This keeps the discretization error below the tolerance value provided by users, automatically. Meanwhile, the robustness of the UKF filtering methods is examined in terms of the stability to roundoff. In contrast to the pseudo-square-root UKF implementations established in engineering literature, which are based on the one-rank Cholesky updates, we derive the stable square-root methods by utilizing the $J$-orthogonal transformations for calculating the Cholesky square-root factors.
A myriad of approaches have been proposed to characterise the mesoscale structure of networks - most often as a partition based on patterns variously called communities, blocks, or clusters. Clearly, distinct methods designed to detect different types of patterns may provide a variety of answers to the network's mesoscale structure. Yet, even multiple runs of a given method can sometimes yield diverse and conflicting results, producing entire landscapes of partitions which potentially include multiple (locally optimal) mesoscale explanations of the network. Such ambiguity motivates a closer look at the ability of these methods to find multiple qualitatively different 'ground truth' partitions in a network. Here, we propose the stochastic cross-block model (SCBM), a generative model which allows for two distinct partitions to be built into the mesoscale structure of a single benchmark network. We demonstrate a use case of the benchmark model by appraising the power of stochastic block models (SBMs) to detect implicitly planted coexisting bi-community and core-periphery structures of different strengths. Given our model design and experimental set-up, we find that the ability to detect the two partitions individually varies by SBM variant and that coexistence of both partitions is recovered only in a very limited number of cases. Our findings suggest that in most instances only one - in some way dominating - structure can be detected, even in the presence of other partitions. They underline the need for considering entire landscapes of partitions when different competing explanations exist and motivate future research to advance partition coexistence detection methods. Our model also contributes to the field of benchmark networks more generally by enabling further exploration of the ability of new and existing methods to detect ambiguity in the mesoscale structure of networks.
In this paper, we introduce a novel class of graphical models for representing time lag specific causal relationships and independencies of multivariate time series with unobserved confounders. We completely characterize these graphs and show that they constitute proper subsets of the currently employed model classes. As we show, from the novel graphs one can thus draw stronger causal inferences -- without additional assumptions. We further introduce a graphical representation of Markov equivalence classes of the novel graphs. This graphical representation contains more causal knowledge than what current state-of-the-art causal discovery algorithms learn.
As an optical processor, a Diffractive Deep Neural Network (D2NN) utilizes engineered diffractive surfaces designed through machine learning to perform all-optical information processing, completing its tasks at the speed of light propagation through thin optical layers. With sufficient degrees-of-freedom, D2NNs can perform arbitrary complex-valued linear transformations using spatially coherent light. Similarly, D2NNs can also perform arbitrary linear intensity transformations with spatially incoherent illumination; however, under spatially incoherent light, these transformations are non-negative, acting on diffraction-limited optical intensity patterns at the input field-of-view (FOV). Here, we expand the use of spatially incoherent D2NNs to complex-valued information processing for executing arbitrary complex-valued linear transformations using spatially incoherent light. Through simulations, we show that as the number of optimized diffractive features increases beyond a threshold dictated by the multiplication of the input and output space-bandwidth products, a spatially incoherent diffractive visual processor can approximate any complex-valued linear transformation and be used for all-optical image encryption using incoherent illumination. The findings are important for the all-optical processing of information under natural light using various forms of diffractive surface-based optical processors.
This paper presents a paraxial modeling approach for vibro-acoustography, a high-frequency ultrasound imaging technique that makes use of the excited low-frequency field to achieve a higher resolution while avoiding speckles. We start from a general second order wave equation, introduce a second order perturbation and make use of a paraxial change of variables to pass over to directed beams. Depending on the relation between the second order perturbation and the directivity of the beams this leads to different systems of PDEs that involve a spatially variable parameter governing the interaction of the incoming beams to generate the propagating acoustic field. We then consider the inverse problem of determining this parameter for one of these models where we present a Landweber-Kaczmarz reconstruction method to obtain a spatial image of the region of interest.
This paper develops a weak Galerkin (WG) finite element method of arbitrary order for the steady incompressible Magnetohydrodynamics equations. The WG scheme uses piecewise polynomials of degrees $k(k\geq 1),k,k-1$, and $k-1$ respectively for the approximations of the velocity, the magnetic field, the pressure, and the magnetic pseudo-pressure in the interior of elements, and uses piecewise polynomials of degree $k$ for their numerical traces on the interfaces of elements. The method is shown to yield globally divergence-free approximations of the velocity and magnetic fields. We give existence and uniqueness results for the discrete scheme and derive optimal a priori error estimates. We also present a convergent linearized iterative algorithm. Numerical experiments are provided to verify the obtained theoretical results.
In this paper we develop a novel neural network model for predicting implied volatility surface. Prior financial domain knowledge is taken into account. A new activation function that incorporates volatility smile is proposed, which is used for the hidden nodes that process the underlying asset price. In addition, financial conditions, such as the absence of arbitrage, the boundaries and the asymptotic slope, are embedded into the loss function. This is one of the very first studies which discuss a methodological framework that incorporates prior financial domain knowledge into neural network architecture design and model training. The proposed model outperforms the benchmarked models with the option data on the S&P 500 index over 20 years. More importantly, the domain knowledge is satisfied empirically, showing the model is consistent with the existing financial theories and conditions related to implied volatility surface.
This paper does not describe a working system. Instead, it presents a single idea about representation which allows advances made by several different groups to be combined into an imaginary system called GLOM. The advances include transformers, neural fields, contrastive representation learning, distillation and capsules. GLOM answers the question: How can a neural network with a fixed architecture parse an image into a part-whole hierarchy which has a different structure for each image? The idea is simply to use islands of identical vectors to represent the nodes in the parse tree. If GLOM can be made to work, it should significantly improve the interpretability of the representations produced by transformer-like systems when applied to vision or language