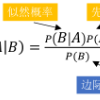
There are now many explainable AI methods for understanding the decisions of a machine learning model. Among these are those based on counterfactual reasoning, which involve simulating features changes and observing the impact on the prediction. This article proposes to view this simulation process as a source of creating a certain amount of knowledge that can be stored to be used, later, in different ways. This process is illustrated in the additive model and, more specifically, in the case of the naive Bayes classifier, whose interesting properties for this purpose are shown.
相關內容
Reinforcement learning is commonly concerned with problems of maximizing accumulated rewards in Markov decision processes. Oftentimes, a certain goal state or a subset of the state space attain maximal reward. In such a case, the environment may be considered solved when the goal is reached. Whereas numerous techniques, learning or non-learning based, exist for solving environments, doing so optimally is the biggest challenge. Say, one may choose a reward rate which penalizes the action effort. Reinforcement learning is currently among the most actively developed frameworks for solving environments optimally by virtue of maximizing accumulated reward, in other words, returns. Yet, tuning agents is a notoriously hard task as reported in a series of works. Our aim here is to help the agent learn a near-optimal policy efficiently while ensuring a goal reaching property of some basis policy that merely solves the environment. We suggest an algorithm, which is fairly flexible, and can be used to augment practically any agent as long as it comprises of a critic. A formal proof of a goal reaching property is provided. Simulation experiments on six problems under five agents, including the benchmarked one, provided an empirical evidence that the learning can indeed be boosted while ensuring goal reaching property.
Computability on uncountable sets has no standard formalization, unlike that on countable sets, which is given by Turing machines. Some of the approaches to define computability in these sets rely on order-theoretic structures to translate such notions from Turing machines to uncountable spaces. Since these machines are used as a baseline for computability in these approaches, countability restrictions on the ordered structures are fundamental. Here, we show several relations between the usual countability restrictions in order-theoretic theories of computability and some more common order-theoretic countability constraints, like order density properties and functional characterizations of the order structure in terms of multi-utilities. As a result, we show how computability can be introduced in some order structures via countability order density and multi-utility constraints.
Regression methods dominate the practice of biostatistical analysis, but biostatistical training emphasises the details of regression models and methods ahead of the purposes for which such modelling might be useful. More broadly, statistics is widely understood to provide a body of techniques for "modelling data", underpinned by what we describe as the "true model myth": that the task of the statistician/data analyst is to build a model that closely approximates the true data generating process. By way of our own historical examples and a brief review of mainstream clinical research journals, we describe how this perspective has led to a range of problems in the application of regression methods, including misguided "adjustment" for covariates, misinterpretation of regression coefficients and the widespread fitting of regression models without a clear purpose. We then outline a new approach to the teaching and application of biostatistical methods, which situates them within a framework that first requires clear definition of the substantive research question at hand within one of three categories: descriptive, predictive, or causal. Within this approach, the simple univariable regression model may be introduced as a tool for description, while the development and application of multivariable regression models as well as other advanced biostatistical methods should proceed differently according to the type of question. Regression methods will no doubt remain central to statistical practice as they provide a powerful tool for representing variation in a response or outcome variable as a function of "input" variables, but their conceptualisation and usage should follow from the purpose at hand.
Ising machines are dedicated hardware solvers of NP-hard optimization problems. However, they do not always find the most optimal solution. The probability of finding this optimal solution depends on the problem at hand. Using continuation methods, we show that this is closely linked to the bifurcation sequence of the optimal solution. From this bifurcation analysis, we can determine the effectiveness of solution schemes. Moreover, we find that the proper choice of implementation of the Ising machine can drastically change this bifurcation sequence and therefore vastly increase the probability of finding the optimal solution.
Advanced artificial intelligence (AI) systems with access to millions of research papers could inspire new research ideas that may not be conceived by humans alone. However, how interesting are these AI-generated ideas, and how can we improve their quality? Here, we introduce SciMuse, a system that uses an evolving knowledge graph built from more than 58 million scientific papers to generate personalized research ideas via an interface to GPT-4. We conducted a large-scale human evaluation with over 100 research group leaders from the Max Planck Society, who ranked more than 4,000 personalized research ideas based on their level of interest. This evaluation allows us to understand the relationships between scientific interest and the core properties of the knowledge graph. We find that data-efficient machine learning can predict research interest with high precision, allowing us to optimize the interest-level of generated research ideas. This work represents a step towards an artificial scientific muse that could catalyze unforeseen collaborations and suggest interesting avenues for scientists.
This paper proposes two innovative vector transport operators, leveraging the Cayley transform, for the generalized Stiefel manifold embedded with a non-standard metric. Specifically, it introduces the differentiated retraction and an approximation of the Cayley transform to the differentiated matrix exponential. These vector transports are demonstrated to satisfy the Ring-Wirth non-expansive condition under non-standard metrics, and one of them is also isometric. Building upon the novel vector transport operators, we extend the modified Polak-Ribi$\grave{e}$re-Polyak (PRP) conjugate gradient method to the generalized Stiefel manifold. Under a non-monotone line search condition, we prove our algorithm globally converges to a stationary point. The efficiency of the proposed vector transport operators is empirically validated through numerical experiments involving generalized eigenvalue problems and canonical correlation analysis.
Through an uncertainty quantification (UQ) perspective, we show that score-based generative models (SGMs) are provably robust to the multiple sources of error in practical implementation. Our primary tool is the Wasserstein uncertainty propagation (WUP) theorem, a model-form UQ bound that describes how the $L^2$ error from learning the score function propagates to a Wasserstein-1 ($\mathbf{d}_1$) ball around the true data distribution under the evolution of the Fokker-Planck equation. We show how errors due to (a) finite sample approximation, (b) early stopping, (c) score-matching objective choice, (d) score function parametrization expressiveness, and (e) reference distribution choice, impact the quality of the generative model in terms of a $\mathbf{d}_1$ bound of computable quantities. The WUP theorem relies on Bernstein estimates for Hamilton-Jacobi-Bellman partial differential equations (PDE) and the regularizing properties of diffusion processes. Specifically, PDE regularity theory shows that stochasticity is the key mechanism ensuring SGM algorithms are provably robust. The WUP theorem applies to integral probability metrics beyond $\mathbf{d}_1$, such as the total variation distance and the maximum mean discrepancy. Sample complexity and generalization bounds in $\mathbf{d}_1$ follow directly from the WUP theorem. Our approach requires minimal assumptions, is agnostic to the manifold hypothesis and avoids absolute continuity assumptions for the target distribution. Additionally, our results clarify the trade-offs among multiple error sources in SGMs.
Partial multi-task learning where training examples are annotated for one of the target tasks is a promising idea in remote sensing as it allows combining datasets annotated for different tasks and predicting more tasks with fewer network parameters. The na\"ive approach to partial multi-task learning is sub-optimal due to the lack of all-task annotations for learning joint representations. This paper proposes using knowledge distillation to replace the need of ground truths for the alternate task and enhance the performance of such approach. Experiments conducted on the public ISPRS 2D Semantic Labeling Contest dataset show the effectiveness of the proposed idea on partial multi-task learning for semantic tasks including object detection and semantic segmentation in aerial images.
Since the weak convergence for stochastic processes does not account for the growth of information over time which is represented by the underlying filtration, a slightly erroneous stochastic model in weak topology may cause huge loss in multi-periods decision making problems. To address such discontinuities Aldous introduced the extended weak convergence, which can fully characterise all essential properties, including the filtration, of stochastic processes; however was considered to be hard to find efficient numerical implementations. In this paper, we introduce a novel metric called High Rank PCF Distance (HRPCFD) for extended weak convergence based on the high rank path development method from rough path theory, which also defines the characteristic function for measure-valued processes. We then show that such HRPCFD admits many favourable analytic properties which allows us to design an efficient algorithm for training HRPCFD from data and construct the HRPCF-GAN by using HRPCFD as the discriminator for conditional time series generation. Our numerical experiments on both hypothesis testing and generative modelling validate the out-performance of our approach compared with several state-of-the-art methods, highlighting its potential in broad applications of synthetic time series generation and in addressing classic financial and economic challenges, such as optimal stopping or utility maximisation problems.
Incorporating prior knowledge into pre-trained language models has proven to be effective for knowledge-driven NLP tasks, such as entity typing and relation extraction. Current pre-training procedures usually inject external knowledge into models by using knowledge masking, knowledge fusion and knowledge replacement. However, factual information contained in the input sentences have not been fully mined, and the external knowledge for injecting have not been strictly checked. As a result, the context information cannot be fully exploited and extra noise will be introduced or the amount of knowledge injected is limited. To address these issues, we propose MLRIP, which modifies the knowledge masking strategies proposed by ERNIE-Baidu, and introduce a two-stage entity replacement strategy. Extensive experiments with comprehensive analyses illustrate the superiority of MLRIP over BERT-based models in military knowledge-driven NLP tasks.