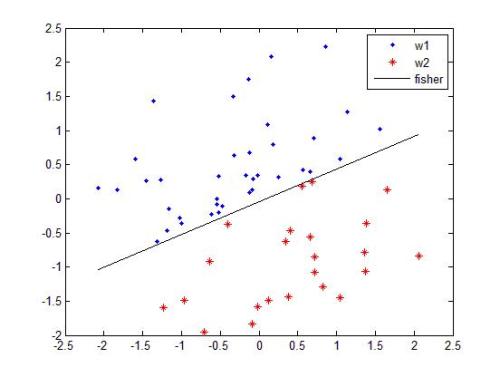
Support vector machines (SVM) and other kernel techniques represent a family of powerful statistical classification methods with high accuracy and broad applicability. Because they use all or a significant portion of the training data, however, they can be slow, especially for large problems. Piecewise linear classifiers are similarly versatile, yet have the additional advantages of simplicity, ease of interpretation and, if the number of component linear classifiers is not too large, speed. Here we show how a simple, piecewise linear classifier can be trained from a kernel-based classifier in order to improve the classification speed. The method works by finding the root of the difference in conditional probabilities between pairs of opposite classes to build up a representation of the decision boundary. When tested on 17 different datasets, it succeeded in improving the classification speed of a SVM for 12 of them by up to two orders-of-magnitude. Of these, two were less accurate than a simple, linear classifier. The method is best suited to problems with continuum features data and smooth probability functions. Because the component linear classifiers are built up individually from an existing classifier, rather than through a simultaneous optimization procedure, the classifier is also fast to train.
相關內容
In applications of group testing in networks, e.g. identifying individuals who are infected by a disease spread over a network, exploiting correlation among network nodes provides fundamental opportunities in reducing the number of tests needed. We model and analyze group testing on $n$ correlated nodes whose interactions are specified by a graph $G$. We model correlation through an edge-faulty random graph formed from $G$ in which each edge is dropped with probability $1-r$, and all nodes in the same component have the same state. We consider three classes of graphs: cycles and trees, $d$-regular graphs and stochastic block models or SBM, and obtain lower and upper bounds on the number of tests needed to identify the defective nodes. Our results are expressed in terms of the number of tests needed when the nodes are independent and they are in terms of $n$, $r$, and the target error. In particular, we quantify the fundamental improvements that exploiting correlation offers by the ratio between the total number of nodes $n$ and the equivalent number of independent nodes in a classic group testing algorithm. The lower bounds are derived by illustrating a strong dependence of the number of tests needed on the expected number of components. In this regard, we establish a new approximation for the distribution of component sizes in "$d$-regular trees" which may be of independent interest and leads to a lower bound on the expected number of components in $d$-regular graphs. The upper bounds are found by forming dense subgraphs in which nodes are more likely to be in the same state. When $G$ is a cycle or tree, we show an improvement by a factor of $log(1/r)$. For grid, a graph with almost $2n$ edges, the improvement is by a factor of ${(1-r) \log(1/r)}$, indicating drastic improvement compared to trees. When $G$ has a larger number of edges, as in SBM, the improvement can scale in $n$.
It is a common phenomenon that for high-dimensional and nonparametric statistical models, rate-optimal estimators balance squared bias and variance. Although this balancing is widely observed, little is known whether methods exist that could avoid the trade-off between bias and variance. We propose a general strategy to obtain lower bounds on the variance of any estimator with bias smaller than a prespecified bound. This shows to which extent the bias-variance trade-off is unavoidable and allows to quantify the loss of performance for methods that do not obey it. The approach is based on a number of abstract lower bounds for the variance involving the change of expectation with respect to different probability measures as well as information measures such as the Kullback-Leibler or $\chi^2$-divergence. In a second part of the article, the abstract lower bounds are applied to several statistical models including the Gaussian white noise model, a boundary estimation problem, the Gaussian sequence model and the high-dimensional linear regression model. For these specific statistical applications, different types of bias-variance trade-offs occur that vary considerably in their strength. For the trade-off between integrated squared bias and integrated variance in the Gaussian white noise model, we propose to combine the general strategy for lower bounds with a reduction technique. This allows us to reduce the original problem to a lower bound on the bias-variance trade-off for estimators with additional symmetry properties in a simpler statistical model. In the Gaussian sequence model, different phase transitions of the bias-variance trade-off occur. Although there is a non-trivial interplay between bias and variance, the rate of the squared bias and the variance do not have to be balanced in order to achieve the minimax estimation rate.
Classification and segmentation are crucial in medical image analysis as they enable accurate diagnosis and disease monitoring. However, current methods often prioritize the mutual learning features and shared model parameters, while neglecting the reliability of features and performances. In this paper, we propose a novel Uncertainty-informed Mutual Learning (UML) framework for reliable and interpretable medical image analysis. Our UML introduces reliability to joint classification and segmentation tasks, leveraging mutual learning with uncertainty to improve performance. To achieve this, we first use evidential deep learning to provide image-level and pixel-wise confidences. Then, an Uncertainty Navigator Decoder is constructed for better using mutual features and generating segmentation results. Besides, an Uncertainty Instructor is proposed to screen reliable masks for classification. Overall, UML could produce confidence estimation in features and performance for each link (classification and segmentation). The experiments on the public datasets demonstrate that our UML outperforms existing methods in terms of both accuracy and robustness. Our UML has the potential to explore the development of more reliable and explainable medical image analysis models. We will release the codes for reproduction after acceptance.
We consider optimal intervention in the Elliott-Golub-Jackson network model \cite{jackson14} and we show that it can be transformed into an influence maximization-like form, interpreted as the reverse of a default cascade. Our analysis of the optimal intervention problem extends well-established targeting results to the economic network setting, which requires additional theoretical steps. We prove several results about optimal intervention: it is NP-hard and cannot be approximated to a constant factor in polynomial time. In turn, we show that randomizing failure thresholds leads to a version of the problem which is monotone submodular, for which existing powerful approximations in polynomial time can be applied. In addition to optimal intervention, we also show practical consequences of our analysis to other economic network problems: (1) it is computationally hard to calculate expected values in the economic network, and (2) influence maximization algorithms can enable efficient importance sampling and stress testing of large failure scenarios. We illustrate our results on a network of firms connected through input-output linkages inferred from the World Input Output Database.
Fine-tuning large pre-trained language models on downstream tasks has become an important paradigm in NLP. However, common practice fine-tunes all of the parameters in a pre-trained model, which becomes prohibitive when a large number of downstream tasks are present. Therefore, many fine-tuning methods are proposed to learn incremental updates of pre-trained weights in a parameter efficient way, e.g., low-rank increments. These methods often evenly distribute the budget of incremental updates across all pre-trained weight matrices, and overlook the varying importance of different weight parameters. As a consequence, the fine-tuning performance is suboptimal. To bridge this gap, we propose AdaLoRA, which adaptively allocates the parameter budget among weight matrices according to their importance score. In particular, AdaLoRA parameterizes the incremental updates in the form of singular value decomposition. Such a novel approach allows us to effectively prune the singular values of unimportant updates, which is essentially to reduce their parameter budget but circumvent intensive exact SVD computations. We conduct extensive experiments with several pre-trained models on natural language processing, question answering, and natural language generation to validate the effectiveness of AdaLoRA. Results demonstrate that AdaLoRA manifests notable improvement over baselines, especially in the low budget settings. Our code is publicly available at //github.com/QingruZhang/AdaLoRA .
The coresets approach, also called subsampling or subset selection, aims to select a subsample as a surrogate for the observed sample. Such an approach has been used pervasively in large-scale data analysis. Existing coresets methods construct the subsample using a subset of rows from the predictor matrix. Such methods can be significantly inefficient when the predictor matrix is sparse or numerically sparse. To overcome the limitation, we develop a novel element-wise subset selection approach, called core-elements, for large-scale least squares estimation in classical linear regression. We provide a deterministic algorithm to construct the core-elements estimator, only requiring an $O(\mbox{nnz}(\mathbf{X})+rp^2)$ computational cost, where $\mathbf{X}$ is an $n\times p$ predictor matrix, $r$ is the number of elements selected from each column of $\mathbf{X}$, and $\mbox{nnz}(\cdot)$ denotes the number of non-zero elements. Theoretically, we show that the proposed estimator is unbiased and approximately minimizes an upper bound of the estimation variance. We also provide an approximation guarantee by deriving a coresets-like finite sample bound for the proposed estimator. To handle potential outliers in the data, we further combine core-elements with the median-of-means procedure, resulting in an efficient and robust estimator with theoretical consistency guarantees. Numerical studies on various synthetic and open-source datasets demonstrate the proposed method's superior performance compared to mainstream competitors.
We study the problem of verification and synthesis of robust control barrier functions (CBF) for control-affine polynomial systems with bounded additive uncertainty and convex polynomial constraints on the control. We first formulate robust CBF verification and synthesis as multilevel polynomial optimization problems (POP), where verification optimizes -- in three levels -- the uncertainty, control, and state, while synthesis additionally optimizes the parameter of a chosen parametric CBF candidate. We then show that, by invoking the KKT conditions of the inner optimizations over uncertainty and control, the verification problem can be simplified as a single-level POP and the synthesis problem reduces to a min-max POP. This reduction leads to multilevel semidefinite relaxations. For the verification problem, we apply Lasserre's hierarchy of moment relaxations. For the synthesis problem, we draw connections to existing relaxation techniques for robust min-max POP, which first use sum-of-squares programming to find increasingly tight polynomial lower bounds to the unknown value function of the verification POP, and then call Lasserre's hierarchy again to maximize the lower bounds. Both semidefinite relaxations guarantee asymptotic global convergence to optimality. We provide an in-depth study of our framework on the controlled Van der Pol Oscillator, both with and without additive uncertainty.
Class incremental learning (CIL) is the process of continually learning new object classes from incremental data while not forgetting past learned classes. While the common method for evaluating CIL algorithms is based on average test accuracy for all learned classes, we argue that maximizing accuracy alone does not necessarily lead to effective CIL algorithms. In this paper, we experimentally analyze neural network models trained by CIL algorithms using various evaluation protocols in representation learning and propose a new analysis method. Our experiments show that most state-of-the-art algorithms prioritize high stability and do not significantly change the learned representation, and sometimes even learn a representation of lower quality than a naive baseline. However, we observe that these algorithms can still achieve high test accuracy because they learn a classifier that is closer to the optimal classifier. We also found that the base model learned in the first task varies in representation quality across different algorithms, and changes in the final performance were observed when each algorithm was trained under similar representation quality of the base model. Thus, we suggest that representation-level evaluation is an additional recipe for more objective evaluation and effective development of CIL algorithms.
The performance of a Collaborative Filtering (CF) method is based on the properties of a User-Item Rating Matrix (URM). And the properties or Rating Data Characteristics (RDC) of a URM are constantly changing. Recent studies significantly explained the variation in the performances of CF methods resulted due to the change in URM using six or more RDC. Here, we found that the significant proportion of variation in the performances of different CF techniques can be accounted to two RDC only. The two RDC are the number of ratings per user or Information per User (IpU) and the number of ratings per item or Information per Item (IpI). And the performances of CF algorithms are quadratic to IpU (or IpI) for a square URM. The findings of this study are based on seven well-established CF methods and three popular public recommender datasets: 1M MovieLens, 25M MovieLens, and Yahoo! Music Rating datasets
Graph Convolutional Networks (GCNs) have been widely applied in various fields due to their significant power on processing graph-structured data. Typical GCN and its variants work under a homophily assumption (i.e., nodes with same class are prone to connect to each other), while ignoring the heterophily which exists in many real-world networks (i.e., nodes with different classes tend to form edges). Existing methods deal with heterophily by mainly aggregating higher-order neighborhoods or combing the immediate representations, which leads to noise and irrelevant information in the result. But these methods did not change the propagation mechanism which works under homophily assumption (that is a fundamental part of GCNs). This makes it difficult to distinguish the representation of nodes from different classes. To address this problem, in this paper we design a novel propagation mechanism, which can automatically change the propagation and aggregation process according to homophily or heterophily between node pairs. To adaptively learn the propagation process, we introduce two measurements of homophily degree between node pairs, which is learned based on topological and attribute information, respectively. Then we incorporate the learnable homophily degree into the graph convolution framework, which is trained in an end-to-end schema, enabling it to go beyond the assumption of homophily. More importantly, we theoretically prove that our model can constrain the similarity of representations between nodes according to their homophily degree. Experiments on seven real-world datasets demonstrate that this new approach outperforms the state-of-the-art methods under heterophily or low homophily, and gains competitive performance under homophily.