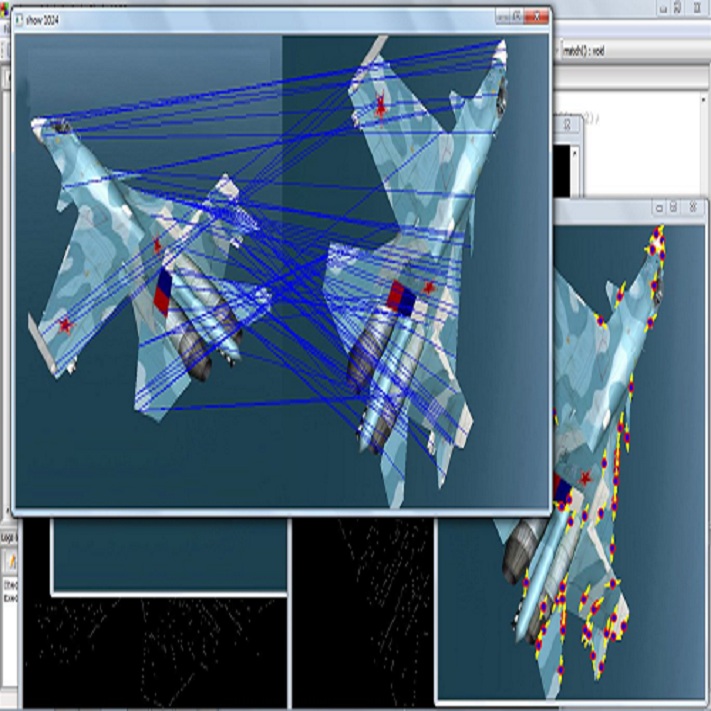
The correlation of optical measurements with a correct pathology label is often hampered by imprecise registration caused by deformations in histology images. This study explores an automated multi-modal image registration technique utilizing deep learning principles to align snapshot breast specimen images with corresponding histology images. The input images, acquired through different modalities, present challenges due to variations in intensities and structural visibility, making linear assumptions inappropriate. An unsupervised and supervised learning approach, based on the VoxelMorph model, was explored, making use of a dataset with manually registered images used as ground truth. Evaluation metrics, including Dice scores and mutual information, reveal that the unsupervised model outperforms the supervised (and manual approach) significantly, achieving superior image alignment. This automated registration approach holds promise for improving the validation of optical technologies by minimizing human errors and inconsistencies associated with manual registration.
相關內容
The optimal one-sided parametric polynomial approximants of a circular arc are considered. More precisely, the approximant must be entirely in or out of the underlying circle of an arc. The natural restriction to an arc's approximants interpolating boundary points is assumed. However, the study of approximants, which additionally interpolate corresponding tangent directions and curvatures at the boundary of an arc, is also considered. Several low-degree polynomial approximants are studied in detail. When several solutions fulfilling the interpolation conditions exist, the optimal one is characterized, and a numerical algorithm for its construction is suggested. Theoretical results are demonstrated with several numerical examples and a comparison with general (i.e. non-one-sided) approximants are provided.
Membrane systems are a biologically-inspired computational model based on the structure of biological cells and the way chemicals interact and traverse their membranes. Although their dynamics are described by rules, encoding membrane systems into rewriting logic is not straightforward due to its complex control mechanisms. Multiple alternatives have been proposed in the literature and implemented in the Maude specification language. The recent release of the Maude strategy language and its associated strategy-aware model checker allow specifying these systems more easily, so that they become executable and verifiable for free. An easily-extensible interactive environment transforms membrane specifications into rewrite theories controlled by appropriate strategies, and allows simulating and verifying membrane computations by means of them.
With insurers benefiting from ever-larger amounts of data of increasing complexity, we explore a data-driven method to model dependence within multilevel claims in this paper. More specifically, we start from a non-parametric estimator for Archimedean copula generators introduced by Genest and Rivest (1993), and we extend it to diverse flexible censoring scenarios using techniques derived from survival analysis. We implement a graphical selection procedure for copulas that we validate using goodness-of-fit methods applied to complete, single-censored, and double-censored bivariate data. We illustrate the performance of our model with multiple simulation studies. We then apply our methodology to a recent Canadian automobile insurance dataset where we seek to model the dependence between the activation delays of correlated coverages. We show that our model performs quite well in selecting the best-fitted copula for the data at hand, especially when the dataset is large, and that the results can then be used as part of a larger claims reserving methodology.
For obtaining optimal first-order convergence guarantee for stochastic optimization, it is necessary to use a recurrent data sampling algorithm that samples every data point with sufficient frequency. Most commonly used data sampling algorithms (e.g., i.i.d., MCMC, random reshuffling) are indeed recurrent under mild assumptions. In this work, we show that for a particular class of stochastic optimization algorithms, we do not need any other property (e.g., independence, exponential mixing, and reshuffling) than recurrence in data sampling algorithms to guarantee the optimal rate of first-order convergence. Namely, using regularized versions of Minimization by Incremental Surrogate Optimization (MISO), we show that for non-convex and possibly non-smooth objective functions, the expected optimality gap converges at an optimal rate $O(n^{-1/2})$ under general recurrent sampling schemes. Furthermore, the implied constant depends explicitly on the `speed of recurrence', measured by the expected amount of time to visit a given data point either averaged (`target time') or supremized (`hitting time') over the current location. We demonstrate theoretically and empirically that convergence can be accelerated by selecting sampling algorithms that cover the data set most effectively. We discuss applications of our general framework to decentralized optimization and distributed non-negative matrix factorization.
In a network of reinforced stochastic processes, for certain values of the parameters, all the agents' inclinations synchronize and converge almost surely toward a certain random variable. The present work aims at clarifying when the agents can asymptotically polarize, i.e. when the common limit inclination can take the extreme values, 0 or 1, with probability zero, strictly positive, or equal to one. Moreover, we present a suitable technique to estimate this probability that, along with the theoretical results, has been framed in the more general setting of a class of martingales taking values in [0, 1] and following a specific dynamics.
We investigate distributional properties of a class of spectral spatial statistics under irregular sampling of a random field that is defined on $\mathbb{R}^d$, and use this to obtain a test for isotropy. Within this context, edge effects are well-known to create a bias in classical estimators commonly encountered in the analysis of spatial data. This bias increases with dimension $d$ and, for $d>1$, can become non-negligible in the limiting distribution of such statistics to the extent that a nondegenerate distribution does not exist. We provide a general theory for a class of (integrated) spectral statistics that enables to 1) significantly reduce this bias and 2) that ensures that asymptotically Gaussian limits can be derived for $d \le 3$ for appropriately tapered versions of such statistics. We use this to address some crucial gaps in the literature, and demonstrate that tapering with a sufficiently smooth function is necessary to achieve such results. Our findings specifically shed a new light on a recent result in Subba Rao (2018a). Our theory then is used to propose a novel test for isotropy. In contrast to most of the literature, which validates this assumption on a finite number of spatial locations (or a finite number of Fourier frequencies), we develop a test for isotropy on the full spatial domain by means of its characterization in the frequency domain. More precisely, we derive an explicit expression for the minimum $L^2$-distance between the spectral density of the random field and its best approximation by a spectral density of an isotropic process. We prove asymptotic normality of an estimator of this quantity in the mixed increasing domain framework and use this result to derive an asymptotic level $\alpha$-test.

We characterize structures such as monotonicity, convexity, and modality in smooth regression curves using persistent homology. Persistent homology is a key tool in topological data analysis that detects higher dimensional topological features such as connected components and holes (cycles or loops) in the data. In other words, persistent homology is a multiscale version of homology that characterizes sets based on the connected components and holes. We use super-level sets of functions to extract geometric features via persistent homology. In particular, we explore structures in regression curves via the persistent homology of super-level sets of a function, where the function of interest is - the first derivative of the regression function. In the course of this study, we extend an existing procedure of estimating the persistent homology for the first derivative of a regression function and establish its consistency. Moreover, as an application of the proposed methodology, we demonstrate that the persistent homology of the derivative of a function can reveal hidden structures in the function that are not visible from the persistent homology of the function itself. In addition, we also illustrate that the proposed procedure can be used to compare the shapes of two or more regression curves which is not possible merely from the persistent homology of the function itself.
Fully understanding a complex high-resolution satellite or aerial imagery scene often requires spatial reasoning over a broad relevant context. The human object recognition system is able to understand object in a scene over a long-range relevant context. For example, if a human observes an aerial scene that shows sections of road broken up by tree canopy, then they will be unlikely to conclude that the road has actually been broken up into disjoint pieces by trees and instead think that the canopy of nearby trees is occluding the road. However, there is limited research being conducted to understand long-range context understanding of modern machine learning models. In this work we propose a road segmentation benchmark dataset, Chesapeake Roads Spatial Context (RSC), for evaluating the spatial long-range context understanding of geospatial machine learning models and show how commonly used semantic segmentation models can fail at this task. For example, we show that a U-Net trained to segment roads from background in aerial imagery achieves an 84% recall on unoccluded roads, but just 63.5% recall on roads covered by tree canopy despite being trained to model both the same way. We further analyze how the performance of models changes as the relevant context for a decision (unoccluded roads in our case) varies in distance. We release the code to reproduce our experiments and dataset of imagery and masks to encourage future research in this direction -- //github.com/isaaccorley/ChesapeakeRSC.
Savje (2023) recommends misspecified exposure effects as a way to avoid strong assumptions about interference when analyzing the results of an experiment. In this discussion, we highlight a key limitation of Savje's recommendation. Exposure effects are not generally useful for evaluating social policies without the strong assumptions that Savje seeks to avoid. Our discussion is organized as follows. Section 2 summarizes our position, section 3 provides a concrete example, and section 4 concludes. Proof of claims are in an appendix.
Hashing has been widely used in approximate nearest search for large-scale database retrieval for its computation and storage efficiency. Deep hashing, which devises convolutional neural network architecture to exploit and extract the semantic information or feature of images, has received increasing attention recently. In this survey, several deep supervised hashing methods for image retrieval are evaluated and I conclude three main different directions for deep supervised hashing methods. Several comments are made at the end. Moreover, to break through the bottleneck of the existing hashing methods, I propose a Shadow Recurrent Hashing(SRH) method as a try. Specifically, I devise a CNN architecture to extract the semantic features of images and design a loss function to encourage similar images projected close. To this end, I propose a concept: shadow of the CNN output. During optimization process, the CNN output and its shadow are guiding each other so as to achieve the optimal solution as much as possible. Several experiments on dataset CIFAR-10 show the satisfying performance of SRH.