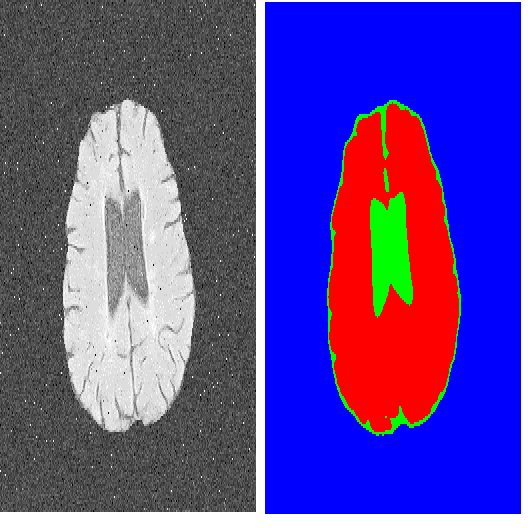
In this paper, we propose a multi-stage image segmentation framework that incorporates a weighted difference of anisotropic and isotropic total variation (AITV). The segmentation framework generally consists of two stages: smoothing and thresholding, thus referred to as SaT. In the first stage, a smoothed image is obtained by an AITV-regularized Mumford-Shah (MS) model, which can be solved efficiently by the alternating direction method of multipliers (ADMM) with a closed-form solution of a proximal operator of the $\ell_1 -\alpha \ell_2$ regularizer. Convergence of the ADMM algorithm is analyzed. In the second stage, we threshold the smoothed image by $k$-means clustering to obtain the final segmentation result. Numerical experiments demonstrate that the proposed segmentation framework is versatile for both grayscale and color images, efficient in producing high-quality segmentation results within a few seconds, and robust to input images that are corrupted with noise, blur, or both. We compare the AITV method with its original convex and nonconvex TV$^p (0<p<1)$ counterparts, showcasing the qualitative and quantitative advantages of our proposed method.
相關內容
This paper revisits the problem of sampling and transmitting status updates through a channel with random delay under a sampling frequency constraint \cite{sun_17_tit}. We use the Age of Information (AoI) to characterize the status information freshness at the receiver. The goal is to design a sampling policy that can minimize the average AoI when the statistics of delay is unknown. We reformulate the problem as the optimization of a renewal-reward process, and propose an online sampling strategy based on the Robbins-Monro algorithm. We prove that the proposed algorithm satisfies the sampling frequency constraint. Moreover, when the transmission delay is bounded and its distribution is absolutely continuous, the average AoI obtained by the proposed algorithm converges to the minimum AoI when the number of samples $K$ goes to infinity with probability 1. We show that the optimality gap decays with rate $\mathcal{O}\left(\ln K/K\right)$, and the proposed algorithm is minimax rate optimal. Simulation results validate the performance of our proposed algorithm.
Removing noise from the any processed images is very important. Noise should be removed in such a way that important information of image should be preserved. A decisionbased nonlinear algorithm for elimination of band lines, drop lines, mark, band lost and impulses in images is presented in this paper. The algorithm performs two simultaneous operations, namely, detection of corrupted pixels and evaluation of new pixels for replacing the corrupted pixels. Removal of these artifacts is achieved without damaging edges and details. However, the restricted window size renders median operation less effective whenever noise is excessive in that case the proposed algorithm automatically switches to mean filtering. The performance of the algorithm is analyzed in terms of Mean Square Error [MSE], Peak-Signal-to-Noise Ratio [PSNR], Signal-to-Noise Ratio Improved [SNRI], Percentage Of Noise Attenuated [PONA], and Percentage Of Spoiled Pixels [POSP]. This is compared with standard algorithms already in use and improved performance of the proposed algorithm is presented. The advantage of the proposed algorithm is that a single algorithm can replace several independent algorithms which are required for removal of different artifacts.
The hard thresholding technique plays a vital role in the development of algorithms for sparse signal recovery. By merging this technique and heavy-ball acceleration method which is a multi-step extension of the traditional gradient descent method, we propose the so-called heavy-ball-based hard thresholding (HBHT) and heavy-ball-based hard thresholding pursuit (HBHTP) algorithms for signal recovery. It turns out that the HBHT and HBHTP can successfully recover a $k$-sparse signal if the restricted isometry constant of the measurement matrix satisfies $\delta_{3k}<0.618 $ and $\delta_{3k}<0.577,$ respectively. The guaranteed success of HBHT and HBHTP is also shown under the conditions $\delta_{2k}<0.356$ and $\delta_{2k}<0.377,$ respectively. Moreover, the finite convergence and stability of the two algorithms are also established in this paper. Simulations on random problem instances are performed to compare the performance of the proposed algorithms and several existing ones. Empirical results indicate that the HBHTP performs very comparably to a few existing algorithms and it takes less average time to achieve the signal recovery than these existing methods.
The Mixture-of-Experts (MoE) technique can scale up the model size of Transformers with an affordable computational overhead. We point out that existing learning-to-route MoE methods suffer from the routing fluctuation issue, i.e., the target expert of the same input may change along with training, but only one expert will be activated for the input during inference. The routing fluctuation tends to harm sample efficiency because the same input updates different experts but only one is finally used. In this paper, we propose StableMoE with two training stages to address the routing fluctuation problem. In the first training stage, we learn a balanced and cohesive routing strategy and distill it into a lightweight router decoupled from the backbone model. In the second training stage, we utilize the distilled router to determine the token-to-expert assignment and freeze it for a stable routing strategy. We validate our method on language modeling and multilingual machine translation. The results show that StableMoE outperforms existing MoE methods in terms of both convergence speed and performance.
In this paper we study the finite sample and asymptotic properties of various weighting estimators of the local average treatment effect (LATE), several of which are based on Abadie (2003)'s kappa theorem. Our framework presumes a binary endogenous explanatory variable ("treatment") and a binary instrumental variable, which may only be valid after conditioning on additional covariates. We argue that one of the Abadie estimators, which we show is weight normalized, is likely to dominate the others in many contexts. A notable exception is in settings with one-sided noncompliance, where certain unnormalized estimators have the advantage of being based on a denominator that is bounded away from zero. We use a simulation study and three empirical applications to illustrate our findings. In applications to causal effects of college education using the college proximity instrument (Card, 1995) and causal effects of childbearing using the sibling sex composition instrument (Angrist and Evans, 1998), the unnormalized estimates are clearly unreasonable, with "incorrect" signs, magnitudes, or both. Overall, our results suggest that (i) the relative performance of different kappa weighting estimators varies with features of the data-generating process; and that (ii) the normalized version of Tan (2006)'s estimator may be an attractive alternative in many contexts. Applied researchers with access to a binary instrumental variable should also consider covariate balancing or doubly robust estimators of the LATE.
We propose a simple modification to the iterative hard thresholding (IHT) algorithm, which recovers asymptotically sparser solutions as a function of the condition number. When aiming to minimize a convex function $f(x)$ with condition number $\kappa$ subject to $x$ being an $s$-sparse vector, the standard IHT guarantee is a solution with relaxed sparsity $O(s\kappa^2)$, while our proposed algorithm, regularized IHT, returns a solution with sparsity $O(s\kappa)$. Our algorithm significantly improves over ARHT which also finds a solution of sparsity $O(s\kappa)$, as it does not require re-optimization in each iteration (and so is much faster), is deterministic, and does not require knowledge of the optimal solution value $f(x^*)$ or the optimal sparsity level $s$. Our main technical tool is an adaptive regularization framework, in which the algorithm progressively learns the weights of an $\ell_2$ regularization term that will allow convergence to sparser solutions. We also apply this framework to low rank optimization, where we achieve a similar improvement of the best known condition number dependence from $\kappa^2$ to $\kappa$.
The U-Net was presented in 2015. With its straight-forward and successful architecture it quickly evolved to a commonly used benchmark in medical image segmentation. The adaptation of the U-Net to novel problems, however, comprises several degrees of freedom regarding the exact architecture, preprocessing, training and inference. These choices are not independent of each other and substantially impact the overall performance. The present paper introduces the nnU-Net ('no-new-Net'), which refers to a robust and self-adapting framework on the basis of 2D and 3D vanilla U-Nets. We argue the strong case for taking away superfluous bells and whistles of many proposed network designs and instead focus on the remaining aspects that make out the performance and generalizability of a method. We evaluate the nnU-Net in the context of the Medical Segmentation Decathlon challenge, which measures segmentation performance in ten disciplines comprising distinct entities, image modalities, image geometries and dataset sizes, with no manual adjustments between datasets allowed. At the time of manuscript submission, nnU-Net achieves the highest mean dice scores across all classes and seven phase 1 tasks (except class 1 in BrainTumour) in the online leaderboard of the challenge.
In this paper, we focus on three problems in deep learning based medical image segmentation. Firstly, U-net, as a popular model for medical image segmentation, is difficult to train when convolutional layers increase even though a deeper network usually has a better generalization ability because of more learnable parameters. Secondly, the exponential ReLU (ELU), as an alternative of ReLU, is not much different from ReLU when the network of interest gets deep. Thirdly, the Dice loss, as one of the pervasive loss functions for medical image segmentation, is not effective when the prediction is close to ground truth and will cause oscillation during training. To address the aforementioned three problems, we propose and validate a deeper network that can fit medical image datasets that are usually small in the sample size. Meanwhile, we propose a new loss function to accelerate the learning process and a combination of different activation functions to improve the network performance. Our experimental results suggest that our network is comparable or superior to state-of-the-art methods.
Convolutional networks (ConvNets) have achieved great successes in various challenging vision tasks. However, the performance of ConvNets would degrade when encountering the domain shift. The domain adaptation is more significant while challenging in the field of biomedical image analysis, where cross-modality data have largely different distributions. Given that annotating the medical data is especially expensive, the supervised transfer learning approaches are not quite optimal. In this paper, we propose an unsupervised domain adaptation framework with adversarial learning for cross-modality biomedical image segmentations. Specifically, our model is based on a dilated fully convolutional network for pixel-wise prediction. Moreover, we build a plug-and-play domain adaptation module (DAM) to map the target input to features which are aligned with source domain feature space. A domain critic module (DCM) is set up for discriminating the feature space of both domains. We optimize the DAM and DCM via an adversarial loss without using any target domain label. Our proposed method is validated by adapting a ConvNet trained with MRI images to unpaired CT data for cardiac structures segmentations, and achieved very promising results.

Recent advances in 3D fully convolutional networks (FCN) have made it feasible to produce dense voxel-wise predictions of volumetric images. In this work, we show that a multi-class 3D FCN trained on manually labeled CT scans of several anatomical structures (ranging from the large organs to thin vessels) can achieve competitive segmentation results, while avoiding the need for handcrafting features or training class-specific models. To this end, we propose a two-stage, coarse-to-fine approach that will first use a 3D FCN to roughly define a candidate region, which will then be used as input to a second 3D FCN. This reduces the number of voxels the second FCN has to classify to ~10% and allows it to focus on more detailed segmentation of the organs and vessels. We utilize training and validation sets consisting of 331 clinical CT images and test our models on a completely unseen data collection acquired at a different hospital that includes 150 CT scans, targeting three anatomical organs (liver, spleen, and pancreas). In challenging organs such as the pancreas, our cascaded approach improves the mean Dice score from 68.5 to 82.2%, achieving the highest reported average score on this dataset. We compare with a 2D FCN method on a separate dataset of 240 CT scans with 18 classes and achieve a significantly higher performance in small organs and vessels. Furthermore, we explore fine-tuning our models to different datasets. Our experiments illustrate the promise and robustness of current 3D FCN based semantic segmentation of medical images, achieving state-of-the-art results. Our code and trained models are available for download: //github.com/holgerroth/3Dunet_abdomen_cascade.