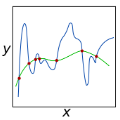
The Multiscale Hierarchical Decomposition Method (MHDM) was introduced as an iterative method for total variation regularization, with the aim of recovering details at various scales from images corrupted by additive or multiplicative noise. Given its success beyond image restoration, we extend the MHDM iterates in order to solve larger classes of linear ill-posed problems in Banach spaces. Thus, we define the MHDM for more general convex or even non-convex penalties, and provide convergence results for the data fidelity term. We also propose a flexible version of the method using adaptive convex functionals for regularization, and show an interesting multiscale decomposition of the data. This decomposition result is highlighted for the Bregman iteration method that can be expressed as an adaptive MHDM. Furthermore, we state necessary and sufficient conditions when the MHDM iteration agrees with the variational Tikhonov regularization, which is the case, for instance, for one-dimensional total variation denoising. Finally, we investigate several particular instances and perform numerical experiments that point out the robust behavior of the MHDM.
相關內容
We present NCCSG, a nonsmooth optimization method. In each iteration, NCCSG finds the best length-constrained descent direction by considering the worst bound over all local subgradients. NCCSG can take advantage of local smoothness or local strong convexity of the objective function. We prove a few global convergence rates of NCCSG. For well-behaved nonsmooth functions (characterized by the weak smooth property), NCCSG converges in $O(\frac{1}{\epsilon} \log \frac{1}{\epsilon})$ iterations, where $\epsilon$ is the desired optimality gap. For smooth functions and strongly-convex smooth functions, NCCSG achieves the lower bound of convergence rates of blackbox first-order methods, i.e., $O(\frac{1}{\epsilon})$ for smooth functions and $O(\log \frac{1}{\epsilon})$ for strongly-convex smooth functions. The efficiency of NCCSG depends on the efficiency of solving a minimax optimization problem involving the subdifferential of the objective function in each iteration.
The consistency of the maximum likelihood estimator for mixtures of elliptically-symmetric distributions for estimating its population version is shown, where the underlying distribution $P$ is nonparametric and does not necessarily belong to the class of mixtures on which the estimator is based. In a situation where $P$ is a mixture of well enough separated but nonparametric distributions it is shown that the components of the population version of the estimator correspond to the well separated components of $P$. This provides some theoretical justification for the use of such estimators for cluster analysis in case that $P$ has well separated subpopulations even if these subpopulations differ from what the mixture model assumes.
We investigate the use of multilevel Monte Carlo (MLMC) methods for estimating the expectation of discretized random fields. Specifically, we consider a setting in which the input and output vectors of the numerical simulators have inconsistent dimensions across the multilevel hierarchy. This requires the introduction of grid transfer operators borrowed from multigrid methods. Starting from a simple 1D illustration, we demonstrate numerically that the resulting MLMC estimator deteriorates the estimation of high-frequency components of the discretized expectation field compared to a Monte Carlo (MC) estimator. By adapting mathematical tools initially developed for multigrid methods, we perform a theoretical spectral analysis of the MLMC estimator of the expectation of discretized random fields, in the specific case of linear, symmetric and circulant simulators. This analysis provides a spectral decomposition of the variance into contributions associated with each scale component of the discretized field. We then propose improved MLMC estimators using a filtering mechanism similar to the smoothing process of multigrid methods. The filtering operators improve the estimation of both the small- and large-scale components of the variance, resulting in a reduction of the total variance of the estimator. These improvements are quantified for the specific class of simulators considered in our spectral analysis. The resulting filtered MLMC (F-MLMC) estimator is applied to the problem of estimating the discretized variance field of a diffusion-based covariance operator, which amounts to estimating the expectation of a discretized random field. The numerical experiments support the conclusions of the theoretical analysis even with non-linear simulators, and demonstrate the improvements brought by the proposed F-MLMC estimator compared to both a crude MC and an unfiltered MLMC estimator.
It is well known that artificial neural networks initialized from independent and identically distributed priors converge to Gaussian processes in the limit of large number of neurons per hidden layer. In this work we prove an analogous result for Quantum Neural Networks (QNNs). Namely, we show that the outputs of certain models based on Haar random unitary or orthogonal deep QNNs converge to Gaussian processes in the limit of large Hilbert space dimension $d$. The derivation of this result is more nuanced than in the classical case due to the role played by the input states, the measurement observable, and the fact that the entries of unitary matrices are not independent. An important consequence of our analysis is that the ensuing Gaussian processes cannot be used to efficiently predict the outputs of the QNN via Bayesian statistics. Furthermore, our theorems imply that the concentration of measure phenomenon in Haar random QNNs is worse than previously thought, as we prove that expectation values and gradients concentrate as $\mathcal{O}\left(\frac{1}{e^d \sqrt{d}}\right)$. Finally, we discuss how our results improve our understanding of concentration in $t$-designs.
Generalized linear models (GLMs) are routinely used for modeling relationships between a response variable and a set of covariates. The simple form of a GLM comes with easy interpretability, but also leads to concerns about model misspecification impacting inferential conclusions. A popular semi-parametric solution adopted in the frequentist literature is quasi-likelihood, which improves robustness by only requiring correct specification of the first two moments. We develop a robust approach to Bayesian inference in GLMs through quasi-posterior distributions. We show that quasi-posteriors provide a coherent generalized Bayes inference method, while also approximating so-called coarsened posteriors. In so doing, we obtain new insights into the choice of coarsening parameter. Asymptotically, the quasi-posterior converges in total variation to a normal distribution and has important connections with the loss-likelihood bootstrap posterior. We demonstrate that it is also well-calibrated in terms of frequentist coverage. Moreover, the loss-scale parameter has a clear interpretation as a dispersion, and this leads to a consolidated method of moments estimator.
The Business Process Modeling Notation (BPMN) is a widely used standard notation for defining intra- and inter-organizational workflows. However, the informal description of the BPMN execution semantics leads to different interpretations of BPMN elements and difficulties in checking behavioral properties. In this article, we propose a formalization of the execution semantics of BPMN that, compared to existing approaches, covers more BPMN elements while also facilitating property checking. Our approach is based on a higher-order transformation from BPMN models to graph transformation systems. To show the capabilities of our approach, we implemented it as an open-source web-based tool. A demonstration of our tool is available at //youtu.be/MxXbNUl6IjE.
This study investigates the potential of automated deep learning to enhance the accuracy and efficiency of multi-class classification of bird vocalizations, compared against traditional manually-designed deep learning models. Using the Western Mediterranean Wetland Birds dataset, we investigated the use of AutoKeras, an automated machine learning framework, to automate neural architecture search and hyperparameter tuning. Comparative analysis validates our hypothesis that the AutoKeras-derived model consistently outperforms traditional models like MobileNet, ResNet50 and VGG16. Our approach and findings underscore the transformative potential of automated deep learning for advancing bioacoustics research and models. In fact, the automated techniques eliminate the need for manual feature engineering and model design while improving performance. This study illuminates best practices in sampling, evaluation and reporting to enhance reproducibility in this nascent field. All the code used is available at https: //github.com/giuliotosato/AutoKeras-bioacustic Keywords: AutoKeras; automated deep learning; audio classification; Wetlands Bird dataset; comparative analysis; bioacoustics; validation dataset; multi-class classification; spectrograms.
IMPORTANCE The response effectiveness of different large language models (LLMs) and various individuals, including medical students, graduate students, and practicing physicians, in pediatric ophthalmology consultations, has not been clearly established yet. OBJECTIVE Design a 100-question exam based on pediatric ophthalmology to evaluate the performance of LLMs in highly specialized scenarios and compare them with the performance of medical students and physicians at different levels. DESIGN, SETTING, AND PARTICIPANTS This survey study assessed three LLMs, namely ChatGPT (GPT-3.5), GPT-4, and PaLM2, were assessed alongside three human cohorts: medical students, postgraduate students, and attending physicians, in their ability to answer questions related to pediatric ophthalmology. It was conducted by administering questionnaires in the form of test papers through the LLM network interface, with the valuable participation of volunteers. MAIN OUTCOMES AND MEASURES Mean scores of LLM and humans on 100 multiple-choice questions, as well as the answer stability, correlation, and response confidence of each LLM. RESULTS GPT-4 performed comparably to attending physicians, while ChatGPT (GPT-3.5) and PaLM2 outperformed medical students but slightly trailed behind postgraduate students. Furthermore, GPT-4 exhibited greater stability and confidence when responding to inquiries compared to ChatGPT (GPT-3.5) and PaLM2. CONCLUSIONS AND RELEVANCE Our results underscore the potential for LLMs to provide medical assistance in pediatric ophthalmology and suggest significant capacity to guide the education of medical students.
Hesitant fuzzy sets are widely used in the instances of uncertainty and hesitation. The inclusion relationship is an important and foundational definition for sets. Hesitant fuzzy set, as a kind of set, needs explicit definition of inclusion relationship. Base on the hesitant fuzzy membership degree of discrete form, several kinds of inclusion relationships for hesitant fuzzy sets are proposed. And then some foundational propositions of hesitant fuzzy sets and the families of hesitant fuzzy sets are presented. Finally, some foundational propositions of hesitant fuzzy information systems with respect to parameter reductions are put forward, and an example and an algorithm are given to illustrate the processes of parameter reductions.
The goal of explainable Artificial Intelligence (XAI) is to generate human-interpretable explanations, but there are no computationally precise theories of how humans interpret AI generated explanations. The lack of theory means that validation of XAI must be done empirically, on a case-by-case basis, which prevents systematic theory-building in XAI. We propose a psychological theory of how humans draw conclusions from saliency maps, the most common form of XAI explanation, which for the first time allows for precise prediction of explainee inference conditioned on explanation. Our theory posits that absent explanation humans expect the AI to make similar decisions to themselves, and that they interpret an explanation by comparison to the explanations they themselves would give. Comparison is formalized via Shepard's universal law of generalization in a similarity space, a classic theory from cognitive science. A pre-registered user study on AI image classifications with saliency map explanations demonstrate that our theory quantitatively matches participants' predictions of the AI.