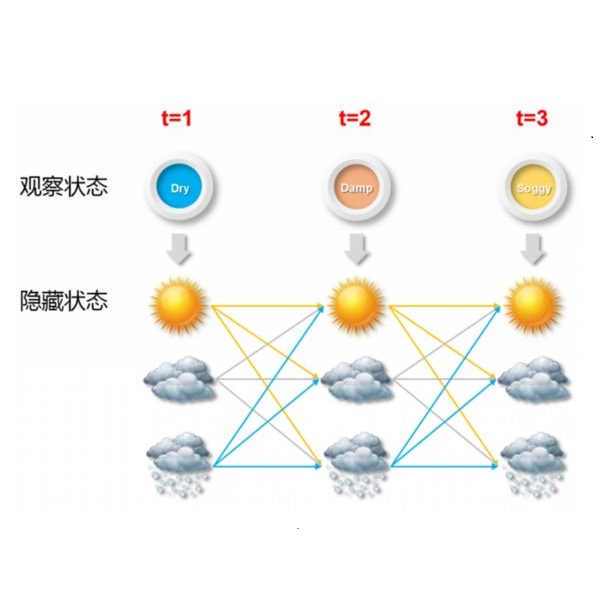
The identification of factors associated with mental and behavioral disorders in early childhood is critical both for psychopathology research and the support of primary health care practices. Motivated by the Millennium Cohort Study, in this paper we study the effect of a comprehensive set of covariates on children's emotional and behavioural trajectories in England. To this end, we develop a Quantile Mixed Hidden Markov Model for joint estimation of multiple quantiles in a linear regression setting for multivariate longitudinal data. The novelty of the proposed approach is based on the Multivariate Asymmetric Laplace distribution which allows to jointly estimate the quantiles of the univariate conditional distributions of a multivariate response, accounting for possible correlation between the outcomes. Sources of unobserved heterogeneity and serial dependency due to repeated measures are modeled through the introduction of individual-specific, time-constant random coefficients and time-varying parameters evolving over time with a Markovian structure, respectively. The inferential approach is carried out through the construction of a suitable Expectation-Maximization algorithm without parametric assumptions on the random effects distribution.
相關內容
The presence of measurement error is a widespread issue which, when ignored, can render the results of an analysis unreliable. Numerous corrections for the effects of measurement error have been proposed and studied, often under the assumption of a normally distributed, additive measurement error model. One such correction is the simulation extrapolation method, which provides a flexible way of correcting for the effects of error in a wide variety of models, when the errors are approximately normally distributed. However, in many situations observed data are non-symmetric, heavy-tailed, or otherwise highly non-normal. In these settings, correction techniques relying on the assumption of normality are undesirable. We propose an extension to the simulation extrapolation method which is nonparametric in the sense that no specific distributional assumptions are required on the error terms. The technique is implemented when either validation data or replicate measurements are available, and it shares the general structure of the standard simulation extrapolation procedure, making it immediately accessible for those familiar with this technique.
This work studies the behavior of shallow ReLU networks trained with the logistic loss via gradient descent on binary classification data where the underlying data distribution is general, and the (optimal) Bayes risk is not necessarily zero. In this setting, it is shown that gradient descent with early stopping achieves population risk arbitrarily close to optimal in terms of not just logistic and misclassification losses, but also in terms of calibration, meaning the sigmoid mapping of its outputs approximates the true underlying conditional distribution arbitrarily finely. Moreover, the necessary iteration, sample, and architectural complexities of this analysis all scale naturally with a certain complexity measure of the true conditional model. Lastly, while it is not shown that early stopping is necessary, it is shown that any univariate classifier satisfying a local interpolation property is inconsistent.
Stratifying factors, like age and gender, can modify the effect of treatments and exposures on risk of a studied outcome. Several effect measures, including the relative risk, hazard ratio, odds ratio, and risk difference, can be used to measure this modification. It is known that choice of effect measure may determine the presence and direction of effect-measure modification. We show that considering the opposite outcome -- for example, recovery instead of death -- may similarly influence effect-measure modification. In fact, if the relative risk for the studied outcome and the relative risk for the opposite outcome agree about the direction of effect-measure modification, then so will the two cumulative hazard ratios, the risk difference, and the odds ratio. When risks are randomly sampled from the uniform (0,1) distribution, the probability of this happening is 5/6. Disagreement is probable enough that researchers considering one relative risk should also consider the other and further discussion if they disagree. (If possible, researchers should also report estimated risks.) We provide examples through case studies on HCV, COVID-19, and bankruptcy following melanoma treatment.
Quantification of microbial interactions from 16S rRNA and meta-genomic sequencing data is difficult due to their sparse nature, as well as the fact that the data only provides measures of relative abundance. In this paper, we propose using copula models with mixed zero-beta margins for estimation of taxon-taxon interactions using the normalized microbial relative abundances. Copulas allow for separate modeling of the dependence structure from the margins, marginal covariate adjustment, and uncertainty measurement. Our method shows that a two-stage maximum likelihood approach provides accurate estimation of the model parameters. A corresponding two-stage likelihood-ratio test for the dependence parameter is derived. Simulation studies show that the test is valid and more powerful than tests based upon Pearson's and rank correlations. Furthermore, we demonstrate that our method can be used to build biologically meaningful microbial networks based on the data set of the American Gut Project.
In embryogenesis, epithelial cells, acting as individual entities or as coordinated aggregates in a tissue, exhibit strong coupling between chemical signalling and mechanical responses to internally or externally applied stresses. Intercellular communication in combination with such coordination of morphogenetic movements can lead to drastic modifications in the calcium distribution in the cells. In this paper we extend the recent mechanochemical model in [K. Kaouri, P.K. Maini, P.A. Skourides, N. Christodoulou, S.J. Chapman. J. Math. Biol., 78 (2019) 2059--2092], for an epithelial continuum in one dimension, to a more realistic multi-dimensional case. The resulting parametrised governing equations consist of an advection-diffusion-reaction system for calcium signalling coupled with active-stress linear viscoelasticity and equipped with pure Neumann boundary conditions. We implement a mixed finite element method for the simulation of this complex multiphysics problem. Special care is taken in the treatment of the stress-free boundary conditions for the viscoelasticity in order to eliminate rigid motions from the space of admissible displacements. The stability and solvability of the continuous weak formulation is shown using fixed-point theory. We investigate numerically the solutions of this system and show that solitary waves and periodic wavetrains of calcium propagate through the embryonic epithelial sheet. We analyse the bifurcations of the system guided by the bifurcation analysis of the one-dimensional model. We also demonstrate the nucleation of calcium sparks into synchronous calcium waves coupled with contraction. This coupled model can be employed to gain insights into recent experimental observations in the context of embryogenesis, but also in other biological systems such as cancer cells, wound healing, keratinocytes, or white blood cells.
Gaussian process (GP) models that combine both categorical and continuous input variables have found use e.g. in longitudinal data analysis and computer experiments. However, standard inference for these models has the typical cubic scaling, and common scalable approximation schemes for GPs cannot be applied since the covariance function is non-continuous. In this work, we derive a basis function approximation scheme for mixed-domain covariance functions, which scales linearly with respect to the number of observations and total number of basis functions. The proposed approach is naturally applicable to Bayesian GP regression with arbitrary observation models. We demonstrate the approach in a longitudinal data modelling context and show that it approximates the exact GP model accurately, requiring only a fraction of the runtime compared to fitting the corresponding exact model.
Phase-type (PH) distributions are a popular tool for the analysis of univariate risks in numerous actuarial applications. Their multivariate counterparts (MPH$^\ast$), however, have not seen such a proliferation, due to lack of explicit formulas and complicated estimation procedures. A simple construction of multivariate phase-type distributions -- mPH -- is proposed for the parametric description of multivariate risks, leading to models of considerable probabilistic flexibility and statistical tractability. The main idea is to start different Markov processes at the same state, and allow them to evolve independently thereafter, leading to dependent absorption times. By dimension augmentation arguments, this construction can be cast into the umbrella of MPH$^\ast$ class, but enjoys explicit formulas which the general specification lacks, including common measures of dependence. Moreover, it is shown that the class is still rich enough to be dense on the set of multivariate risks supported on the positive orthant, and it is the smallest known sub-class to have this property. In particular, the latter result provides a new short proof of the denseness of the MPH$^\ast$ class. In practice this means that the mPH class allows for modeling of bivariate risks with any given correlation or copula. We derive an EM algorithm for its statistical estimation, and illustrate it on bivariate insurance data. Extensions to more general settings are outlined.
Normalizing flows are invertible neural networks with tractable change-of-volume terms, which allow optimization of their parameters to be efficiently performed via maximum likelihood. However, data of interest are typically assumed to live in some (often unknown) low-dimensional manifold embedded in a high-dimensional ambient space. The result is a modelling mismatch since -- by construction -- the invertibility requirement implies high-dimensional support of the learned distribution. Injective flows, mappings from low- to high-dimensional spaces, aim to fix this discrepancy by learning distributions on manifolds, but the resulting volume-change term becomes more challenging to evaluate. Current approaches either avoid computing this term entirely using various heuristics, or assume the manifold is known beforehand and therefore are not widely applicable. Instead, we propose two methods to tractably calculate the gradient of this term with respect to the parameters of the model, relying on careful use of automatic differentiation and techniques from numerical linear algebra. Both approaches perform end-to-end nonlinear manifold learning and density estimation for data projected onto this manifold. We study the trade-offs between our proposed methods, empirically verify that we outperform approaches ignoring the volume-change term by more accurately learning manifolds and the corresponding distributions on them, and show promising results on out-of-distribution detection. Our code is available at //github.com/layer6ai-labs/rectangular-flows.
We introduce a flexible and scalable class of Bayesian geostatistical models for discrete data, based on the class of nearest neighbor mixture transition distribution processes (NNMP), referred to as discrete NNMP. The proposed class characterizes spatial variability by a weighted combination of first-order conditional probability mass functions (pmfs) for each one of a given number of neighbors. The approach supports flexible modeling for multivariate dependence through specification of general bivariate discrete distributions that define the conditional pmfs. Moreover, the discrete NNMP allows for construction of models given a pre-specified family of marginal distributions that can vary in space, facilitating covariate inclusion. In particular, we develop a modeling and inferential framework for copula-based NNMPs that can attain flexible dependence structures, motivating the use of bivariate copula families for spatial processes. Compared to the traditional class of spatial generalized linear mixed models, where spatial dependence is introduced through a transformation of response means, our process-based modeling approach provides both computational and inferential advantages. We illustrate the benefits with synthetic data examples and an analysis of North American Breeding Bird Survey data.
Long Short-Term Memory (LSTM) infers the long term dependency through a cell state maintained by the input and the forget gate structures, which models a gate output as a value in [0,1] through a sigmoid function. However, due to the graduality of the sigmoid function, the sigmoid gate is not flexible in representing multi-modality or skewness. Besides, the previous models lack modeling on the correlation between the gates, which would be a new method to adopt inductive bias for a relationship between previous and current input. This paper proposes a new gate structure with the bivariate Beta distribution. The proposed gate structure enables probabilistic modeling on the gates within the LSTM cell so that the modelers can customize the cell state flow with priors and distributions. Moreover, we theoretically show the higher upper bound of the gradient compared to the sigmoid function, and we empirically observed that the bivariate Beta distribution gate structure provides higher gradient values in training. We demonstrate the effectiveness of bivariate Beta gate structure on the sentence classification, image classification, polyphonic music modeling, and image caption generation.