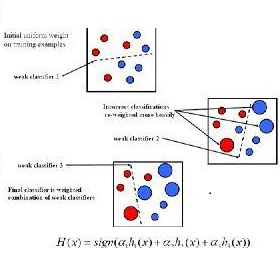
AdaBoost is one of the most popular ML algorithms. It is simple to implement and often found very effective by practitioners, while still being mathematically elegant and theoretically sound. AdaBoost's interesting behavior in practice still puzzles the ML community. We address the algorithm's stability and establish multiple convergence properties of "Optimal AdaBoost," a term coined by Rudin, Daubechies, and Schapire in 2004. We prove, in a reasonably strong computational sense, the almost universal existence of time averages, and with that, the convergence of the classifier itself, its generalization error, and its resulting margins, among many other objects, for fixed data sets under arguably reasonable conditions. Specifically, we frame Optimal AdaBoost as a dynamical system and, employing tools from ergodic theory, prove that, under a condition that Optimal AdaBoost does not have ties for best weak classifier eventually, a condition for which we provide empirical evidence from high dimensional real-world datasets, the algorithm's update behaves like a continuous map. We provide constructive proofs of several arbitrarily accurate approximations of Optimal AdaBoost; prove that they exhibit certain cycling behavior in finite time, and that the resulting dynamical system is ergodic; and establish sufficient conditions for the same to hold for the actual Optimal-AdaBoost update. We believe that our results provide reasonably strong evidence for the affirmative answer to two open conjectures, at least from a broad computational-theory perspective: AdaBoost always cycles and is an ergodic dynamical system. We present empirical evidence that cycles are hard to detect while time averages stabilize quickly. Our results ground future convergence-rate analysis and may help optimize generalization ability and alleviate a practitioner's burden of deciding how long to run the algorithm.
相關內容
Diagnosing convergence of Markov chain Monte Carlo is crucial and remains an essentially unsolved problem. Among the most popular methods, the potential scale reduction factor, commonly named $\hat{R}$, is an indicator that monitors the convergence of output chains to a target distribution, based on a comparison of the between- and within-variances. Several improvements have been suggested since its introduction in the 90s. Here, we aim at better understanding the $\hat{R}$ behavior by proposing a localized version that focuses on quantiles of the target distribution. This new version relies on key theoretical properties of the associated population value. It naturally leads to proposing a new indicator $\hat{R}_\infty$, which is shown to allow both for localizing the Markov chain Monte Carlo convergence in different quantiles of the target distribution, and at the same time for handling some convergence issues not detected by other $\hat{R}$ versions.
While the empirical success of self-supervised learning (SSL) heavily relies on the usage of deep nonlinear models, existing theoretical works on SSL understanding still focus on linear ones. In this paper, we study the role of nonlinearity in the training dynamics of contrastive learning (CL) on one and two-layer nonlinear networks with homogeneous activation $h(x) = h'(x)x$. We have two major theoretical discoveries. First, the presence of nonlinearity can lead to many local optima even in 1-layer setting, each corresponding to certain patterns from the data distribution, while with linear activation, only one major pattern can be learned. This suggests that models with lots of parameters can be regarded as a \emph{brute-force} way to find these local optima induced by nonlinearity. Second, in the 2-layer case, linear activation is proven not capable of learning specialized weights into diverse patterns, demonstrating the importance of nonlinearity. In addition, for 2-layer setting, we also discover \emph{global modulation}: those local patterns discriminative from the perspective of global-level patterns are prioritized to learn, further characterizing the learning process. Simulation verifies our theoretical findings.
Mathematical models are essential for understanding and making predictions about systems arising in nature and engineering. Yet, mathematical models are a simplification of true phenomena, thus making predictions subject to uncertainty. Hence, the ability to quantify uncertainties is essential to any modelling framework, enabling the user to assess the importance of certain parameters on quantities of interest and have control over the quality of the model output by providing a rigorous understanding of uncertainty. Peridynamic models are a particular class of mathematical models that have proven to be remarkably accurate and robust for a large class of material failure problems. However, the high computational expense of peridynamic models remains a major limitation, hindering outer-loop applications that require a large number of simulations, for example, uncertainty quantification. This contribution provides a framework to make such computations feasible. By employing a Multilevel Monte Carlo (MLMC) framework, where the majority of simulations are performed using a coarse mesh, and performing relatively few simulations using a fine mesh, a significant reduction in computational cost can be realised, and statistics of structural failure can be estimated. The results show a speed-up factor of 16x over a standard Monte Carlo estimator, enabling the forward propagation of uncertain parameters in a computationally expensive peridynamic model. Furthermore, the multilevel method provides an estimate of both the discretisation error and sampling error, thus improving the confidence in numerical predictions. The performance of the approach is demonstrated through an examination of the statistical size effect in quasi-brittle materials.
Bayesian persuasion studies how an informed sender should influence beliefs of rational receivers who take decisions through Bayesian updating of a common prior. We focus on the online Bayesian persuasion framework, in which the sender repeatedly faces one or more receivers with unknown and adversarially selected types. First, we show how to obtain a tight $\tilde O(T^{1/2})$ regret bound in the case in which the sender faces a single receiver and has partial feedback, improving over the best previously known bound of $\tilde O(T^{4/5})$. Then, we provide the first no-regret guarantees for the multi-receiver setting under partial feedback. Finally, we show how to design no-regret algorithms with polynomial per-iteration running time by exploiting type reporting, thereby circumventing known intractability results on online Bayesian persuasion. We provide efficient algorithms guaranteeing a $O(T^{1/2})$ regret upper bound both in the single- and multi-receiver scenario when type reporting is allowed.
We study the secretary problem in which rank-ordered lists are generated by the Mallows model and the goal is to identify the highest-ranked candidate through a sequential interview process which does not allow rejected candidates to be revisited. The main difference between our formulation and existing models is that, during the selection process, we are given a fixed number of opportunities to query an infallible expert whether the current candidate is the highest-ranked or not. If the response is positive, the selection process terminates, otherwise, the search continues until a new potentially optimal candidate is identified. Our optimal interview strategy, as well as the expected number of candidates interviewed and the expected number of queries used, can be determined through the evaluation of well-defined recurrence relations. Specifically, if we are allowed to query $s-1$ times and to make a final selection without querying (thus, making $s$ selections in total) then the optimum scheme is characterized by $s$ thresholds that depend on the parameter $\theta$ of the Mallows distribution but are independent on the maximum number of queries.
Modern clinical and epidemiological studies widely employ wearables to record parallel streams of real-time data on human physiology and behavior. With recent advances in distributional data analysis, these high-frequency data are now often treated as distributional observations resulting in novel regression settings. Motivated by these modelling setups, we develop a distributional outcome regression via quantile functions (DORQF) that expands existing literature with three key contributions: i) handling both scalar and distributional predictors, ii) ensuring jointly monotone regression structure without enforcing monotonicity on individual functional regression coefficients, iii) providing statistical inference via asymptotic projection-based joint confidence bands and a statistical test of global significance to quantify uncertainty of the estimated functional regression coefficients. The method is motivated by and applied to Actiheart component of Baltimore Longitudinal Study of Aging that collected one week of minute-level heart rate (HR) and physical activity (PA) data on 781 older adults to gain deeper understanding of age-related changes in daily life heart rate reserve, defined as a distribution of daily HR, while accounting for daily distribution of physical activity, age, gender, and body composition. Intriguingly, the results provide novel insights in epidemiology of daily life heart rate reserve.
Ensemble sampling serves as a practical approximation to Thompson sampling when maintaining an exact posterior distribution over model parameters is computationally intractable. In this paper, we establish a regret bound that ensures desirable behavior when ensemble sampling is applied to the linear bandit problem. This represents the first rigorous regret analysis of ensemble sampling and is made possible by leveraging information-theoretic concepts and novel analytic techniques that may prove useful beyond the scope of this paper.
For the stochastic heat equation with multiplicative noise we consider the problem of estimating the diffusivity parameter in front of the Laplace operator. Based on local observations in space, we first study an estimator that was derived for additive noise. A stable central limit theorem shows that this estimator is consistent and asymptotically mixed normal. By taking into account the quadratic variation, we propose two new estimators. Their limiting distributions exhibit a smaller (conditional) variance and the last estimator also works for vanishing noise levels. The proofs are based on local approximation results to overcome the intricate nonlinearities and on a stable central limit theorem for stochastic integrals with respect to cylindrical Brownian motion. Simulation results illustrate the theoretical findings.
We introduce the Weak-form Estimation of Nonlinear Dynamics (WENDy) method for estimating model parameters for non-linear systems of ODEs. The core mathematical idea involves an efficient conversion of the strong form representation of a model to its weak form, and then solving a regression problem to perform parameter inference. The core statistical idea rests on the Errors-In-Variables framework, which necessitates the use of the iteratively reweighted least squares algorithm. Further improvements are obtained by using orthonormal test functions, created from a set of $C^{\infty}$ bump functions of varying support sizes. We demonstrate that WENDy is a highly robust and efficient method for parameter inference in differential equations. Without relying on any numerical differential equation solvers, WENDy computes accurate estimates and is robust to large (biologically relevant) levels of measurement noise. For low dimensional systems with modest amounts of data, WENDy is competitive with conventional forward solver-based nonlinear least squares methods in terms of speed and accuracy. For both higher dimensional systems and stiff systems, WENDy is typically both faster (often by orders of magnitude) and more accurate than forward solver-based approaches. We illustrate the method and its performance in some common population and neuroscience models, including logistic growth, Lotka-Volterra, FitzHugh-Nagumo, Hindmarsh-Rose, and a Protein Transduction Benchmark model. Software and code for reproducing the examples is available at (//github.com/MathBioCU/WENDy).
Residual networks (ResNets) have displayed impressive results in pattern recognition and, recently, have garnered considerable theoretical interest due to a perceived link with neural ordinary differential equations (neural ODEs). This link relies on the convergence of network weights to a smooth function as the number of layers increases. We investigate the properties of weights trained by stochastic gradient descent and their scaling with network depth through detailed numerical experiments. We observe the existence of scaling regimes markedly different from those assumed in neural ODE literature. Depending on certain features of the network architecture, such as the smoothness of the activation function, one may obtain an alternative ODE limit, a stochastic differential equation or neither of these. These findings cast doubts on the validity of the neural ODE model as an adequate asymptotic description of deep ResNets and point to an alternative class of differential equations as a better description of the deep network limit.